2020-2021学年第9章 中心对称图形——平行四边形9.2 中心对称与中心对称图形课后测评

这是一份2020-2021学年第9章 中心对称图形——平行四边形9.2 中心对称与中心对称图形课后测评，文件包含专题92中心对称与中心对称图形-2021-2022学年八年级数学下册尖子生同步培优题典解析版苏科版docx、专题92中心对称与中心对称图形-2021-2022学年八年级数学下册尖子生同步培优题典原卷版苏科版docx等2份试卷配套教学资源，其中试卷共26页， 欢迎下载使用。

2021-2022学年八年级数学下册尖子生同步培优题典【苏科版】
专题9.2中心对称与中心对称图形
姓名：__________________ 班级：______________ 得分：_________________
注意事项：
本试卷满分100分，试题共24题，选择10道、填空8道、解答6道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．
一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．
1．（2020秋•邗江区期中）下列图形中既是轴对称图形，又是中心对称图形的是（　　）
A． B．
C． D．
【分析】根据中心对称图形的定义判断，得到答案．
【解析】A、既是轴对称图形，又是中心对称图形，故本选项符合题意；
B、是轴对称图形，不是中心对称图形，故本选项不符合题意；
C、是轴对称图形，不是中心对称图形，故本选项不符合题意；
D、是轴对称图形，不是中心对称图形，故本选项不符合题意；
故选：A．
2．（2020春•工业园区校级期中）下列图标中，是中心对称图形的是（　　）
A． B． C． D．
【分析】根据中心对称图形的概念判断即可．
【解析】A、不属于中心对称图形；
B、属于中心对称图形；
C、不属于中心对称图形；
D、不属于中心对称图形；
故选：B．
3．（2020春•仪征市期中）在线段、角、等腰三角形、平行四边形、矩形、菱形这几个图形中是中心对称图形的个数是（　　）
A．2个 B．3个 C．4个 D．5个
【分析】把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，据此进行判断即可．
【解析】由题可得，中心对称图形的有：线段、平行四边形、矩形、菱形共4个．
故选：C．
4．（2020春•相城区期末）如图，菱形ABCD的对角线AC、BD交于点O，AC＝4，BD＝16，将△BOC绕着点C旋转180°得到△B′O′C，则点A与点B′之间的距离为（　　）

A．6 B．8 C．10 D．12
【分析】根据菱形ABCD的对角线AC、BD交于点O，AC＝4，BD＝16，可得AC⊥BD，所以∠BOC＝90°，根据△BOC绕着点C旋转180°得到△B′O′C，所以∠CO′B′＝∠BOC＝90°，AO′＝6，OB′＝8，再根据勾股定理即可求出点A与点B′之间的距离．
【解析】∵菱形ABCD的对角线AC、BD交于点O，AC＝4，BD＝16，
∴AC⊥BD，
∴∠BOC＝90°，
∵△BOC绕着点C旋转180°得到△B′O′C，
∴∠CO′B′＝∠BOC＝90°，
∴O′C＝OC＝OA=12AC＝2，
∴AO′＝6，
∵OB＝OD＝OB′=12BD＝8，
在Rt△AO′B′中，根据勾股定理，得
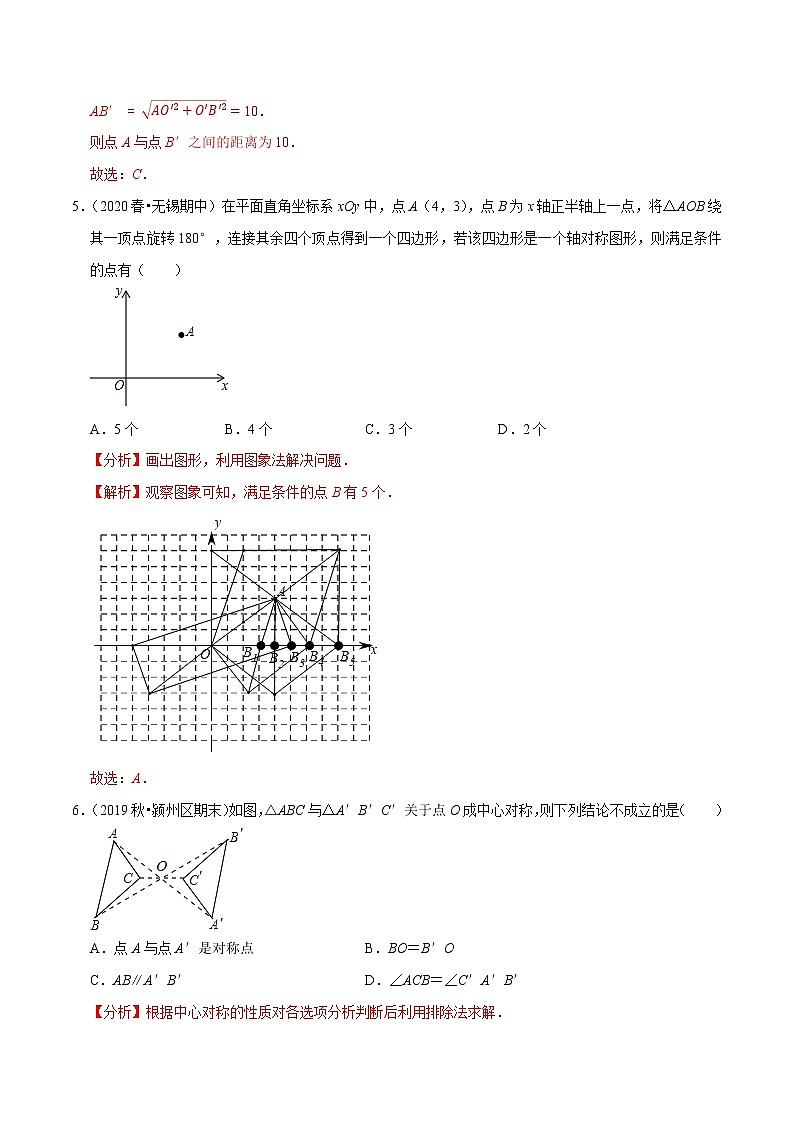
AB′=AO'2+O'B'2=10．
则点A与点B′之间的距离为10．
故选：C．
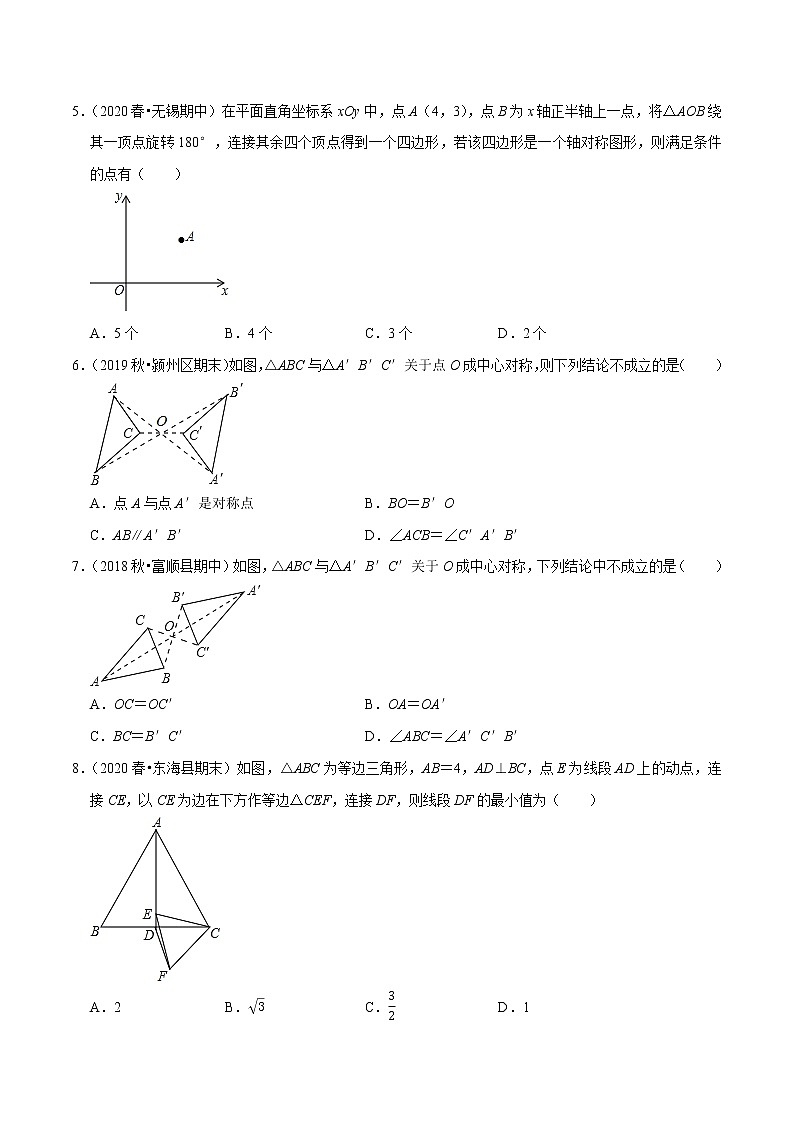
5．（2020春•无锡期中）在平面直角坐标系xOy中，点A（4，3），点B为x轴正半轴上一点，将△AOB绕其一顶点旋转180°，连接其余四个顶点得到一个四边形，若该四边形是一个轴对称图形，则满足条件的点有（　　）

A．5个 B．4个 C．3个 D．2个
【分析】画出图形，利用图象法解决问题．
【解析】观察图象可知，满足条件的点B有5个．

故选：A．
6．（2019秋•颍州区期末）如图，△ABC与△A′B′C′关于点O成中心对称，则下列结论不成立的是（　　）

A．点A与点A′是对称点 B．BO＝B′O
C．AB∥A′B′ D．∠ACB＝∠C′A′B′
【分析】根据中心对称的性质对各选项分析判断后利用排除法求解．
【解析】观察图形可知，
A、点A与点A′是对称点，故本选项正确；
B、BO＝B′O，故本选项正确；
C、AB∥A′B′，故本选项正确；
D、∠ACB＝∠A′C′B′，故本选项错误．
故选：D．
7．（2018秋•富顺县期中）如图，△ABC与△A′B′C′关于O成中心对称，下列结论中不成立的是（　　）

A．OC＝OC′ B．OA＝OA′
C．BC＝B′C′ D．∠ABC＝∠A′C′B′
【分析】根据中心对称的性质即可判断．
【解析】对应点的连线被对称中心平分，A，B正确；
成中心对称图形的两个图形是全等形，那么对应线段相等，C正确．
故选：D．
8．（2020春•东海县期末）如图，△ABC为等边三角形，AB＝4，AD⊥BC，点E为线段AD上的动点，连接CE，以CE为边在下方作等边△CEF，连接DF，则线段DF的最小值为（　　）

A．2 B．3 C．32 D．1
【分析】连接BF，由等边三角形的性质可得三角形全等的条件，从而可证△BCF≌△ACE，推出∠CBF＝∠CAE＝30°，再由垂线段最短可知当DF⊥BF时，DF值最小，利用含30°的直角三角形的性质定理可求DF的值．
【解析】如图，连接BF，

∵△ABC为等边三角形，AD⊥BC，AB＝4，
∴BC＝AC＝AB＝4，BD＝DC＝2，∠BAC＝∠ACB＝60°，∠CAE＝30°，
∵△CEF为等边三角形，
∴CF＝CE，∠FCE＝60°，
∴∠FCE＝∠ACB，
∴∠BCF＝∠ACE，
∴在△BCF和△ACE中，
BC=AC∠BCF=∠ACECF=CE，
∴△BCF≌△ACE（SAS），
∴∠CBF＝∠CAE＝30°，AE＝BF，
∴当DF⊥BF时，DF值最小，
此时∠BFD＝90°，∠CBF＝30°，BD＝2，
∴DF＝1，
故选：D．
9．（2020春•曹县期末）如图，将△ABC绕点C顺时针旋转得到△DEC，使点A的对应点D恰好落在边AB上，点B的对应点为E，连接BE，下列结论正确的是（　　）

A．AC＝AD B．BC＝DE C．AB⊥EB D．∠A＝∠EBC
【分析】根据旋转的性质得到AC＝CD，BC＝CE，AB＝DE，故A错误，B错误；可得出∠ACD＝∠BCE，根据三角形的内角和得到∠A＝∠ADC=180°−∠ACD2，∠CBE=180°−∠BCE2，求得∠A＝∠EBC，故D正确；由于∠A+∠ABC不一定等于90°，于是得到∠ABC+∠CBE不一定等于90°，故C错误．
【解析】∵将△ABC绕点C顺时针旋转得到△DEC，
∴AC＝CD，BC＝CE，AB＝DE，故A错误，B错误；
∴∠ACD＝∠BCE，
∴∠A＝∠ADC=180°−∠ACD2，∠CBE=180°−∠BCE2，
∴∠A＝∠EBC，故D正确；
∵∠A+∠ABC不一定等于90°，
∴∠ABC+∠CBE不一定等于90°，故C错误．
故选：D．
10．（2020春•江阴市校级期中）如图，在Rt△ABC中，∠C＝90°，把△ABC绕AC边的中点M旋转后得△DEF，若直角顶点F恰好落在AB边上，且DE边交AB边于点G，若AC＝4，BC＝3，则AG的长为（　　）

A．710 B．34 C．45 D．1
【分析】根据勾股定理得到AB＝5，得到CM＝AM=12AC＝2，根据旋转的性质得到CM＝FM＝2，∠D＝∠A，∠C＝∠DFE，AB＝DE，求得AM＝MF，求得FG=12DE=52，根据勾股定理即可得到结论．
【解析】∵在Rt△ABC中，∠C＝90°，AC＝4，BC＝3，
∴AB＝5，
∵点M是AC边的中点，
∴CM＝AM=12AC＝2，
∵把△ABC绕AC边的中点M旋转后得△DEF，若直角顶点F恰好落在AB边上，
∴CM＝FM＝2，∠D＝∠A，∠C＝∠DFE，AB＝DE，
∴AM＝MF，
∴∠A＝∠AFM，
∴∠D＝∠AFD，
∴DG＝FG，
∵∠D+∠E＝∠DFG+∠GFE＝90°，
∴∠E＝∠EFG，
∴EG＝FG，
∴FG=12DE=52，
∵AM＝CM＝FM=12AC，
∴∠AFC＝90°，
∴CF=AC⋅BCAB=125，
∴AF=AC2−CF242−(125)2=165，
∴AG＝AF﹣FG=165−52=710，
故选：A．

二、填空题（本大题共8小题，每小题3分，共24分）请把答案直接填写在横线上
11．（2020春•江都区期中）在等腰直角三角形、等边三角形、平行四边形、矩形、菱形、正方形中，既是轴对称图形，又是中心对称图形的有　3　个．
【分析】根据轴对称图形与中心对称图形的概念求解．
【解析】由题可得，既是轴对称图形，又是中心对称图形的有3个：矩形、菱形、正方形，
故答案为：3．
12．（2020•滨湖区一模）给出如下5种图形：①矩形，②等边三角形，③正五边形，④圆，⑤线段．其中，是轴对称图形但不是中心对称图形的有　②③　．（请将所有符合题意的序号填在横线上）
【分析】根据轴对称图形与中心对称图形的概念求解．
【解析】①矩形是轴对称图形，是中心对称图形；
②等边三角形是轴对称图形，不是中心对称图形；
③正五边形是轴对称图形，不是中心对称图形；
④圆是轴对称图形，是中心对称图形；
⑤线段是轴对称图形，是中心对称图形；
则是轴对称图形但不是中心对称图形的②③，
故答案为：②③．
13．（2019春•丹阳市期末）下列4种图案中，既是轴对称图形，又是中心对称图形的有　1　个．

【分析】根据轴对称图形与中心对称图形的概念求解．
【解析】第一个图形是轴对称图形，也是中心对称图形；
第二个图形不是轴对称图形，也不是中心对称图形；
第三个图形不是轴对称图形，也不是中心对称图形；
第四个图形是轴对称图形，不是中心对称图形．
故答案为：1．
14．（2018秋•汶上县期末）六张完全相同的卡片上，分别画有等边三角形、正方形、矩形、平行四边形、圆、菱形，现从中随机抽取一张，卡片上画的恰好既是轴对称图形又是中心对称图形的概率为　23　．
【分析】根据中心对称图形与轴对称图形的概念进行判断，根据概率的公式计算．
【解析】等边三角形是轴对称图形，不是中心对称图形，
正方形是轴对称图形，也是中心对称图形，
矩形是轴对称图形，也是中心对称图形，
平行四边形不是轴对称图形，是中心对称图形，
圆是轴对称图形，也是中心对称图形，
菱形是轴对称图形，也是中心对称图形，
卡片上画的恰好既是轴对称图形又是中心对称图形的概率为46=23，
故答案为：23．
15．（2018春•泰兴市校级期中）如图，点A，B，C的坐标分别为（0，﹣1），（0，2），（3，0）．从下面四个点M（3，3），N（3，﹣3），P（﹣3，0），Q（﹣3，1）中选择一个点，以A，B，C与该点为顶点的四边形不是中心对称图形，则该点是　点P　．

【分析】根据中心对称图形的概念，只要组成的四边形不是平行四边形，则一定不是中心对称图形．
【解析】根据平行四边形的判定，已知M、N、Q都能够和已知的三个点组成平行四边形，则一定是中心对称图形．
故答案为：点P．
16．（2020秋•港口区期中）如图，将△OAB绕点O逆时针旋转70°到△OCD的位置，若∠AOB＝40°，则∠AOD的大小为　30　度．

【分析】由旋转的性质可得∠DOB＝70°，即可求解．
【解析】∵将△OAB绕点O逆时针旋转70°到△OCD，
∴∠DOB＝70°，
∵∠AOB＝40°，
∴∠AOD＝∠BOD﹣∠AOB＝30°，
故答案为：30．
17．（2020春•秦淮区期末）如图，在△ABC中，∠BAC＝90°，AB＝AC，P是△ABC内一点，若PA＝1，PC＝2，∠APC＝135°，则PB的长为　6　．

【分析】把△APC绕点A顺时针旋转90°得到△ABD，根据旋转的性质可得△APD是等腰直角三角形，AD＝AP，∠APD＝∠ADP＝45°，根据等腰直角三角形的性质求出PD，∠CPD＝180°，可得点C、P、D在同一条直线上，然后利用勾股定理求出PB的长即可．
【解析】如图，把△APC绕点A顺时针旋转90°得到△ABD，
∴AP＝AD＝1，PC＝DB＝2，∠ACP＝∠ABD，

根据旋转的性质可得△APD是等腰直角三角形，AD＝AP＝1，∠APD＝∠ADP＝45°，
∴PD=2，
∵∠APC＝135°，
∴∠APC+∠APD＝180°，
∴点C、P、D在同一条直线上，
∵∠BAC＝90°，AB＝AC，
∴∠ABC+∠ACB＝90°
∵∠ACP＝∠ABD，
∴∠DBC+∠PCB＝90°，
∴∠BDC＝90°，
∴在Rt△BDP中，根据勾股定理，得
PB=BD2+PD2=4+2=6．
故答案为：6．
18．（2020春•丹阳市期末）一副三角板按如图所示叠放在一起，∠C＝60°，∠OAB＝45°，其中点B、D重合，若固定△AOB，将三角板ACD绕着公共顶点A顺时针旋转一周后停止，当旋转角为　75°或255°　度时，CD∥AO．

【分析】分两种情形：如图1中，当CD在OA的左侧，CD∥AO时，如图2中，当CD在OA的右侧，CD∥AO时，分别求解即可．
【解析】如图1中，当CD在OA的左侧，CD∥AO时，旋转角＝45°+30°＝75°

如图2中，当CD在OA的右侧，CD∥OA时，旋转角＝45°+180°+30°＝255°，

故答案为75°或255°．
三、解答题（本大题共6小题，共46分．解答时应写出文字说明、证明过程或演算步骤）
19．（2020春•灌云县期中）如图，D是△ABC边BC的中点，连接AD并延长到点E，使DE＝AD，连接BE．
（1）图中哪两个图形成中心对称？
（2）若△ADC的面积为4，求△ABE的面积．

【分析】（1）直接利用中心对称的定义写出答案即可；
（2）根据成中心对称的图形的两个图形全等确定三角形BDE的面积，根据等底同高确定ABD的面积，从而确定ABE的面积．
【解析】（1）图中△ADC和三角形EDB成中心对称；

（2）∵△ADC和三角形EDB成中心对称，△ADC的面积为4，
∴△EDB的面积也为4，
∵D为BC的中点，
∴△ABD的面积也为4，
所以△ABE的面积为8．
20．（2019春•秦淮区期末）如图，是5个全等的小正方形组成的图案，请用不同的两种方法分别在两幅图中各添加1个正方形，使整个图案称为中心对称图形．

【分析】直接利用中心对称图形的定义进而分析得出答案．
【解析】如图所示：
．
21．（2020秋•安定区期末）如图，方格纸中每个小正方形的边长都是1个单位长度，在方格纸中建立如图所示的平面直角坐标系，△ABC的顶点都在格点上．
（1）将△ABC向右平移6个单位长度得到△A1B1C1，请画出△A1B1C1；
（2）画出△A1B1C1关于点O的中心对称图形△A2B2C2；
（3）若将△ABC绕某一点旋转可得到△A2B2C2，请直接写出旋转中心的坐标．

【分析】（1）根据平移的性质即可将△ABC向右平移6个单位长度得到△A1B1C1；
（2）根据中心对称的定义即可画出△A1B1C1关于点O的中心对称图形△A2B2C2；
（3）根据旋转的性质即可将△ABC绕某一点旋转可得到△A2B2C2，进而写出旋转中心的坐标．
【解析】（1）如图，△A1B1C1即为所求；

（2）如图，△A2B2C2即为所求；
（3）根据图形可知：
旋转中心的坐标为：（﹣3，0）．
22．（2020春•太仓市期末）如图，在12×12正方形网格中建立直角坐标系，每个小正方形的边长为1个单位长度，△ABC的三个顶点A（0，2），B（3，5），C（2，2）．
（1）将△ABC以点A为旋转中心旋转180°，得到△AB1C1，点B、C的对应点分别是点B1，C1，请在网格图中画出△AB1C1．
（2）将△ABC平移至△A2B2C2，其中点A，B，C的对应点分别为点A2，B2，C2，且点C2的坐标为（2，﹣4），请在图中画出平移后的△A2B2C2．
（3）在第（1）、（2）小题基础上，若将△AB1C1绕某一点旋转可得到△A2B2C2，则旋转中心点P的坐标为　（0，﹣1）　．（直接写出答案）

【分析】（1）根据旋转的性质可将△ABC以点A为旋转中心旋转180°，即可得到△AB1C1，点B、C的对应点分别是点B1，C1；
（2）根据点C2的坐标为（2，﹣4），即可在图中画出平移后的△A2B2C2．
（3）在第（1）、（2）小题基础上，根据旋转的性质即可将△AB1C1绕某一点旋转可得到△A2B2C2．
【解析】（1）如图，△AB1C1即为所求；

（2）如图，△A2B2C2即为所求；
（3）旋转中心点P的坐标为（0，﹣1）．
故答案为：（0，﹣1）．
23．（2020春•常州期中）如图，△AOB和△COD均为等腰直角三角形，∠AOB＝∠COD＝90°，点C、D分别在OA、OB上的点，连接AD、BC，点H为BC中点，连接OH．
（1）如图1，求证OH=12AD，OH⊥AD；
（2）将△COD绕点O旋转到图2所示位置时，（1）中结论是否仍成立？若成立，证明你的结论；若不成立，请说明理由．

【分析】（1）只要证明△AOD≌△BOC（SAS），即可解决问题；
（2）延长OH到E，使得HE＝OH，连接BE，证明△BEH≌△CHO（SAS），可得OE＝2OH，∠EBC＝∠BCO，证明△BEO≌△ODA（SAS）即可解决问题．
【解析】（1）证明：∵△OAB与△OCD为等腰直角三角形，∠AOB＝∠COD＝90°，
∴OC＝OD，OA＝OB，
∵在△AOD与△BOC中，
OA=OB∠AOD=∠BOCOD=OC，
∴△AOD≌△BOC（SAS），
∴∠ADO＝∠BCO，∠OAD＝∠OBC，BC＝AD，
∵点H为线段BC的中点，
∴OH＝HB，OH=12BC，
∴∠OBH＝∠HOB＝∠OAD，
又∵∠OAD+∠ADO＝90°，
∴∠ADO+∠BOH＝90°，
∴OH⊥AD，
∵AD＝BC，OH=12BC，
∴OH=12AD．

（2）结论：OH=12AD，OH⊥AD仍成立，
如图2中，延长OH到E，使得HE＝OH，连接BE，

∵点H是BC中点，
∴BH＝CH，
∴△BEH≌△CHO（SAS），
∴OE＝2OH，∠EBC＝∠BCO，
∴∠OBE＝∠EBC+∠OBC＝∠BCO+∠OBC＝180°﹣∠BOC，
∵∠AOB＝∠COD＝90°，
∴∠AOD＝180°﹣∠BOC＝∠OBE，
∵OB＝OA，OC＝OD
∴△BEO≌△ODA（SAS），
∴OE＝AD，∠EOB＝∠DAO，
∴OH=12OE=12AD，
∵∠AOB＝90°，
∴∠DAO+∠AOH＝∠EOB+∠AOH＝90°，
∴OH⊥AD．
24．（2019秋•黄山期末）将两块斜边长相等的等腰直角三角形按如图A摆放，斜边AB分别交CD、CE于M、N点，
（1）如果把图A中的△BCN绕点C逆时针旋转90°得到△ACF，连接FM，如图B，求证：△CMF≌△CMN：
（2）将△CED绕点C旋转：
①当点M、N在AB上（不与A、B重合）时，线段AM、MN、NB之间有一个不变的关系式，请你写出这个关系式，并说明理由；
②当点M在AB上，点N在AB的延长线上（如图C）时，①中的关系式是否仍然成立？请说明理由．

【分析】（1）根据旋转的性质可得CF＝CN，∠ACF＝∠BCN，再求出∠ACM+∠BCN＝45°，从而求出∠MCF＝45°，然后利用“边角边”证明△CMF和△CMN全等即可；
（2）①根据全等三角形对应边相等可得FM＝MN，再根据旋转的性质可得AF＝BN，∠CAF＝∠B＝45°，从而求出∠BAF＝90°，再利用勾股定理列式即可得解；
②把△BCN绕点C逆时针旋转90°得到△ACF，根据旋转的性质可得AF＝BN，CF＝CN，∠BCN＝∠ACF，再求出∠MCF＝∠MCN，然后利用“边角边”证明△CMF和△CMN全等，根据全等三角形对应边相等可得MF＝MN，然后利用勾股定理列式即可得解．
【解析】（1）∵△BCN绕点C逆时针旋转90°得到△ACF，
∴CF＝CN，∠ACF＝∠BCN，
∵∠DCE＝45°，
∴∠ACM+∠BCN＝45°，
∴∠ACM+∠ACF＝45°，
即∠MCF＝45°，
∴∠MCF＝∠MCN，
在△CMF和△CMN中，CF=CN∠MCF=∠MCNCM=CM，
∴△CMF≌△CMN（SAS）；

（2）①∵△CMF≌△CMN，
∴FM＝MN，
又∵∠CAF＝∠B＝45°，
∴∠FAM＝∠CAF+∠BAC＝45°+45°＝90°，
∴AM2+AF2＝FM2，
∴AM2+BN2＝MN2；

②如图，把△BCN绕点C逆时针旋转90°得到△ACF，
则AF＝BN，CF＝CN，∠BCN＝∠ACF，
∵∠MCF＝∠ACB﹣∠MCB﹣∠ACF＝90°﹣（45°﹣∠BCN）﹣∠ACF＝45°+∠BCN﹣∠ACF＝45°，
∴∠MCF＝∠MCN，
在△CMF和△CMN中，CF=CN∠MCF=∠MCNCM=CM，
∴△CMF≌△CMN（SAS），
∴FM＝MN，
∵∠ABC＝45°，
∴∠CAF＝∠CBN＝135°，
又∵∠BAC＝45°，
∴∠FAM＝∠CAF﹣∠BAC＝135°﹣45°＝90°，
∴AM2+AF2＝FM2，
∴AM2+BN2＝MN2．