初中数学人教版八年级下册18.2.1 矩形示范课ppt课件

这是一份初中数学人教版八年级下册18.2.1 矩形示范课ppt课件，共22页。PPT课件主要包含了知识回顾，矩形的定义，探索新知，矩形的性质，请你帮忙，知识源于悟，身边的数学，你说我说等内容，欢迎下载使用。
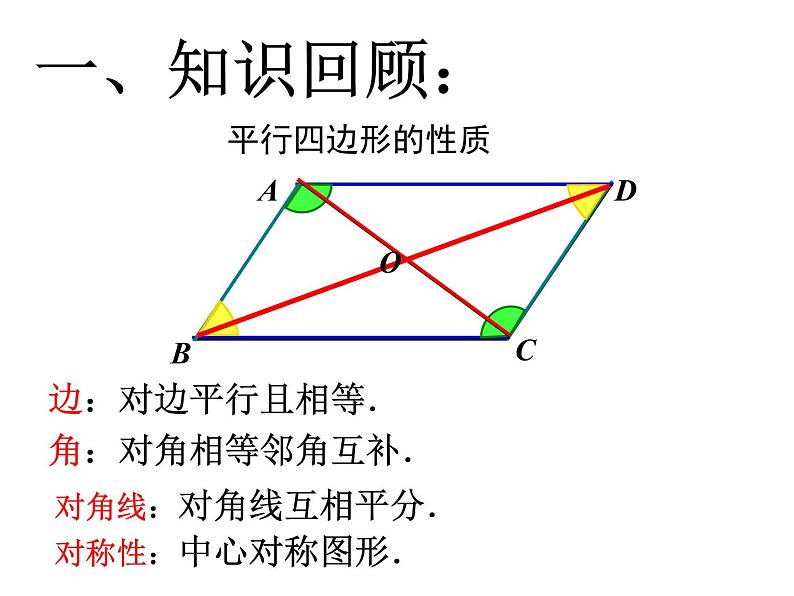
边：对边平行且相等．角：对角相等邻角互补．
对角线：对角线互相平分．
对称性：中心对称图形．
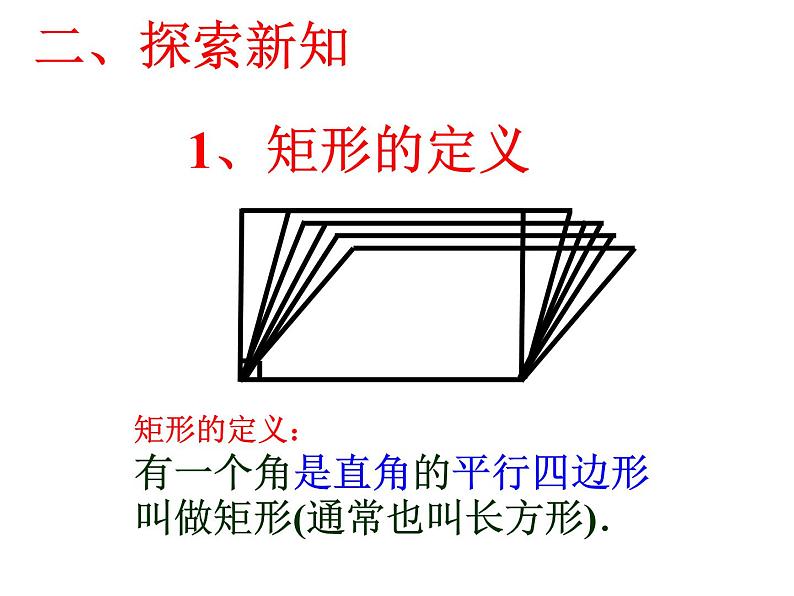
矩形的定义：有一个角是直角的平行四边形叫做矩形(通常也叫长方形)．
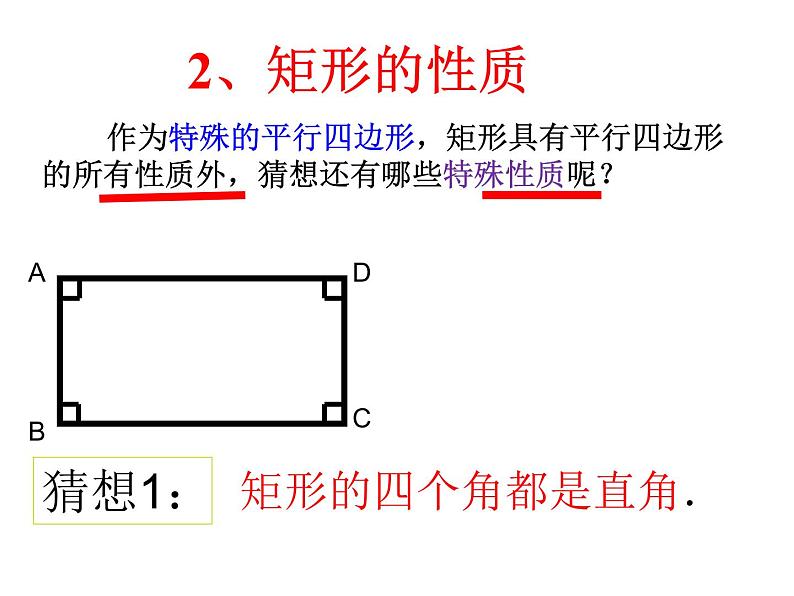
　 作为特殊的平行四边形，矩形具有平行四边形的所有性质外，猜想还有哪些特殊性质呢？
矩形的四个角都是直角．
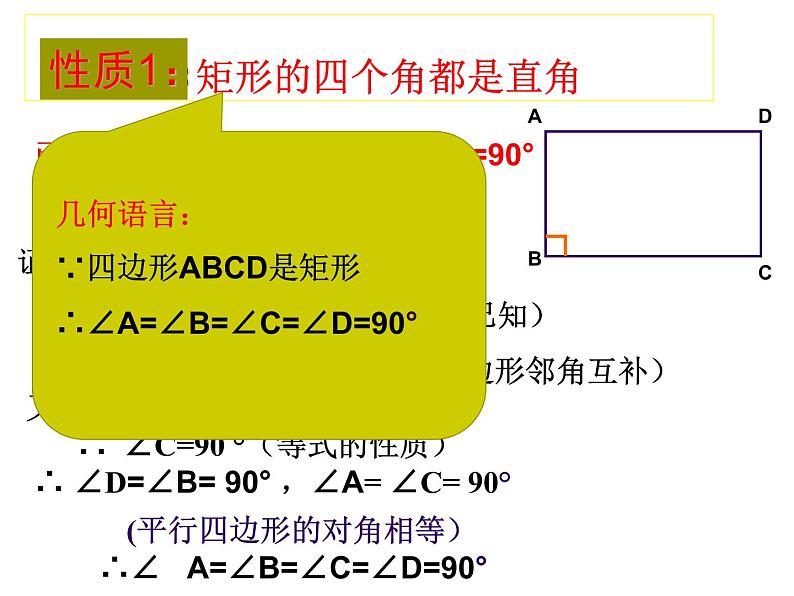
　　 矩形的四个角都是直角
已知：四边形ABCD是矩形, ∠B=90°求证：∠A=∠B=∠C=∠D=90°
证明： ∵矩形ABCD是平行四边形（已知） ∴ ∠B+∠C=180 °（平行四边形邻角互补） 又 ∵ ∠B=90° （已知） ∴ ∠C=90 °（等式的性质） ∴ ∠D=∠B= 90° ，∠A= ∠C= 90°
几何语言：∵四边形ABCD是矩形∴∠A=∠B=∠C=∠D=90°
(平行四边形的对角相等）
∴∠ A=∠B=∠C=∠D=90°
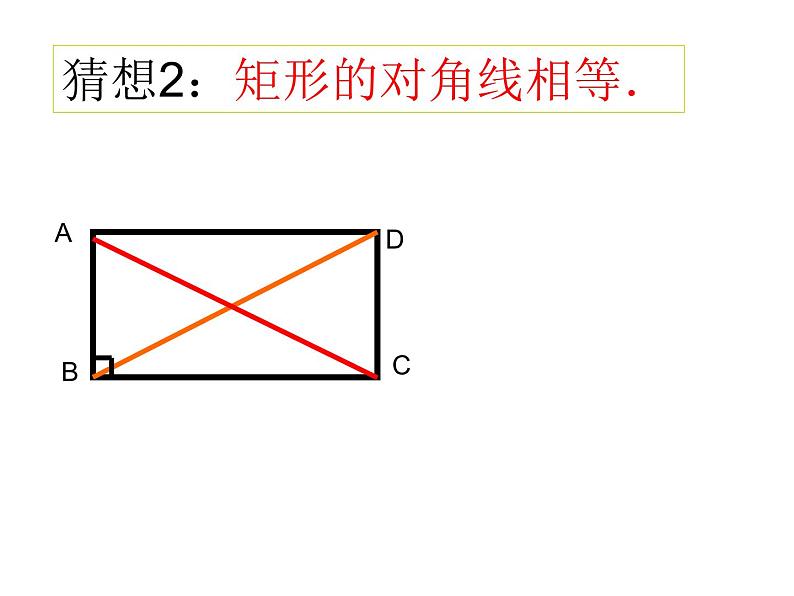
猜想2：矩形的对角线相等．
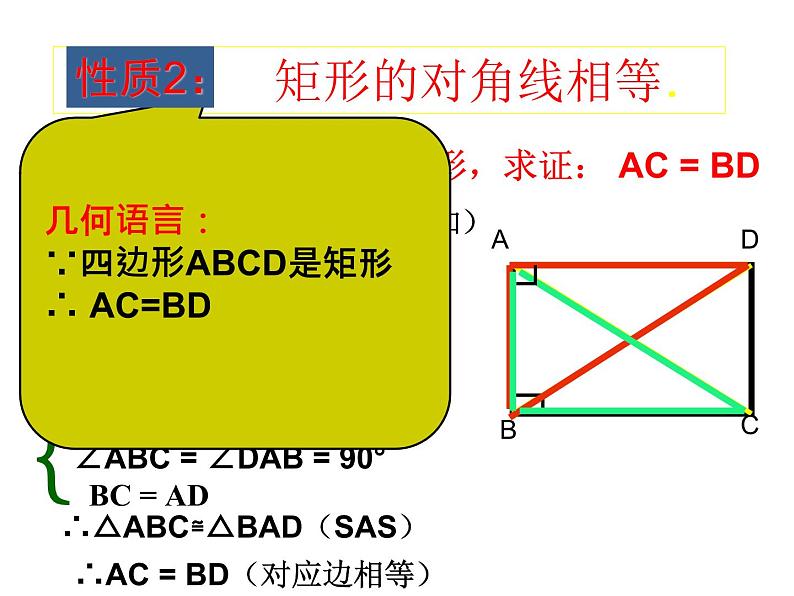
已知：四边形ABCD是矩形，求证： AC = BD
证明： ∵ABCD是矩形（已知）
∴∠ABC = ∠DAB = 90° BC = AD（矩形的性质）
∴△ABC≌△BAD（SAS）
∴AC = BD（对应边相等）
　　 2：矩形的对角线相等．
在△ABC和△BAD中
AB = BA ∠ABC = ∠DAB = 90° BC = AD
几何语言：∵四边形ABCD是矩形∴ AC=BD
例1 如图，矩形ABCD的两条对角线相交于点O，∠AOB=60°，AB=4cm，求矩形对角线的长.
解:∵四边形ABCD是矩形∴AC=BD,AO= AC, BO= BD∴AO=BO∵∠AOB=60°∴△ABO是等边三角形∴AO=AB=BO=4∴AC=BD=2×4=8cm
中心对称图形 轴对称图形
2. 过四边形的各个顶点分别作对角线的平行线，若这四 条平行线围成一个矩形，则原四边形一定是
小明想为本班的进步明星一栏做一个矩形相框。他找来长度相等的两根长木条作为相框的长，找来长度相等两个短木条作为相框的宽，你能帮他检验一下现在的相框是否为矩形吗？
你还有其它方法说明相框是矩形吗？想一想，看看谁的方法多？请大胆猜想，小组交流并加以验证。
在判断相框是否为矩形的过程中能否以下列方法作为依据，为什么？
⑴有一个角是直角的四边形是矩形； ( )
⑵三个角都相等的四边形是矩形 ( )
⑶对角线相等的四边形是矩形； ( )
⑷对角线互相平分且相等的四边形是矩形； ( )
⑸两组对边分别平行，且对角线相等的四边形是矩形。 ( )
给你一根足够长的绳子和一把直角三角尺，你能检验一下教室的黑板面是否为矩形吗？你有几种方法？请说出你的方法和数学依据。
为庆祝“五四”青年运动会，八（10）班的同学要在本班场地布置一个矩形的花坛。计划用串红摆成两条对角线，如果一条对角线用了7盆花，还需搬来多少盆“串红”？如果一条对角线用了6盆呢？你用了什么数学知识?
如图所示的相框，经过测量得AD=BC,AB=DC，另测量数据如图，下面是计算相框面积的过程，你认为步骤完整吗？
解：S矩形ABCD=AB·BC =6×8 =48
说说自己的收获与困惑。
一张四边形纸板ABCD形状如图，它的对角线互相垂直。若要从这张纸板中剪出一个矩形，并且使它的四个顶点分别落在四边形的四条边上，可怎么剪？