北师大版八年级下册2 提公因式法教学课件ppt

学习

目标

1、使学生经历探索寻找多项式各项的公因式的过程，能确定多项式各项的公因式；

2、通过观察、类比等手段，学会用提取公因式法进行因式分解。

重点

掌握用提公因式法把多项式分解因式。

难点

正确地确定多项式的最大公因式。

导入新课

1、什么是因式分解？

2、因式分解与整式乘法有什么关系?

让学生回忆上节课所学习的内容。

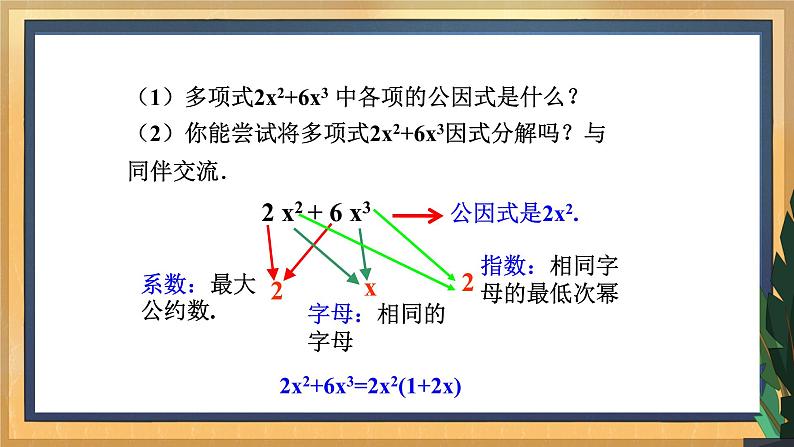
讲授新课

（一）探究提公因式法的定义

1、做一做：

多项式ma+mb+m有共同的因式m，多项式ab+bc各项都含有相同的因式吗？多项式3x2+x呢？多项式mb2+nb-b 呢？尝试将这几个多项式分别写成几个因式的乘积，并与同伴交流．21学生分析讨论，归纳如下：

ab+bc：相同的因式是b； ab+bc=b(a+c)

3x2+x：相同的因式是x；3x2+x=x(3x+1)

mb2+nb-b：相同的因式是b；mb2+nb-b=b(m+n+1)

分析：以上多项式的特点是都有共同的因式

归纳：多项式中各项都含有的相同因式，叫做这个多项式的公因式.

2、议一议：

（1）多项式2x2+6x3 中各项的公因式是什么？

（2）你能尝试将多项式2x2+6x3因式分解吗？与同伴交流．

引导学生分析，找出公因式：

两项都有系数，系数应是2，是2与6的最大公约数.

两项都有含有相同的字母x，x的指数是2与3，应取字母的最低次幂.

所以，多项式2x2+6x3 中各项的公因式是2x2

据此由学生自主完成第二问的问题：

2x2+6x3=2x2(1+2x)

以上进行的因式分解，都是应用的提公因式法，你能总结提公因式法的定义吗？

学生观察分析，归纳总结：

如果一个多项式的各项含有公因式，那么就可以把这个公因式提出来，从而将多项式化成两个因式乘积的形式．这种因式分解的方法叫做提公因式法．

例如：ma+mb+mc=m(a+b+c)

引导学生总结出找公因式的一般步骤：

首先：找各项系数的最大公约数，如2和6的最大公约数是2；

其次：找各项中含有的相同的字母，相同字母的指数取次数最低的．

（二）例题解析

例1、将下列各式分解因式：

（1）3x+6；           （2）7x2-21x；

（3）8a3b2-12ab3c+abc； （4）-24x3-12x2+28x．

分析：首先要找出各项的公因式，然后再提取出来．

学生自主完成，解题过程：

解：（1）3x +x3=x⋅3+x⋅x2 =x(3+x2)；

（2）7x3-21x2=7x2⋅x-7x2⋅3=7x2(x-3)

（3）8a3b2-12ab3c+ab

    =ab⋅8a2b-ab⋅12b2c+ab⋅1

    =ab(8a2b-12b2c+1)；

(4)- 24x3+12x2-28x

 =-(24x3-12x2+28x)

 =-(4x⋅6x2-4x⋅3x+4x⋅7)

=-4x(6x2-3x+7)

根据以上的做题过程。引导学生归纳提公因式法因式分解时的注意事项：

①多项式是几项，提公因式后也剩几项.

②当多项式的某一项和公因式相同时，提公因式后剩余的项是1.

③当多项式第一项的系数是负数时，通常先提出“-”号，使括号内第一项的系数成为正数．在提出“-”号时，多项式的各项都要变号．

4、想一想．

从例1中能否看出提公因式法分解因式与单项式乘以多项式有什么关系？

提公因式法分解因式就是把一个多项式化成单项式与多项式相乘的形式．

例2、把下列各式因式分解：

（1）a（x-3）+2b（x-3）

分析：这个多项式整体而言可分为两大项，即a（x-3）与2b（x-3），每项中都含有（x-3），因此可以把（x-3）作为公因式提出来．

解：a(x-3)+2b(x-3) =(x-3)(a+2b)

（2）y(x+1)+y2(x+1)2．

分析：多项式可看成y(x+1)与+y2(x+1)两项， 相同的部分是y(x+1)， 则公因式为y(x+1)

解：y(x+1)+y2(x+1)2 =y(x+1)[1+y(x+1)]=y(x+1)(xy+y+1 )

例3、把下列各式因式分解：

（1）a(x-y)+b(y-x)

分析：多项式可看成a(x-y)与+b(y-x)两项，其中x-y与y-x互为相反数，  可将+b(y-x)变为-b(x-y)，  则a(x-y)与-b(x-y)的公因式为(x-y)

解：a(x-y)+b(y-x) =a(x-y)-b(x-y) =(x-y)(a-b)

(2)6(m-n)3-12(n-m)2

分析：其中(m-n)与(n-m)互为相反数，可将-12(n-m)2变为-12(m-n)2，  则6(m-n)3与-12(m-n)2公因式为6(m-n)2

解：6(m-n)3-12(n-m)2  =6(m-n)3-12(m-n)2 =6(m-n)2(m-n-2)

注意：①指数为奇数时，交换位置，要添加“-”

②指数为偶数时，只要交换位置即可。

引导学生学会观察，在多项式中寻找相同的因式。

小组讨论，时间3min，总结出正确找出多项式各项公因式的关键。

小组讨论，时间3min，总结出提公因式法的定义。

独立完成，提问学生回答，总结出提公因式法的要点和易错点。

自己总结口诀

独立完成，提问学生回答，注意因式分解的变形。

独立完成，提问学生回答

拓展提高

先分解因式,再求解：已知m+n=8,mn=6,求m2n+mn2的值.

解： m2n+mn2

=mn（m+n）

=6×8

=48

课堂小结

1、公因式的特点

2、提公因式法分解因式的步骤

a.  确定公因式 。

b. “提”公因式（公因式提取要彻底，首项为负先提负，提取公因式莫漏1）。

c.  检验分解因式的结果是否正确。

提问学生自己总结。

作业布置

把下列各式进行因式分解：

（1）3b2+12b           （2）-4m2n-16mn+8m2

（3）18b(a-b)  -12(b-a)