

2021年河南省平顶山市七年级下学期期末数学试卷+答案
展开2020-2021学年河南省平顶山市七年级(下)期末数学试卷
一、选择题(本大题共10个小题,每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的,将正确答案的代号字母用2B铅笔涂在对应的答题卡上
1.下列图形一定是轴对称图形的是( )
A. B. C. D.
2.计算﹣x2•x3的结果为( )
A.﹣x6 B.x6 C.x5 D.﹣x5
3.小明家在火车站的北偏东26°的方向上,那么火车站在小明家的方向为( )
A.北偏东26° B.南偏西26° C.北偏东64° D.南偏西64°
4.PM2.5是指大气中直径小于或等于0.0000025m的细颗粒物,也称为可入肺细颗粒物.它能较长时间悬浮于空气中,其在空气中含量浓度越高,就代表空气污染越严重.若干个直径为0.0000025m的颗粒物首尾连接起来能达到1m,则这些颗粒物的个数为( )
A.2.5×10﹣6 B.2.5×10﹣7 C.400 D.4×105
5.如图,把一个三角形尺ABD的两个顶点B,D分别放置在互相平行的两条直线BC,DE上,其中∠A=45°,∠ADB=90°,如果∠ABC=15°,则∠ADE的度数为( )
A.15° B.20° C.30° D.45°
6.下列事件中是必然事件的为( )
A.400人中至少有两人生日在同一天
B.车辆随机到达一个路口,遇到红灯
C.随机掷一枚均匀的硬币,正面朝上
D.射击运动员小林射靶一次,正中靶心
7.若三角形的两边长分别为6,8,则第三边长可以是( )
A.1 B.2 C.10 D.15
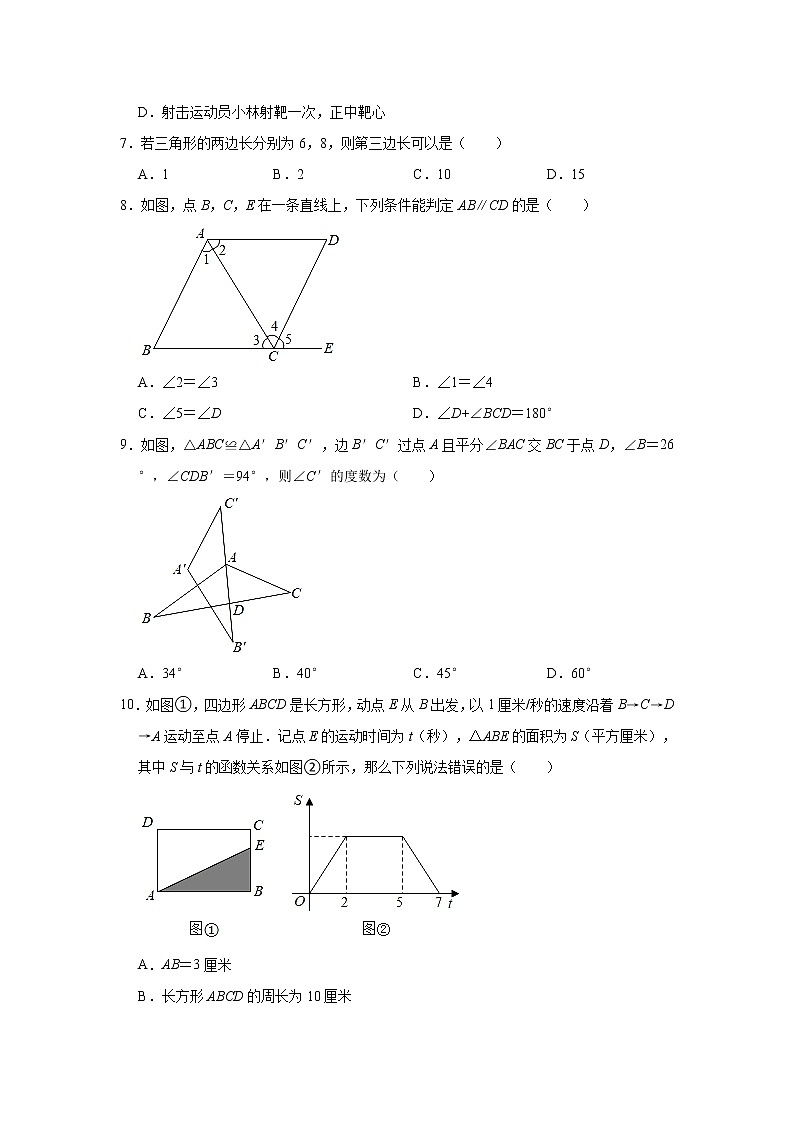
8.如图,点B,C,E在一条直线上,下列条件能判定AB∥CD的是( )
A.∠2=∠3 B.∠1=∠4
C.∠5=∠D D.∠D+∠BCD=180°
9.如图,△ABC≌△A′B′C′,边B′C′过点A且平分∠BAC交BC于点D,∠B=26°,∠CDB′=94°,则∠C′的度数为( )
A.34° B.40° C.45° D.60°
10.如图①,四边形ABCD是长方形,动点E从B出发,以1厘米/秒的速度沿着B→C→D→A运动至点A停止.记点E的运动时间为t(秒),△ABE的面积为S(平方厘米),其中S与t的函数关系如图②所示,那么下列说法错误的是( )
A.AB=3厘米
B.长方形ABCD的周长为10厘米
C.当t=3秒时,S=3平方厘米
D.当S=1.5平方厘米时,t=6秒
二、填空题(本大题共5个小题,每小题3分,共15分)
11.计算:+20210= .
12.如图,已知三地A,B,C在同一条直线上,其中A,B两地之间的距离为100km.一辆汽车从B地出发,以60km/h的速度去C地,则汽车离A地的距离S(km)与汽车行驶的时间t(h)之间的函数关系式为 .
13.如图,在直角三角形ABC中,∠BAC=90°,AB=4,AC=3,BC=5.点P为边BC上一动点,连接AP,则AP的最小值是 .
14.如图,点D在△ABC边AB的延长线上,且AB=BD.以点A为圆心,任意长为半径画弧,分别交△ABC边AC,AB于点M,N;再以点D为圆心,以AN长为半径画弧,交AD于点N′;再以点N′为圆心,以MN长为半径画弧交前弧于点M′,作射线DM′.已知点E为射线DM′上一点,连接BE,请你添加一个条件 ,使△ABC≌△DBE.
15.如图,在△ABC中,AB=AC,BC=5,△ABC的面积为20.DE垂直平分AC,分别交边AB,AC于点D,E,点F为直线DE上一动点,点G为BC的中点,连接FG,FC,则△FGC的周长的最小值为 .
三、解答题(本大题共8个小题,共75分)
16.先化简,再求值:(x+2y)2﹣(2x+y)(2x﹣y)+4x(x﹣y),其中x=﹣2,y=.
17.为加强节约用水,自来水公司对居民用水采用分段计费:每年用水量不超过120立方米时,每立方米水价为a元;当每年用水量超过120立方米但不超过180立方米时,超出部分每立方米水价为b元;当每年用水量超过180立方米时,超出部分每立方米水价为6元.如图是水费y(元)与用水量x(立方米)之间的函数关系图象,结合图象回答下列问题:
(1)a= ,b= ;
(2)若某户居民2020年交水费426元,那么他共用了多少立方米水?
18.某班数学兴趣小组为了测量湛河南北两岸的宽度AB,他们的方法是:让小明从点A出发,沿河岸向东走50步到达电线杆C处,继续前行50步到达D处,然后右转90°直行130步到达E处,这时B,C,E三点在一条直线上.
(1)小组得到结论“DE的长度就是河宽”,请说明其中的道理.
(2)若小明一步的长度为60厘米,请估计河宽有多少米.
19.如图,△ABC和△A'B'C'的顶点都在边长为1的正方形网格的格点上,且△ABC和△A'B'C'关于直线m成轴对称.
(1)直接写出△ABC的面积 ;
(2)请在如图所示的网格中作出对称轴m.
(3)请在线段BC的上方找一点D,画出△DCB,使△ABC≌△DCB.
20.如图,已知△ABC,AD平分∠BAC交BC于点D,AE⊥BC于点E,∠B<∠C.
(1)若∠B=44°,∠C=72°,求∠DAE的度数;
(2)若∠B=27°,当∠DAE= 度时,∠ADC=∠C.
21.某儿童用品商店在“六一”儿童节设置了一个购物摸球游戏:在一不透明的箱子里装了50个小球,这些球分别标有50元,8元,2元,0元的金额,其中标有50元的小球有4个,标有0元小球有5个,标有2元小球的个数比标有8元小球的个数的2倍少1,这些小球除数字外都相同,并规定:凡购买指定商品,可以摸球一次,如果摸到标有50元,8元,2元的小球,则可以得到等价值的奖品一个.
已知小明购买了指定商品,根据以上信息回答下列问题:
(1)小明获得奖品的概率是 ,获得8元奖品的概率是 .
(2)为吸引顾客,儿童用品店现将8元奖品的获奖概率提高到,在保持小球总数不变的情况下,需要把几个标有2元的小球改为8元的小球.
22.我们将(a+b)2=a2+2ab+b2进行变形,如:a2+b2=(a+b)2﹣2ab,ab=等.根据以上变形解决下列问题:
(1)已知a2+b2=8,(a+b)2=48,则ab= .
(2)已知,若x满足(25﹣x)(x﹣10)=﹣15,求(25﹣x)2+(x﹣10)2的值.
(3)如图,四边形ABED是梯形,DA⊥AB,EB⊥AB,AD=AC,BE=BC,连接CD,CE,若AC•BC=10,则图中阴影部分的面积为 .
23.如图,已知C为直线a上一点,过点C作射线CD⊥a,在射线CD上取一点A,以AC为斜边作等腰直角△ABC,其中∠ABC=90°,AB=BC,AC=10.若M,N两点同时从点C出发,其中点M沿C→D方向以每秒3个单位长度在射线CD上运动,点N在直线a上同时以每秒2个单位长度向上或向下运动,连接BM,BN,设运动时间为t(秒).
(1)根据题意用含t的代数式表示MC= ,NC= .
(2)当点N向上运动,且点M运动到AC中点时,求CN的长;
(3)当t等于多少时,△ABM与△BCN全等,说明理由.
参考答案
一、选择题(本大题共10个小题,每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的,将正确答案的代号字母用2B铅笔涂在对应的答题卡上
1.下列图形一定是轴对称图形的是( )
A. B. C. D.
【分析】根据轴对称图形的概念判断即可.如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
解:A.是轴对称图形,故本选项符合题意;
B.不是轴对称图形,故本选项不合题意;
C.不是轴对称图形,故本选项不合题意;
D.不是轴对称图形,故本选项不合题意.
故选:A.
2.计算﹣x2•x3的结果为( )
A.﹣x6 B.x6 C.x5 D.﹣x5
【分析】直接用同底数幂的乘法法则计算.
解:﹣x2•x3
=﹣(x2•x3)
=﹣x2+3
=﹣x5.
故选:D.
3.小明家在火车站的北偏东26°的方向上,那么火车站在小明家的方向为( )
A.北偏东26° B.南偏西26° C.北偏东64° D.南偏西64°
【分析】根据位置的相对性可知,它们的方向相反,角度相等,距离相等,据此解答.
解:小明家在火车站的北偏东26°的方向上,那么火车站在小明家的方向为:南偏西26°.
故选:B.
4.PM2.5是指大气中直径小于或等于0.0000025m的细颗粒物,也称为可入肺细颗粒物.它能较长时间悬浮于空气中,其在空气中含量浓度越高,就代表空气污染越严重.若干个直径为0.0000025m的颗粒物首尾连接起来能达到1m,则这些颗粒物的个数为( )
A.2.5×10﹣6 B.2.5×10﹣7 C.400 D.4×105
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是非负数;当原数的绝对值<1时,n是负数.
解:1÷0.0000025=4×105(个),
故选:D.
5.如图,把一个三角形尺ABD的两个顶点B,D分别放置在互相平行的两条直线BC,DE上,其中∠A=45°,∠ADB=90°,如果∠ABC=15°,则∠ADE的度数为( )
A.15° B.20° C.30° D.45°
【分析】由∠A=45°,∠ADB=90°可得∠ABD=45°,则∠CBD=60°,利用平行线的性质可得∠1=∠CBD=60°,则∠ADE=180°﹣∠ADB﹣∠1,代入相应数值求解即可.
解:如图所示:
∵∠A=45°,∠ADB=90°,
∴∠ABD=45°,
∵∠ABC=15°,
∴∠CBD=∠ABC+∠ABD=60°,
∵BC∥DE,
∴∠1=∠CBD=60°,
∴∠ADE=180°﹣∠ADB﹣∠1=30°.
故选:C.
6.下列事件中是必然事件的为( )
A.400人中至少有两人生日在同一天
B.车辆随机到达一个路口,遇到红灯
C.随机掷一枚均匀的硬币,正面朝上
D.射击运动员小林射靶一次,正中靶心
【分析】必然事件就是一定发生的事件,即发生的概率是1的事件.
解:A、400人中至少有两人生日在同一天是必然事件,符合题意;
B、车辆随机到达一个路口,可能遇到红灯,有可能遇到的不是红灯,因此是随机事件,不符合题意;
C、掷一枚质地均匀的硬币,可能正面向上,有可能反面朝上,因此是随机事件,不符合题意;
D、某射击运动员射靶一次,可能正中靶心,也可能不中靶心,是随机事件,不符合题意.
故选:A.
7.若三角形的两边长分别为6,8,则第三边长可以是( )
A.1 B.2 C.10 D.15
【分析】已知两边,则第三边的长度应是大于两边的差而小于两边的和,这样就可求出第三边长的范围.
解:设第三边的长为x,根据三角形的三边关系,
得8﹣6<x<8+6,
即2<x<14,
只有10适合,
故选:C.
8.如图,点B,C,E在一条直线上,下列条件能判定AB∥CD的是( )
A.∠2=∠3 B.∠1=∠4
C.∠5=∠D D.∠D+∠BCD=180°
【分析】根据平行线的判定逐一进行判断即可.
解:A.因为∠2=∠3,
所以AD∥BC,故A选项不符合题意;
B.因为∠1=∠4,
所以AB∥DC,故B选项符合题意;
C.因为∠5=∠D,
所以AD∥BC,故C选项不符合题意;
D.因为∠D+∠BCD=180°,
所以AD∥BC,故A选项不符合题意;
故选:B.
9.如图,△ABC≌△A′B′C′,边B′C′过点A且平分∠BAC交BC于点D,∠B=26°,∠CDB′=94°,则∠C′的度数为( )
A.34° B.40° C.45° D.60°
【分析】根据对顶角相等求出∠ADB,根据三角形内角定理求出∠BAD,根据角平分线的定义求出∠BAC,进而求出∠C,根据全等三角形对应角相等解答即可.
解:∵∠CDB′=94°,
∴∠ADB=∠CDB′=94°,
∴∠BAD=180°﹣∠B﹣∠ADB=60°,
∵AB′平分∠BAC,
∴∠BAC=2∠BAD=120°,
∴∠C=180°﹣∠B﹣∠BAC=34°,
∵△ABC≌△A′B′C′,
∴∠C′=∠C=34°,
故选:A.
10.如图①,四边形ABCD是长方形,动点E从B出发,以1厘米/秒的速度沿着B→C→D→A运动至点A停止.记点E的运动时间为t(秒),△ABE的面积为S(平方厘米),其中S与t的函数关系如图②所示,那么下列说法错误的是( )
A.AB=3厘米
B.长方形ABCD的周长为10厘米
C.当t=3秒时,S=3平方厘米
D.当S=1.5平方厘米时,t=6秒
【分析】通过图②发现:t=2、5、7时,△ABE的面积为S的变化趋势发生变化得到长方形的长和宽,从而判断出A、B选项正确;t=3秒时点E在DA上运动根据三角形面积公式可判断C正确;S=1.5平方厘米时,点E可能在BC上,也可能在DA上,求出此时的t值即可.
解:∵0≤t≤2时,△ABE的面积S越来越大,
∴0≤t≤2时,动点E在BC上运动,
∴BC=2×1=2(厘米).
∵2≤t≤5时,△ABE的面积S不变,
∴0≤t≤2时,动点E在CD上运动,
∴CD=AB=(5﹣2)×1=3(厘米).
∴A选项正确,不符合题意.
长方形ABCD的周长=(3+2)×2=10(厘米),
∴B选项正确,不符合题意.
∵2<3<5,
∴当t=3秒时,动点E在CD上运动,S=3×2÷2=3(平方厘米),
∴B选项正确,不符合题意.
∵S=1.5<3,
∴S=1.5平方厘米时,点E在BC或DA上,
当点E在DA上时,
t×3×=1.5,
解得:t=1,
当点E在DA上时,
(t﹣3﹣2)×=1.5,
解得:t=6,
∴S=1.5平方厘米时,t=6或1.
∴D选项错误,符合题意.
故选:D.
二、填空题(本大题共5个小题,每小题3分,共15分)
11.计算:+20210= 26 .
【分析】直接利用负整数指数幂的性质以及零指数幂的性质分别化简得出答案.
解:原式=25+1
=26.
故答案为:26.
12.如图,已知三地A,B,C在同一条直线上,其中A,B两地之间的距离为100km.一辆汽车从B地出发,以60km/h的速度去C地,则汽车离A地的距离S(km)与汽车行驶的时间t(h)之间的函数关系式为 S=60t+100 .
【分析】如图,汽车出发时离A地的距离是100km,又走了60tkm,所以汽车离A地的距离S=60t+100.
解:如图,
∵一辆汽车从B地出发,以60km/h的速度去C地,
∴汽车的路程=60t(km),
∴汽车离A地的距离S=60t+100.
故答案为:S=60t+100.
13.如图,在直角三角形ABC中,∠BAC=90°,AB=4,AC=3,BC=5.点P为边BC上一动点,连接AP,则AP的最小值是 .
【分析】依据垂线段最短,即可得到当AP⊥BC时,AP最短.根据面积法求得垂线段AP的长即可.
解:如图所示,当AP⊥BC时,AP最短,
∵=,
∴AP===,
∴AP的最小值是.
故答案为:.
14.如图,点D在△ABC边AB的延长线上,且AB=BD.以点A为圆心,任意长为半径画弧,分别交△ABC边AC,AB于点M,N;再以点D为圆心,以AN长为半径画弧,交AD于点N′;再以点N′为圆心,以MN长为半径画弧交前弧于点M′,作射线DM′.已知点E为射线DM′上一点,连接BE,请你添加一个条件 AC=DE或∠C=∠E或∠ABC=∠DBE, ,使△ABC≌△DBE.
【分析】根据全等三角形的判定方法解决问题即可.
解:由作图可知,∠A=∠D,AB=AC,
故添加:AC=DE或∠C=∠E或∠ABC=∠DBE,可以使得△ABC≌△DBE.
故答案为:AC=DE或∠C=∠E或∠ABC=∠DBE,
15.如图,在△ABC中,AB=AC,BC=5,△ABC的面积为20.DE垂直平分AC,分别交边AB,AC于点D,E,点F为直线DE上一动点,点G为BC的中点,连接FG,FC,则△FGC的周长的最小值为 .
【分析】由DE是AC的垂直平分线,可知A与C关于DE对称,连接AG,CF,此时FC+FG最短,再由已知求出AG=8,则△FGC的周长AG+CG=,即为所求.
解:∵DE是AC的垂直平分线,
∴A与C关于DE对称,
连接AG,CF,
∴GF+FC=AF+FG=AG,此时FC+FG最短,
∵AB=AC,点G为BC的中点,
∴AG⊥BC,
∵BC=5,△ABC的面积为20,
∴AG=8,
∴△FGC的周长=FC+FG+GC=AG+CG=8+=,
∴△FGC的周长的最小值为,
故答案为.
三、解答题(本大题共8个小题,共75分)
16.先化简,再求值:(x+2y)2﹣(2x+y)(2x﹣y)+4x(x﹣y),其中x=﹣2,y=.
【分析】根据整式的加减运算法则以及乘除运算法则进行化简,然后将x与y的值代入原式即可求出答案.
解:原式=x2+4xy+4y2﹣(4x2﹣y2)+4x2﹣4xy
=x2+4xy+4y2﹣4x2+y2+4x2﹣4xy
=x2+5y2,
当x=﹣2,y=时,
原式=4+5×
=.
17.为加强节约用水,自来水公司对居民用水采用分段计费:每年用水量不超过120立方米时,每立方米水价为a元;当每年用水量超过120立方米但不超过180立方米时,超出部分每立方米水价为b元;当每年用水量超过180立方米时,超出部分每立方米水价为6元.如图是水费y(元)与用水量x(立方米)之间的函数关系图象,结合图象回答下列问题:
(1)a= 2 ,b= 3 ;
(2)若某户居民2020年交水费426元,那么他共用了多少立方米水?
【分析】(1)根据图象即可求得;
(2)当用户用180立方米水时,水费为420元,可判断水费为426元时,用水量超过180立方米,根据每部分的水费算出用水量即可.
解:(1)根据图象当用水量为120时,总费用为240元,每年用水量不超过120立方米时,每立方米水价a=240÷120=2(元),
根据图象当用水量为140时,总费用为300元,每年用水量超过120立方米但不超过180立方米时,超出部分每立方米水价为b=(300﹣240)÷(140﹣120)=3(元),
故答案为:2,3;
(2)由题意可知,用水量为180立方米时,水费为,
240+(180﹣120)×3=420元,
而426>420,所以用水量炒股180立方米,
∴(426﹣420)÷6=1,
即水费为426时,用水量为180+1=181立方米.
18.某班数学兴趣小组为了测量湛河南北两岸的宽度AB,他们的方法是:让小明从点A出发,沿河岸向东走50步到达电线杆C处,继续前行50步到达D处,然后右转90°直行130步到达E处,这时B,C,E三点在一条直线上.
(1)小组得到结论“DE的长度就是河宽”,请说明其中的道理.
(2)若小明一步的长度为60厘米,请估计河宽有多少米.
【分析】根据AB⊥AD,ED⊥AD可知∠BAC=∠EDC,再由AC=DC,∠ACB=∠ECD可得出△ABC≌△EDC,由全等三角形的性质即可得出结论.
解:(1)∵AB⊥AD,ED⊥AD,
∴∠BAC=∠EDC,
在△ABC与△DEC中,
,
∴△ABC≌△DEC(ASA),
∴DE=AB;
(2)∵DE=130×0.6=78(米),
∴河宽AB=78米.
19.如图,△ABC和△A'B'C'的顶点都在边长为1的正方形网格的格点上,且△ABC和△A'B'C'关于直线m成轴对称.
(1)直接写出△ABC的面积 5 ;
(2)请在如图所示的网格中作出对称轴m.
(3)请在线段BC的上方找一点D,画出△DCB,使△ABC≌△DCB.
【分析】(1)用一个矩形的面积分别减去三个直角三角形的面积去计算△ABC的面积;
(2)利用网格特点作BB′、CC′的垂直平分线得到对称轴m;
(3)平移AB使B点与C点重合,则A点的对应点为D点.
解:(1)△ABC的面积=4×4﹣×1×2﹣×2×4﹣×3×4=5;
故答案为5;
(2)如图,直线m为所作;
(3)如图,△DCB为所作.
20.如图,已知△ABC,AD平分∠BAC交BC于点D,AE⊥BC于点E,∠B<∠C.
(1)若∠B=44°,∠C=72°,求∠DAE的度数;
(2)若∠B=27°,当∠DAE= 21 度时,∠ADC=∠C.
【分析】(1)利用三角形的内角和求出∠BAC,再利用内角与外角的关系先求出∠ADC,再求出∠DAE;
(2)利用三角形的内角和定理及推论,用含∠C的代数式表示出∠BAC、∠ADC,根据∠C=∠ADC得到关于∠C的方程,先求出∠C,再求出∠DAE的度数.
解:∵AD平分∠BAC交BC于点D,AE⊥BC于点E,
∴∠BAD=∠CAD=∠BAC,∠AED=90°.
(1)∵∠B=44°,∠C=72°,
∴∠BAC=180°﹣∠B﹣∠C
=180°﹣44°﹣72°
=64°.
∴∠BAD=×64°=32°.
∵∠ADC=∠B+∠BAD
=44°+32°
=76°,
∴∠DAE=90°﹣∠ADC
=90°﹣76°
=14°.
(2)∵∠B=27°,∠C=∠ADC,
∴∠BAC=180°﹣∠B﹣∠C
=180°﹣27°﹣∠C
=153°﹣∠C.
∴∠BAD=×(153°﹣∠C)
=76.5°﹣.
∴∠ADC=∠B+∠BAD
=27°+76.5°﹣∠C
=103.5°﹣∠C.
∵∠ADC=∠C,
∴103.5°﹣∠C=∠C.
∴∠ADC=∠C=69°.
∴∠DAE=∠AED﹣∠ADC
=90°﹣69°
=21°.
故答案为:21.
21.某儿童用品商店在“六一”儿童节设置了一个购物摸球游戏:在一不透明的箱子里装了50个小球,这些球分别标有50元,8元,2元,0元的金额,其中标有50元的小球有4个,标有0元小球有5个,标有2元小球的个数比标有8元小球的个数的2倍少1,这些小球除数字外都相同,并规定:凡购买指定商品,可以摸球一次,如果摸到标有50元,8元,2元的小球,则可以得到等价值的奖品一个.
已知小明购买了指定商品,根据以上信息回答下列问题:
(1)小明获得奖品的概率是 ,获得8元奖品的概率是 .
(2)为吸引顾客,儿童用品店现将8元奖品的获奖概率提高到,在保持小球总数不变的情况下,需要把几个标有2元的小球改为8元的小球.
【分析】(1)求出标有“8元”“2元”的小球个数,即可求出“获奖”的概率,获得“8元的概率;
(2)根据“8元”的概率为,列方程求解.
解:(1)设标有“8元”的小球有x个,则标有“2元”的小球有(2x﹣1)个,
由题意得,
x+2x﹣1+4+5=50,
解得x=14,
2x﹣1=27,
即标有“8元”的小球有14个,则标有“2元”的小球有27个,
所以“获奖”的概率为=,
共有50个小球,标有“8元”的有14个,
因此获得“8元”的概率为=,
故答案为:,;
(2)设需要y个标有“2元”的小球改为“8元”,由题意得,
=,
解得y=6,
因为原来有27个标有“2元”的小球,
所以需要将6个标有“2元”的小球改为标为“8元”的小球.
22.我们将(a+b)2=a2+2ab+b2进行变形,如:a2+b2=(a+b)2﹣2ab,ab=等.根据以上变形解决下列问题:
(1)已知a2+b2=8,(a+b)2=48,则ab= 20 .
(2)已知,若x满足(25﹣x)(x﹣10)=﹣15,求(25﹣x)2+(x﹣10)2的值.
(3)如图,四边形ABED是梯形,DA⊥AB,EB⊥AB,AD=AC,BE=BC,连接CD,CE,若AC•BC=10,则图中阴影部分的面积为 10 .
【分析】(1)将a2+b2=8,(a+b)2=48代入题干中的推导公式就可求得结果;
(2)设25﹣x=a,x﹣10=b,则(25﹣x)2+(x﹣10)2=a2+b2=(a+b)2﹣2ab,再代入计算即可;
(3)设AD=AC=a,BE=BC=b,则图中阴影部分的面积为(a+b)(a+b)﹣a²﹣b²=[(a+b)²﹣(a²+b²)]=×2ab=ab=10.
【解答】(1)∵a2+b2=8,(a+b)2=48,
∴ab===20,
(2)设25﹣x=a,x﹣10=b,
由(a+b)2=a2+2ab+b2进行变形得,
a2+b2=(a+b)2﹣2ab,
∴(25﹣x)2+(x﹣10)2
=[(25﹣x)+(x﹣10)]²﹣2(25﹣x)(x﹣10)
=15²﹣2×(﹣15)
=225+30
=255,
(3)设AD=AC=a,BE=BC=b,
则图中阴影部分的面积为(a+b)(a+b)﹣(a²+b²)
=[(a+b)²﹣(a²+b²)]
=×2ab
=ab
=10
23.如图,已知C为直线a上一点,过点C作射线CD⊥a,在射线CD上取一点A,以AC为斜边作等腰直角△ABC,其中∠ABC=90°,AB=BC,AC=10.若M,N两点同时从点C出发,其中点M沿C→D方向以每秒3个单位长度在射线CD上运动,点N在直线a上同时以每秒2个单位长度向上或向下运动,连接BM,BN,设运动时间为t(秒).
(1)根据题意用含t的代数式表示MC= 3t ,NC= 2t .
(2)当点N向上运动,且点M运动到AC中点时,求CN的长;
(3)当t等于多少时,△ABM与△BCN全等,说明理由.
【分析】(1)根据路程等于时间乘以速度得出MC,NC即可;
(2)根据点M运动到CA中点时,得出关于t的方程解答即可;
(3)分当点N向上运动时和当点N向下运动时,两种情况,利用全等三角形的性质得出方程解答即可.
解:(1)根据题意可得:MC=3t,NC=2t,
故答案为:3t;2t;
(2)当点M运动到CA中点时,CM=5,
∴t=,
∴CN=;
(3)如图1,
当点N向上运动时,
∵AB=BC,∠ABC=90°,
∴∠BAM=∠BCA=45°,
∵a⊥CD,
∴∠BCN=∠BAM=45°,
要使△ABM与△BCN全等,需要AM=CN,
∴10﹣3t=2t,
∴t=2,
当t=2时,△ABM≌△BCN,
如图2,
当点N向下运动时,
MA=3t﹣10,CN=2t,
∵∠MAB=∠NCB=180°﹣45°=135°,BA=BC,
当AM=CN时,△ABM≌△CBN,
∴3t﹣10=2t,
∴t=10,
综上所述,t=2或10时,△ABM与△BCN全等.
2023-2024学年河南省平顶山市宝丰县七年级(下)期末数学试卷(含答案): 这是一份2023-2024学年河南省平顶山市宝丰县七年级(下)期末数学试卷(含答案),共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年河南省平顶山市叶县七年级(下)期末数学试卷(含答案解析): 这是一份2022-2023学年河南省平顶山市叶县七年级(下)期末数学试卷(含答案解析),共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
河南省平顶山市汝州市2021-2022学年七年级下学期期末数学试卷(word版含答案): 这是一份河南省平顶山市汝州市2021-2022学年七年级下学期期末数学试卷(word版含答案),共28页。试卷主要包含了选择题,填空题,解答等内容,欢迎下载使用。












