
2021-2022学年四川省眉山市丹棱县七年级(上)期末数学试卷 解析版
展开1.(4分)2的相反数是( )
A.2B.﹣2C.D.±2
2.(4分)气温由﹣5℃上升了4℃时的气温是( )
A.﹣1℃B.1℃C.﹣9℃D.9℃
3.(4分)如图所示的主视图对应的几何体是( )
A.B.C.D.
4.(4分)2021年2月25日,习近平总书记庄严宣告,我国脱贫攻坚战取得全面胜利.现标准下,98990000农村贫困人口全部脱贫.数98990000用科学记数法表示为( )
A.98.99×106B.9.899×107C.9899×104D.0.9899×108
5.(4分)下列计算正确的是( )
A.a+a=a2B.6a3﹣5a2=a
C.3a2+2a3=5a5D.3a2b﹣4ba2=﹣a2b
6.(4分)点C是线段AB的中点,点D是线段AC的三等分点.若线段AB=12cm,则线段BD的长为( )
A.10cmB.8cmC.10cm或8cmD.2cm或4cm
7.(4分)如图,已知直线a∥b,∠1=50°,则∠2的度数为( )
A.140°B.130°C.50°D.40°
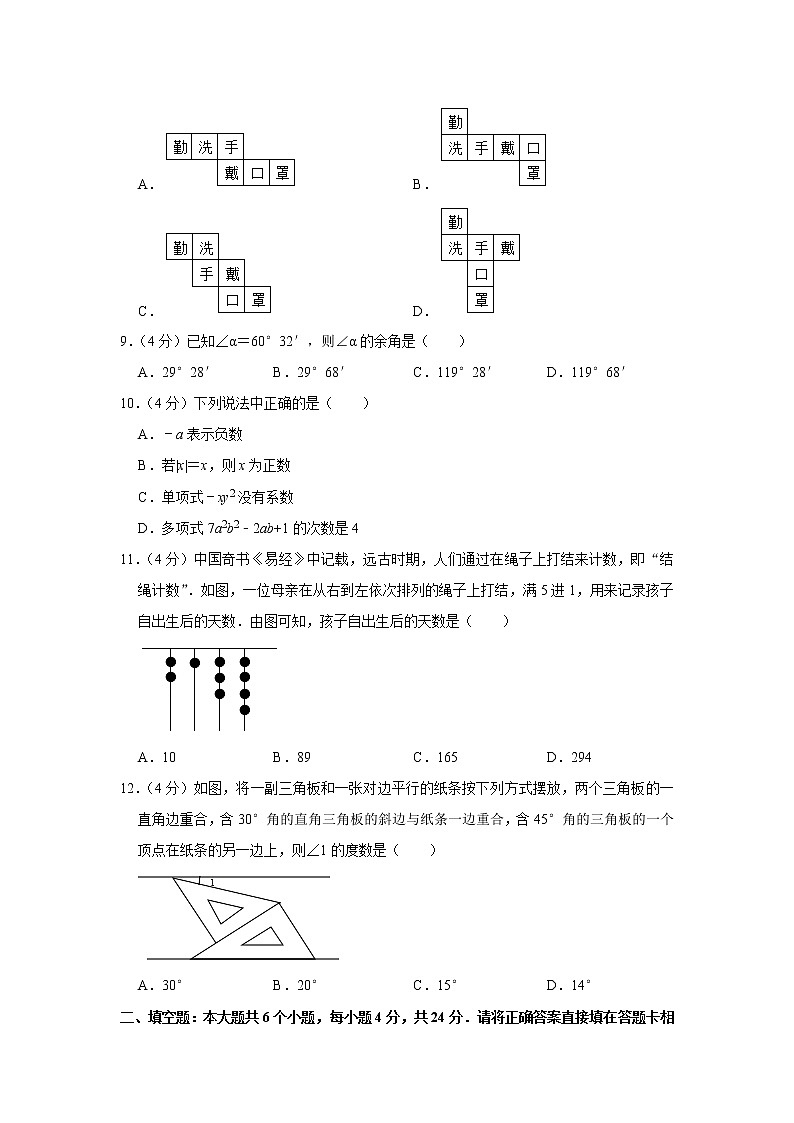
8.(4分)下列正方体的展开图上每个面上都有一个汉字.其中,手的对面是口的是( )
A.B.
C.D.
9.(4分)已知∠α=60°32′,则∠α的余角是( )
A.29°28′B.29°68′C.119°28′D.119°68′
10.(4分)下列说法中正确的是( )
A.﹣a表示负数
B.若|x|=x,则x为正数
C.单项式﹣xy2没有系数
D.多项式7a2b2﹣2ab+1的次数是4
11.(4分)中国奇书《易经》中记载,远古时期,人们通过在绳子上打结来计数,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满5进1,用来记录孩子自出生后的天数.由图可知,孩子自出生后的天数是( )
A.10B.89C.165D.294
12.(4分)如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
A.30°B.20°C.15°D.14°
二、填空题:本大题共6个小题,每小题4分,共24分.请将正确答案直接填在答题卡相应的位置上.
13.(4分)用“>”或“<”符号填空:﹣7 ﹣9.
14.(4分)若2a3bm与3anb2是同类项,则(m﹣n)2= .
15.(4分)已知a﹣b=3,c+d=2,则(b+c)﹣(a﹣d)的值为 .
16.(4分)如图,小张从家(图中A处)出发,向南偏东40°的方向走到学校(图中B处)再从学校出发,向北偏西75°的方向走到小明家(图中C处),则∠ABC为 度.
17.(4分)图1是一个正方体的展开图,该正方体从图2所示的位置依次翻到第1格,第2格,第3格,此时小正方体朝上一面的字是 .
18.(4分)我们规定这样一种运算:如果ab=N(a>0,N>0),那么b就叫做以a为底的N的对数,记做b=lgaN.例如:因为23=8,所以lg28=3,那么lg381的值为 .
三、解答题:本大题共8个小题,共78分.
19.(8分)计算:
(1)﹣14+5﹣(﹣10)+8
(2)﹣22+(﹣)3÷(﹣2)×8
20.(12分)(1)先化简,再求值:4x2﹣(2x2+x﹣1)+(2﹣2x2﹣3x),其中x=﹣.
(2)如图,∠AOB=60°,∠AOC=90°,OC是∠BOD的平分线,求∠COD的度数.
21.(8分)如图,已知直线l和直线外A,B,C三点,按下列要求并作答.
(1)画射线AB;
(2)连接BC;
(3)延长CB至点D,使得BD=BC;
(4)在直线l上确定一点E,使得AE最小,请写出你作图的依据.
22.(8分)为了提高足球球员快速抢断转身能力,教练设计了折返跑训练.在足球场上画一条东西方向的直线,如果约定向东为正,向西为负,一组折返跑训练的记录如下(单位:米):40,﹣30,+50,﹣25,+25,﹣30,+15,﹣28,+16,﹣18.
(1)球员最后到达的地方在出发点的哪个方向?距出发点多远?
(2)在这组训练过程中,球员最远处离出发点多远?
(3)球员在这组训练过程中,共跑了多少米?
23.(10分)阅读下列推理过程,在括号中填写理由.
如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°.
试说明:∠GDC=∠B.
解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90° ( )
∴EF∥AD ( )
∴ +∠2=180° ( )
又∵∠2+∠3=180°(已知)
∴∠1= ( )
∴ ∥ ( )
∴∠GDC=∠B ( )
24.(10分)如图,若干个完全相同的小正方体堆成一个几何体.
(1)请在方格中画出该几何体的左视图和俯视图.
(2)用小立方体搭一个几何体,使得它的左视图和俯视图与你在方格中所画的一致,则这样的几何体最少要 个小立方块,最多要 个小立方块.
(3)若小正方体的棱长为2cm,请求出图1中几何体的表面积.
25.(10分)根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从2017年5月1日起对居民生活用电实施“阶梯电价”收费,具体收费标准见下表:
实施“阶梯电价”收费以后,该市居民陈先生家积极响应号召节约用电,2019年10月用电100千瓦时,交电费50元.
(1)求上表中a的值.
(2)陈先生家2019年11月用电200千瓦时,应交费多少元?
(3)若陈先生家2019年12月份的用电量为x千瓦时(x>150),请用含x的代数式表示陈先生一家应交多少元电费.
26.(12分)如图,已知点C在线段AB上,线段AC=12厘米,BC=8厘米,点M,N分别是AC,BC的中点.
(1)求线段MN的长;
(2)根据第(1)题的计算过程和结果,设AC+BC=a,其它条件不变,直接写出MN的长度;
(3)动点P、Q分别从A,B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿BA向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动,设运动时间为x秒,是否存在某一时刻,使得C、P、Q这三个点中,有一个点恰为另外两点所连线段的中点?若存在,求出所有满足条件的x的值;若不存在,请说明理由.
2021-2022学年四川省眉山市丹棱县七年级(上)期末数学试卷
参考答案与试题解析
一、选择题:本大题共12个小题,每小题4分,共48分.在每个小题给出的四个选项中,只有一项是正确的,请在答题卡上把相应题目的正确选项涂黑.
1.(4分)2的相反数是( )
A.2B.﹣2C.D.±2
【分析】直接利用相反数的定义得出答案.
【解答】解:2的相反数是:﹣2.
故选:B.
2.(4分)气温由﹣5℃上升了4℃时的气温是( )
A.﹣1℃B.1℃C.﹣9℃D.9℃
【分析】根据题意列出算式,计算即可求出值.
【解答】解:根据题意得:﹣5+4=﹣1,
则气温由﹣5℃上升了4℃时的气温是﹣1℃.
故选:A.
3.(4分)如图所示的主视图对应的几何体是( )
A.B.C.D.
【分析】根据主视图是在正面内得到的由前向后观察物体的视图,逐一判断即可.
【解答】解:A、主视图为,故此选项不合题意;
B、主视图为,故此选项符合题意;
C、主视图为,故此选项不合题意;
D、主视图为,故此选项不合题意.
故选:B.
4.(4分)2021年2月25日,习近平总书记庄严宣告,我国脱贫攻坚战取得全面胜利.现标准下,98990000农村贫困人口全部脱贫.数98990000用科学记数法表示为( )
A.98.99×106B.9.899×107C.9899×104D.0.9899×108
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于或等于10时,n是正整数;当原数的绝对值小于1时,n是负整数.
【解答】解:98990000=9.899×107,
故选:B.
5.(4分)下列计算正确的是( )
A.a+a=a2B.6a3﹣5a2=a
C.3a2+2a3=5a5D.3a2b﹣4ba2=﹣a2b
【分析】根据合并同类项系数相加字母及指数不变,可得答案.
【解答】解:A、合并同类项是解题关键,故A错误;
B、不是同类项不能合并,故B错误;
C、不是同类项不能合并,故C错误;
D、合并同类项系数相加字母及指数不变,故D正确;
故选:D.
6.(4分)点C是线段AB的中点,点D是线段AC的三等分点.若线段AB=12cm,则线段BD的长为( )
A.10cmB.8cmC.10cm或8cmD.2cm或4cm
【分析】根据线段中点的定义和线段三等分点的定义即可得到结论.
【解答】解:∵C是线段AB的中点,AB=12cm,
∴AC=BC=AB=×12=6(cm),
点D是线段AC的三等分点,
①当AD=AC时,如图,
BD=BC+CD=BC+AC=6+4=10(cm);
②当AD=AC时,如图,
BD=BC+CD′=BC+AC=6+2=8(cm).
所以线段BD的长为10cm或8cm,
故选:C.
7.(4分)如图,已知直线a∥b,∠1=50°,则∠2的度数为( )
A.140°B.130°C.50°D.40°
【分析】由直线a∥b,利用“两直线平行,同位角相等”可求出∠3的度数,再结合∠2和∠3互补,即可求出∠2的度数.
【解答】解:∵直线a∥b,
∴∠3=∠1=50°.
又∵∠2+∠3=180°,
∴∠2=130°.
故选:B.
8.(4分)下列正方体的展开图上每个面上都有一个汉字.其中,手的对面是口的是( )
A.B.
C.D.
【分析】利用正方体及其表面展开图的特点解题.
【解答】解:A、手的对面是勤,不符合题意;
B、手的对面是口,符合题意;
C、手的对面是罩,不符合题意;
D、手的对面是罩,不符合题意;
故选:B.
9.(4分)已知∠α=60°32′,则∠α的余角是( )
A.29°28′B.29°68′C.119°28′D.119°68′
【分析】根据余角的概念进行计算即可.
【解答】解:∵∠α=60°32′,
∠α的余角是为:90°﹣60°32′=29°28′,
故选:A.
10.(4分)下列说法中正确的是( )
A.﹣a表示负数
B.若|x|=x,则x为正数
C.单项式﹣xy2没有系数
D.多项式7a2b2﹣2ab+1的次数是4
【分析】根据有理数、绝对值、单项式和多项式的概念解答即可.
【解答】解:A、﹣a不一定表示负数,若a=0,则﹣a=0,错误;
B、若|x|=x,则x为非负数,错误;
C、单项式﹣xy2的系数为﹣1,错误;
D、多项式7a2b2﹣2ab+1的次数是4,正确;
故选:D.
11.(4分)中国奇书《易经》中记载,远古时期,人们通过在绳子上打结来计数,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满5进1,用来记录孩子自出生后的天数.由图可知,孩子自出生后的天数是( )
A.10B.89C.165D.294
【分析】根据计数规则可知,从右边第1位的计数单位为50,右边第2位的计数单位为51,右边第3位的计数单位为52,右边第4位的计数单位为53……依此类推,可求出结果.
【解答】解:2×53+1×52+3×51+4×50=294,
故选:D.
12.(4分)如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
A.30°B.20°C.15°D.14°
【分析】延长两三角板重合的边与直尺相交,根据两直线平行,内错角相等求出∠2,再利用三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
【解答】解:如图,∠2=30°,
∠1=∠3﹣∠2=45°﹣30°=15°.
故选:C.
二、填空题:本大题共6个小题,每小题4分,共24分.请将正确答案直接填在答题卡相应的位置上.
13.(4分)用“>”或“<”符号填空:﹣7 > ﹣9.
【分析】根据正数都大于0,负数都小于0,正数大于一切负数.两个负数比较大小,绝对值大的反而小,即可解答.
【解答】解:∵|﹣7|=7,|﹣9|=9,7<9,
∴﹣7>﹣9,
故答案为:>.
14.(4分)若2a3bm与3anb2是同类项,则(m﹣n)2= 1 .
【分析】根据同类项的定义(所含字母相同,相同字母的指数相同)列出方程,求出m,n的值,再代入计算即可.
【解答】解:∵2a3bm与3anb2是同类项,
∴m=2,n=3,
∴(m﹣n)2=(﹣1)2=1.
故答案为:1.
15.(4分)已知a﹣b=3,c+d=2,则(b+c)﹣(a﹣d)的值为 ﹣1 .
【分析】运用整式的加减运算顺序,先去括号,再合并同类项.解答时把已知条件代入即可.
【解答】解:原式=b+c﹣a+d
=c+d﹣a+b
=(c+d)﹣(a﹣b)
=2﹣3=﹣1.
16.(4分)如图,小张从家(图中A处)出发,向南偏东40°的方向走到学校(图中B处)再从学校出发,向北偏西75°的方向走到小明家(图中C处),则∠ABC为 35 度.
【分析】依题意得AE∥DB,利用两直线平行,内错角相等的平行线性质可求出∠DBA=∠EAB,易求∠ABC的度数.
【解答】解:由题意,得DB∥AE,∠DBA=∠EAB=40°,
又∵∠CBD=75°,
∴∠ABC=∠CBD﹣∠DBA=75°﹣40°=35°,
故答案为:35°.
17.(4分)图1是一个正方体的展开图,该正方体从图2所示的位置依次翻到第1格,第2格,第3格,此时小正方体朝上一面的字是 我 .
【分析】根据图1找出相对的两个面,然后按照图2所示的位置动手操作即可解答.
【解答】解:由图1可知:
中与的是相对面,国与我是相对面,梦与梦是相对面,
所以,该正方体从图2所示的位置依次翻到第1格,第2格,第3格,此时小正方体朝上一面的字是:我,
故答案为:我.
18.(4分)我们规定这样一种运算:如果ab=N(a>0,N>0),那么b就叫做以a为底的N的对数,记做b=lgaN.例如:因为23=8,所以lg28=3,那么lg381的值为 4 .
【分析】先把81转化以3为底的幂,再根据有理数的乘方的定义和题目所提供的信息,lg381等于以3为底数81的指数.
【解答】解:∵34=81,
∴lg381=4.
故答案为:4.
三、解答题:本大题共8个小题,共78分.
19.(8分)计算:
(1)﹣14+5﹣(﹣10)+8
(2)﹣22+(﹣)3÷(﹣2)×8
【分析】(1)根据有理数的加减法可以解答本题;
(2)根据有理数的乘方、有理数的乘除法和加法可以解答本题.
【解答】解:(1)﹣14+5﹣(﹣10)+8
=﹣14+5+10+8
=9;
(2)﹣22+(﹣)3÷(﹣2)×8
=﹣4+(﹣)×(﹣)×8
=﹣4+
=﹣.
20.(12分)(1)先化简,再求值:4x2﹣(2x2+x﹣1)+(2﹣2x2﹣3x),其中x=﹣.
(2)如图,∠AOB=60°,∠AOC=90°,OC是∠BOD的平分线,求∠COD的度数.
【分析】(1)先去括号合并同类项进行化简,再将x值代入计算可求解;
(2)由角的和差可求解∠BOC的度数,再利用角平分线的定义可求解∠COD的度数.(1
【解答】解:(1)原式=4x2﹣2x2﹣x+1+2﹣2x2﹣3x
=﹣4x+3;
当x=时,原式=﹣4×()+3=5;
(2)∵∠AOB=60°,∠AOC=90°,
∴∠BOC=∠AOC﹣∠AOB=30°,
又∵OC平分∠BOD,
∴∠COD=∠BOC=30°.
21.(8分)如图,已知直线l和直线外A,B,C三点,按下列要求并作答.
(1)画射线AB;
(2)连接BC;
(3)延长CB至点D,使得BD=BC;
(4)在直线l上确定一点E,使得AE最小,请写出你作图的依据.
【分析】根据射线,线段,垂线段最短解决问题即可.
【解答】解:(1)如图,射线AB即为所求;
(2)如图,线段BC即为所求;
(3)如图,线段BD即为所求;
(4)如图,线段AE即为所求,作图的依据是:垂线段最短.
22.(8分)为了提高足球球员快速抢断转身能力,教练设计了折返跑训练.在足球场上画一条东西方向的直线,如果约定向东为正,向西为负,一组折返跑训练的记录如下(单位:米):40,﹣30,+50,﹣25,+25,﹣30,+15,﹣28,+16,﹣18.
(1)球员最后到达的地方在出发点的哪个方向?距出发点多远?
(2)在这组训练过程中,球员最远处离出发点多远?
(3)球员在这组训练过程中,共跑了多少米?
【分析】(1)根据加法法则,将正数与正数相加,负数与负数相加,进而得出计算得结果;
(2)求出每一段到出发点的距离,即可判断出结果;
(3)利用绝对值的性质以及有理数加法法则求出即可.
【解答】解:(1)∵40﹣30+50﹣25+25﹣30+15﹣28+16﹣18=15(米),
∴球员最后到达的地方在出发点的东边,距出发点15米;
(2)第一次:40;第二次:40﹣30=10;第三次:10+50=60;第四次:60﹣25=35;
第五次:35+25=60;第六次:60﹣30=30;第七次:30+15=45;
第八次:45﹣28=17;第九次:17+16=33;第十次:33﹣18=15;
综上:球员最远处离出发点60米;
(3)∵40+|﹣30|+50+|﹣25|+25+|﹣30|+15+|﹣28|+16+|﹣18|=277(米),
∴共跑了277米.
23.(10分)阅读下列推理过程,在括号中填写理由.
如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°.
试说明:∠GDC=∠B.
解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90° ( 垂直的定义 )
∴EF∥AD ( 同位角相等,两直线平行 )
∴ ∠1 +∠2=180° ( 两直线平行,同旁内角互补 )
又∵∠2+∠3=180°(已知)
∴∠1= ∠3 ( 同角的补角相等 )
∴ AB ∥ DG ( 内错角相等,两直线平行 )
∴∠GDC=∠B ( 两直线平行,同位角相等 )
【分析】根据平行线的性质、判定及垂直、互补等相关概念、定理填空即可.
【解答】解:∵AD⊥BC,EF⊥BC(已知),
∴∠ADB=∠EFB=90° ( 垂直的定义),
∴EF∥AD ( 同位角相等,两直线平行),
∴∠1+∠2=180° ( 两直线平行,同旁内角互补),
又∵∠2+∠3=180°(已知),
∴∠1=∠3( 同角的补角相等),
∴AB∥DG( 内错角相等,两直线平行),
∴∠GDC=∠B ( 两直线平行,同位角相等).
故答案为:垂直的定义;同位角相等,两直线平行;∠1;两直线平行,同旁内角互补;∠3;同角的补角相等;AB;DG;内错角相等,两直线平行;两直线平行,同位角相等.
24.(10分)如图,若干个完全相同的小正方体堆成一个几何体.
(1)请在方格中画出该几何体的左视图和俯视图.
(2)用小立方体搭一个几何体,使得它的左视图和俯视图与你在方格中所画的一致,则这样的几何体最少要 9 个小立方块,最多要 14 个小立方块.
(3)若小正方体的棱长为2cm,请求出图1中几何体的表面积.
【分析】(1)从上面看得到从左往右3列正方形的个数依次为3,2,1,依此画出图形即可;左面看得到从左往右3列正方形的个数依次为3,2,1,依此画出图形即可;
(2)由俯视图易得最底层小立方块的个数,由左视图找到其余层数里最多个数相加即可;
(3)根据正方形面积即可求得表面积.
【解答】解:(1)如图所示:
(2)由俯视图易得最底层有6个小正方体,第二层最少有2个小正方体,第三层最少有1个小正方体,所以最少有6+2+1=9个小正方体;
由俯视图易得最底层有6个小正方体,第二层最多有5个小正方体,第三层最多有3个小正方体,所以最多有6+5+3=14个小正方体.
故答案为:9;14;
(3)这个几何体的表面积为:(6×2+6×2+6×2)×22=144cm2.
25.(10分)根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从2017年5月1日起对居民生活用电实施“阶梯电价”收费,具体收费标准见下表:
实施“阶梯电价”收费以后,该市居民陈先生家积极响应号召节约用电,2019年10月用电100千瓦时,交电费50元.
(1)求上表中a的值.
(2)陈先生家2019年11月用电200千瓦时,应交费多少元?
(3)若陈先生家2019年12月份的用电量为x千瓦时(x>150),请用含x的代数式表示陈先生一家应交多少元电费.
【分析】(1)由单价=,可得;
(2)由电费=不超过150千瓦的电费+超过150千瓦的部分,列式可求解;
【解答】解:(1)∵100<150,
∴.
(2)∵150<200<300,
∴应交150×0.5+(200﹣150)×0.6=75+30=105(元).
(3)①当x>300时,应交150×0.5+(300﹣150)×0.6+(x﹣300)×(0.5+0.3)=75+90+0.8(x﹣300)=(0.8x﹣75)元.
②当150<x≤300时,应交150×0.5+(x﹣150)×0.6=75+0.6x﹣90=(0.6x﹣15)元,
综上:若150<x≤300,应交(0.6x﹣15)元,
若x>300,应交(0.8x﹣75)元.
26.(12分)如图,已知点C在线段AB上,线段AC=12厘米,BC=8厘米,点M,N分别是AC,BC的中点.
(1)求线段MN的长;
(2)根据第(1)题的计算过程和结果,设AC+BC=a,其它条件不变,直接写出MN的长度;
(3)动点P、Q分别从A,B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿BA向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动,设运动时间为x秒,是否存在某一时刻,使得C、P、Q这三个点中,有一个点恰为另外两点所连线段的中点?若存在,求出所有满足条件的x的值;若不存在,请说明理由.
【分析】(1)由M是AC的中点,N是BC的中点,可得MN=MC+CN=(AC+BC)=AB,即可得答案;
(2)同(1)可得MN=a;
(3)分三种情况:当C为PQ的中点时,可得12﹣2x=8﹣x,当P为CQ的中点时,可得2x﹣12=20﹣3x,当Q为PC的中点时,可得2(8﹣x)=2x﹣12,即可解得答案.
【解答】解:(1)∵M是AC的中点,
∴MC=AC,
∵N是BC的中点,
∴CN=BC,
∴MN=MC+CN=(AC+BC)=AB=10(厘米);
(2)∵M是AC的中点,
∴MC=AC,
∵N是BC的中点,
∴CN=BC,
∴MN=MC+CN=(AC+BC)=AB=a;
(3)存在某一时刻,使得C、P、Q这三个点中,有一个点恰为另外两点所连线段的中点,
当C为PQ的中点时,12﹣2x=8﹣x,
解得:x=4;
当P为CQ的中点时,2x﹣12=20﹣3x,
解得:x=6.4;
当Q为PC的中点时,2(8﹣x)=2x﹣12,
解得:x=7;
综上所述,当x为4或6.4或7时,C、P、Q这三个点中,有一个点恰为另外两点所连线段的中点.
一户居民一个月用电量的范围
电费价格(单位:元/千瓦时)
不超过150千瓦时的部分
a
超过150千瓦时,但不超过300千瓦时的部分
0.6
超过300千瓦时的部分
a+0.3
一户居民一个月用电量的范围
电费价格(单位:元/千瓦时)
不超过150千瓦时的部分
a
超过150千瓦时,但不超过300千瓦时的部分
0.6
超过300千瓦时的部分
a+0.3
2023年四川省眉山市丹棱县中考数学适应性试卷(含解析): 这是一份2023年四川省眉山市丹棱县中考数学适应性试卷(含解析),共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年四川省眉山市丹棱县九上数学期末质量检测试题含答案: 这是一份2023-2024学年四川省眉山市丹棱县九上数学期末质量检测试题含答案,共8页。试卷主要包含了已知关于x的一元二次方程x2+等内容,欢迎下载使用。
2022-2023学年四川省眉山市仁寿县七年级(上)期末数学试卷(含解析): 这是一份2022-2023学年四川省眉山市仁寿县七年级(上)期末数学试卷(含解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













