初中数学冀教版八年级下册第二十一章 一次函数综合与测试精练

这是一份初中数学冀教版八年级下册第二十一章 一次函数综合与测试精练，共31页。试卷主要包含了若一次函数，若实数，下列不能表示是的函数的是等内容，欢迎下载使用。
八年级数学下册第二十一章一次函数同步训练
考试时间：90分钟；命题人：数学教研组
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、如图，点P是▱ABCD边上一动点，沿A→D→C→B的路径移动，设P点经过的路径长为x，△BAP的面积是y，则下列能大致反映y与x的函数关系的图象是（ ）

A． B．
C． D．
2、在平面直角坐标系中，已知点，点，在x轴上确定点C，使得的周长最小，则点C的坐标是（ ）
A． B． C． D．
3、下列函数中，y是x的一次函数的是（　　）
A．y＝ B．y＝﹣3x+1 C．y＝2 D．y＝x2+1
4、关于函数y＝－2x＋1，下列结论正确的是（ ）
A．图像经过点 B．y随x的增大而增大
C．图像不经过第四象限 D．图像与直线y＝－2x平行
5、若一次函数（，为常数，）的图象不经过第三象限，那么，应满足的条件是（ ）
A．且 B．且
C．且 D．且
6、若实数、满足且，则关于的一次函数的图像可能是（ ）
A． B． C． D．
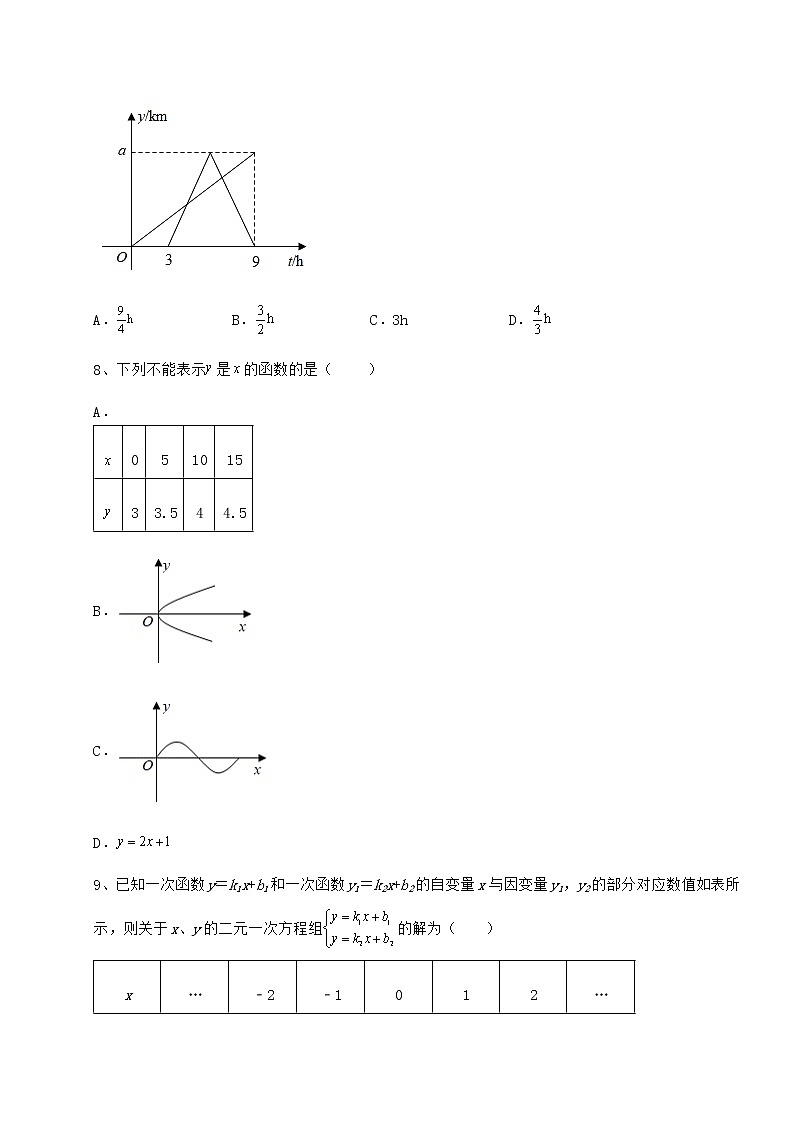
7、一辆快车和一辆慢车将一批物资从甲地运往乙地，其中快车送达后立即沿原路返回，且往返速度的大小不变，两车离甲地的距离y（单位：km）与慢车行驶时间t（单位：h）的函数关系如图，则两车先后两次相遇的间隔时间是（ ）

A． B． C．3h D．
8、下列不能表示是的函数的是（ ）
A．

0
5
10
15

3
3.5
4
4.5
B．
C．
D．
9、已知一次函数y＝k1x+b1和一次函数y1＝k2x+b2的自变量x与因变量y1，y2的部分对应数值如表所示，则关于x、y的二元一次方程组的解为（　　）
x
…
﹣2
﹣1
0
1
2
…
y1
…
﹣1
0
1
2
3
…
y2
…
﹣5
﹣3
﹣1
1
3
…
A． B． C． D．
10、下列问题中，两个变量成正比例的是（　　）
A．圆的面积S与它的半径r
B．三角形面积一定时，某一边a和该边上的高h
C．正方形的周长C与它的边长a
D．周长不变的长方形的长a与宽b
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、直线l1：y＝x+1与直线l2：y＝mx+n相交于点P（a，2），则关于x的不等式x+1≥mx+n的解集为_____．

2、在直角坐标系中，等腰直角三角形、、、、按如图所示的方式放置，其中点、、、、均在一次函数的图象上，点、、、、均在轴上．若点的坐标为，点的坐标为，则点的坐标为___．

3、直线y=2x-4与两坐标轴围成的三角形面积为___________________．
4、已知函数是关于x的一次函数，则______．
5、下列函数：①；②；③；④；⑤．其中一定是一次函数的有____________．（只是填写序号）
三、解答题（5小题，每小题10分，共计50分）
1、已知y与x﹣2成正比例，且当x＝1时，y＝﹣2

(1)求变量y与x的函数关系式；
(2)请在给出的平面直角坐标系中画出此函数的图象；
(3)已知点A在函数y＝ax＋b的图象上，请直接写出关于x的不等式ax＋b＞2x﹣4的解集　 　．
2、在平面直角坐标系xOy中，对于线段AB和点C，若△ABC是以AB为一条直角边，且满足AC>AB的直角三角形，则称点C为线段AB的“关联点”，已知点A的坐标为（0，1）．

(1)若B（2，1），则点D（3，1），E（2，0），F（0，-3），G（-1，-2）中，是AB关联点的有_______；
(2)若点B（-1，0），点P在直线y=2x-3上，且点P为线段AB的关联点，求点P的坐标；
(3)若点B（b，0）为x轴上一动点，在直线y=2x+2上存在两个AB的关联点，求b的取值范围．
3、为巩固拓展脱贫攻坚成果，开启乡村振兴发展之门，某村村民组长组织村民加工板栗并进行销售．根据现有的原材料，预计加工规格相同的普通板栗、精品板栗共4000件．某天上午的销售件数和所卖金额统计如下表：

普通板栗（件）
精品板栗（件）
总金额（元）
甲购买情况
2
3
350
乙购买情况
4
1
300
(1)求普通板栗和精品板栗的单价分别是多少元．
(2)根据（1）中求出的单价，若普通板栗和精品板栗每件的成本分别为40元、60元，且加工普通板栗a件（），则4000件板栗的销售总利润为w元．问普通板栗和精品板栗各加工多少件，所获总利润最多？最多总利润是多少？
4、如图是某种蜡烛在燃烧过程中高度与时间之间关系的图象，由图象解答下列问题：

(1)求蜡烛在燃烧过程中高度与时间之间的函数表达式
(2)经过多少小时蜡烛燃烧完毕？
5、为加快“智慧校园”建设，某市准备为试点学校采购一批A、B两种型号的一体机．经过市场调查发现，今年每套B型一体机的价格比每套A型一体机的价格多0.6万元，且用960万元恰好能购买500套A型一体机和200套B型一体机．
(1)求今年每套A型、B型一体机的价格各是多少万元？
(2)该市明年计划采购A型、B型一体机共1100套，考虑物价因素，预计明年每套A型一体机的价格比今年上涨25%，若购买B型一体机的总费用不低于购买A型一体机的总费用，那么该市明年至少需要投入多少万元才能完成采购计划？

-参考答案-
一、单选题
1、A
【解析】
【分析】
分三段来考虑点P沿A→D运动，的面积逐渐变大；点P沿D→C移动，的面积不变；点P沿C→B的路径移动，的面积逐渐减小，同时考虑各段的函数解析式，据此选择即可得．
【详解】
解：如图，过点B作BH⊥DA交DA的延长线于H，设BH＝h，则当点P在线段AD上时，，h是定值，y是x的一次函数，

点P沿A→D运动，的面积逐渐变大，且y是x的一次函数，
点P沿D→C移动，的面积不变，
点P沿C→B的路径移动，的面积逐渐减小，同法可知y是x的一次函数，
故选：A．
【点睛】
本题以动点问题为背景，考查了分类讨论的数学思想以及函数图象的变化规律，理解题意，作出辅助线是解题关键．
2、C
【解析】
【分析】
因为AB的长度是确定的，故△CAB的周长最小就是CA+CB的值最小，作点A关于x轴的对称点A′，连接A′B交x轴于点C，求出C点坐标即可．
【详解】
解：如图，作点A关于x轴的对称点A′，连接A′B交x轴于点C，此时，AC+BC=A′C+BC=AC，长度最小，
∵A（-1，2），
∴A′（-1，﹣2），
设直线A′B的解析式为y＝kx+b（k≠0），把A′（-1，﹣2），代入得，
∴，解得，
∴直线A′B的解析式为y＝-2x﹣4，
当y＝0时，x＝-2，
∴C（-2，0）．
故选：C

【点睛】
本题考查了轴对称-最短路径问题，一次函数与坐标轴交点问题，解题关键是确定点C的位置，利用一次函数解析式求坐标．
3、B
【解析】
【分析】
利用一般地，形如y=kx+b（k≠0，k、b是常数）的函数，叫做一次函数，进而判断得出答案．
【详解】
解：∵y＝不符合一次函数的形式，故不是一次函数，
∴选项A不符合题意；
∵形如y＝kx+b（k，b为常数）．
∴y＝﹣3x+1中，y是x的一次函数．
故选项B符合题意；
∵y＝2是常数函数，
∴选项C不符合题意；
∵y＝x2+1不符合一次函数的形式，故不是一次函数，
∴选项D不符合题意；
综上，y是x的一次函数的是选项B．
故选：B．
【点睛】
本题主要考查了一次函数的定义，正确把握一次函数的定义是解题关键．
4、D
【解析】
【分析】
根据一次函数的性质对各选项进行逐一判断即可．
【详解】
解：A、当x＝−2，y＝−2x＋1＝−2×（−2）＋1＝5，则点（−2，1）不在函数y＝−2x＋1图象上，故本选项错误；
B、由于k＝−2＜0，则y随x增大而减小，故本选项错误；
C、由于k＝−2＜0，则函数y＝−2x＋1的图象必过第二、四象限，b＝1＞0，图象与y轴的交点在x的上方，则图象还过第一象限，故本选项错误；
D、由于直线y＝−2x＋1与直线y＝−2x的倾斜角相等且与y轴交于不同的点，所以它们相互平行，故本选项正确；
故选：D．
【点睛】
本题考查了一次函数y＝kx＋b（k≠0）的性质：当k＞0，图象经过第一、三象限，y随x增大而增大；当k＜0，图象经过第二、四象限，y随x增大而减小；当b＞0，图象与y轴的交点在x的上方；当b＝0，图象经过原点；当b＜0，图象与y轴的交点在x的下方．
5、D
【解析】
【分析】
根据一次函数图象与系数的关系解答即可．
【详解】
解：一次函数、是常数，的图象不经过第三象限，
且，
故选：D．
【点睛】
本题主要考查了一次函数图象与系数的关系，直线y=kx+b所在的位置与k、b的符号有直接的关系为：k＞0时，直线必经过一、三象限．k＜0时，直线必经过二、四象限．b＞0时，直线与y轴正半轴相交．b=0时，直线过原点；b＜0时，直线与y轴负半轴相交．
6、B
【解析】
【分析】
根据实数、满足可知，、互为相反数，再根据，可确定、的符号，进而确定图象的大致位置．
【详解】
解：∴实数、满足，
∴、互为相反数，
∵，
∴，，
∴
∴一次函数的图像经过二、三、四象限，
故选：B．
【点睛】
本题考查了一次函数图象的性质，解题关键是根据已知条件，确定、的符号．
7、A
【解析】
【分析】
根据图象得出，慢车的速度为 km/h，快车的速度为 km/h．从而得出快车和慢车对应的y与t的函数关系式．联立两个函数关系式，求解出图象对应两个交点的坐标，即可得出间隔时间．
【详解】
解：根据图象可知，慢车的速度为 km/h．
对于快车，由于往返速度大小不变，总共行驶时间是6h，
因此单程所花时间为3 h，故其速度为 km/h．
所以对于慢车，y与t的函数表达式为y＝t (0≤t≤9)①．
对于快车，y与t的函数表达式为
y=，
联立①②，可解得交点横坐标为t=4.5，
联立①③，可解得交点横坐标为t=，
因此，两车先后两次相遇的间隔时间是，
故选：A．
【点睛】
本题主要考查根据函数图象求一次函数表达式，以及求两个一次函数的交点坐标．解题的关键是利用图象信息得出快车和慢车的速度，进而写出y与t的关系．
8、B
【解析】
【分析】
根据函数的定义（如果有两个变量x和y，并且对于x的每一个确定的值，y都有唯一确定的值与其对应，我们就把x称为自变量，把y称为因变量，y是x的函数）及利用待定系数法确定一次函数解析式依次进行判断即可得．
【详解】
解：A、根据图表进行分析为一次函数，设函数解析式为：，
将，，，
分别代入解析式为：
，
解得：，，
所以函数解析式为：，
∴y是x的函数；
B、从图象上看，一个x值，对应两个y值，不符合函数定义，y不是x的函数；
C、D选项从图象及解析式看可得y是x的函数．
故选：B．
【点睛】
题目主要考查函数的定义及利用待定系数法确定一次函数解析式，深刻理解函数定义是解题关键．
9、C
【解析】
【分析】
利用方程组的解就是两个相应的一次函数图象的交点坐标解决问题．
【详解】
解：由表格可知，一次函数y1=k1x+b1和一次函数y2=k2x+b2的图象都经过点(2，3)，
∴一次函数y1=k1x与y=k2x+b的图象的交点坐标为(2，3)，
∴关于x，y的二元一次方程组的解为．
故选：C．
【点睛】
本题考查了一次函数图像交点坐标与方程组解的关系：对于函数y1=k1x+b1，y2=k2x+b2，其图象的交点坐标(x，y)中x，y的值是方程组的解．
10、C
【解析】
【分析】
分别列出每个选项两个变量的函数关系式，再根据函数关系式逐一判断即可.
【详解】
解： 所以圆的面积S与它的半径r不成正比例，故A不符合题意；
所以三角形面积一定时，某一边a和该边上的高h不成正比例，故B不符合题意；
所以正方形的周长C与它的边长a成正比例，故C符合题意；

所以周长不变的长方形的长a与宽b不成正比例，故D不符合题意；
故选C
【点睛】
本题考查的是两个变量成正比例，掌握“正比例函数的特点”是解本题的关键.
二、填空题
1、x≥1
【解析】
【分析】
将P(a，2)代入直线l1：y＝x+1中求出a＝1，然后再根据图像越在上方，其对应的函数值越大即可求解．
【详解】
解：将点P(a，2)坐标代入直线y＝x+1，得a＝1，
从图中直接看出，在P点右侧时，直线l1：y＝x+1在直线l2：y＝mx+n的上方，
即当x≥1时，x+1≥mx+n，
故答案为：x≥1．
【点睛】
本题考查了一元一次不等式与一次函数的关系，图像越在上方，其对应的函数值就越大．
2、
【解析】
【分析】
首先，根据等腰直角三角形的性质求得点A1、A2的坐标；然后，将点A1、A2的坐标代入一次函数解析式，利用待定系数法求得该直线方程是y=x+1；最后，利用等腰直角三角形的性质推知点Bn-1的坐标，然后将其横坐标代入直线方程y=x+1求得相应的y值，从而得到点An的坐标．
【详解】
解：如图，点的坐标为，点的坐标为，
，，则．
△是等腰直角三角形，，
．
点的坐标是．
同理，在等腰直角△中，，，则．
点、均在一次函数的图象上，
，解得，，
该直线方程是．
点，的横坐标相同，都是3，
当时，，即，则，
．
同理，，

，，
当时，，
即点的坐标为，．
故答案为，．

【点睛】
本题考查了一次函数图象上点的坐标特点，涉及到的知识点有待定系数法求一次函数解析式，一次函数图象上点的坐标特征以及等腰直角三角形的性质．解答该题的难点是找出点Bn的坐标的规律．
3、
【解析】
【分析】
画出一次函数的图象，再求解一次函数与坐标轴的交点的坐标，再利用三角形的面积公式进行计算即可.
【详解】
解：如图，令 则
令 则 解得



故答案为：4
【点睛】
本题考查的是一次函数与坐标轴的交点坐标，一次函数与坐标轴围成的三角形的面积，利用数形结合的方法解题是解本题的关键.
4、4
【解析】
【分析】
由一次函数的定义可知x的次数为1，即3-m=1，x的系数不为0，即，然后对计算求解即可．
【详解】
解：由题意知
解得（舍去），
故答案为：4．
【点睛】
本题考查了一次函数，绝对值方程，解不等式．解题的关键根据一次函数的定义求解参数．
5、②③⑤
【解析】
【分析】
根据一次函数的定义条件解答即可．
【详解】
解：①y＝kx当k＝0时原式不是一次函数；
②是一次函数；
③由于＝x，则是一次函数；
④y＝x2＋1自变量次数不为1，故不是一次函数；
⑤y＝22−x是一次函数．
故答案为：②③⑤．
【点睛】
本题主要考查了一次函数的定义，一次函数y＝kx＋b的定义条件是：k、b为常数，k≠0，自变量次数为1．
三、解答题
1、 (1)y＝2x﹣4
(2)见解析
(3)x＜3
【解析】
【分析】
（1）设y＝k（x﹣2）（k为常数，k≠0），把x＝1，y＝﹣2代入得：﹣2＝k（1﹣2），求出k＝2即可；
（2）列表描点连线即可；
（3）先确定A点的坐标是（3，2），把A点的横坐标代入y＝2x﹣4求出函数值=2，即点A也在函数y＝2x﹣4的图象上，点A是函数y＝ax+b和函数y＝2x﹣4的交点，然后利用图像法求不等式的解集即可．
(1)
解：∵y与x﹣2成正比例，
∴设y＝k（x﹣2）（k为常数，k≠0），
把x＝1，y＝﹣2代入得：﹣2＝k（1﹣2），
解得：k＝2，
即y＝k（x﹣2）＝2（x﹣2）＝2x﹣4，
所以变量y与x的函数关系式是y＝2x﹣4；
(2)
列表
x
0
2
y
-4
0
描点（0，-4），（2，0），
连线得y＝2x﹣4的图象；

(3)
从图象可知：A点的坐标是（3，2），把A点的横坐标x=3代入y＝2x﹣4时，y=2，
即点A也在函数y＝2x﹣4的图象上，
即点A是函数y＝ax+b和函数y＝2x﹣4的交点，
∴关于x的不等式ax+b＞2x﹣4反应在函数图像函数y＝ax+b在函数y＝2x﹣4图像上方，交点A的左侧，
所以关于x的不等式ax+b＞2x﹣4的解集是x＜3，
故答案为：x＜3．
【点睛】
本题考查待定系数法求函数解析式，描点法画函数图像，用图像法求不等式的解集，掌握待定系数法求函数解析式，描点法画函数图像，用图像法求不等式的解集是解题关键．
2、 (1)点E，点F；
(2)（）或（）；
(3)b的取值范围1＜b＜2或2＜b＜3．
【解析】
【分析】
（1）根据以点B为直角顶点，点B与点E横坐标相同，点E在过点B与AB垂直的直线上，△ABE为直角三角形，且AE大于AB；以点A为直角顶点，点A与点F横坐标相同，△AFB为直角三角形，BF大于AB即可；
（2）根据点A（0，1）点B（-1，0），OA=OB，∠AOB=90°，得出△AOB为等腰直角三角形，可得∠ABO=∠BAO=45°，以点A为直角顶点，过点A，与AB垂直的直线交x轴于S，利用待定系数法求出AS解析式为，联立方程组，以点B为直角顶点，过点B，与AB垂直的直线交y轴于R，∠OBR=90°-∠ABO=45°，可得△OBR为等腰直角三角形，OR=OB=1，点R（0，-1），利用平移的性质可求BR解析式为，联立方程组，解方程组即可；
（3）过点A与AB垂直的直线交直线y=2x+2于U，把△AOB绕点A顺时针旋转90°，得△AO′U，AO′=AO=1，O′U=OB=b，根据点U（-1，b-1）在直线上，得出方程，求出b的值，当过点A的直线与直线平行时没有 “关联点”，OB=OW=b=2，得出在1＜b＜2时，直线上存在两个AB的“关联点”，当b＞2时，根据旋转性质将△AOB绕点A逆时针旋转90°得到△AO′U，得出AO′=AO=1，O′U=OB=b，根据点U（1,1+b）在直线上，列方程，得出即可．
(1)
解：点D与AB纵坐标相同，在直线AB上，不能构成直角三角形，
以点B为直角顶点，点B与点E横坐标相同，点E在过点B与AB垂直的直线上，
∴△ABE为直角三角形，且AE大于AB；

以点A为直角顶点，点A与点F横坐标相同，△AFB为直角三角形，AF=4＞AB=2，

∴点E与点F是AB关联点，
点G不在A、B两点垂直的直线上，故不能构成直角三角形，
故答案为点E，点F；
(2)
解：∵点A（0，1）点B（-1，0），OA=OB，∠AOB=90°，
∴△AOB为等腰直角三角形，AB=
∴∠ABO=∠BAO=45°，
以点A为直角顶点，过点A，与AB垂直的直线交x轴于S，
∴∠OAS=90°-∠BAO=45°，
∴△AOS为等腰直角三角形，
∴OS=OA=1，点S（1,0），
设AS解析式为代入坐标得：
，
解得，
AS解析式为，
∴，
解得，
点P（），
AP=，AP＞AB
以点B为直角顶点，过点B，与AB垂直的直线交y轴于R，
∴∠OBR=90°-∠ABO=45°，
∴△OBR为等腰直角三角形，
∴OR=OB=1，点R（0，-1），
过点R与AS平行的直线为AS直线向下平移2个单位，
则BR解析式为，
∴，
解得，
点P1（），
AP1=＞，
∴点P为线段AB的关联点，点P的坐标为（）或（）；

(3)
解：过点A与AB垂直的直线交直线y=2x+2于U，
把△AOB绕点A顺时针旋转90°，得△AO′U，
∴AO′=AO=1，O′U=OB=b，
点U（-1，b-1）在直线上，
∴
∴，
∴当b＞1时存在两个“关联点”，
当b＜1时，UA＜AB，不满足定义，没有两个“关联点”

当过点A的直线与直线平行时没有 “关联点”
与x轴交点X（-1，0），与y轴交点W（0，2）
∵OA=OX=1,∠XOW=∠AOB=90°，AB⊥XW，
∴△OXW顺时针旋转90°，得到△OAB，
∴OB=OW=2，
∴在1＜b＜2时，直线上存在两个AB的“关联点”，

当b＞2时，将△AOB绕点A逆时针旋转90°得到△AO′U，
∴AO′=AO=1，O′U=OB=b，
点U（1,1+b）在直线上，
∴
∴解得
∴当2＜b＜3时, 直线上存在两个AB的“关联点”，
当b＞3时，UA＜AB，不满足定义，没有两个“关联点”

综合得，b的取值范围1＜b＜2或2＜b＜3．
【点睛】
本题考查新定义线段的意义，直角三角形性质，仔细阅读新定义，由两个条件，（1）组成直角三角形，（2）AC＞AB，等腰直角三角形，勾股定理两点距离公式，待定系数法求直线解析式，图形旋转，两函数交点联立方程组，掌握新定义线段的意义，直角三角形性质，仔细阅读新定义，由两个条件，（1）组成直角三角形，（2）AC＞AB，等腰直角三角形，勾股定理两点距离公式，待定系数法求直线解析式，图形旋转，两函数交点联立方程组，是解题关键．
3、 (1)普通板栗的单价为55元，精品板栗的单价为80元；
(2)普通板栗加工1000件，精品板栗加工3000件，所获总利润最多，最多总利润是75000元．
【解析】
【分析】
（1）设普通板栗的单价为x元，精品板栗的单价为y元，根据表格列出二元一次方程组，求解即可得；
（2）加工普通板栗a件，则加工精品板栗(4000-a)件，根据题意可得利润的函数关系式，根据一次函数的性质及自变量的取值范围可得当时，所获总利润w最多，代入求解即可得．
(1)
解：设普通板栗的单价为x元，精品板栗的单价为y元，由题意得：
，
解得x=55y=80，
答：普通板栗的单价为55元，精品板栗的单价为80元；
(2)
解：加工普通板栗a件，则加工精品板栗(4000-a)件，
由题意得：，
∵，1000≤a≤3000，
∴当时，所获总利润w最多，
w=-5×1000+80000=75000，
∴，
答：普通板栗加工1000件，精品板栗加工3000件，所获总利润最多，最多总利润是75000元．
【点睛】
题目主要考查二元一次方程组的应用及一次函数的最大利润问题，理解题意，列出方程及函数解析式是解题关键．
4、 (1)y=-8x+15（0≤x≤）
(2)小时
【解析】
【分析】
（1）由图象可知一次函数过（0，15），（1，7）两点，可根据待定系数法列方程，求函数关系式．
（2）将y=0的值代入，求x的解，即为蜡烛全部燃烧完所用的时间；
(1)
由图象可知过（0，15），（1，7）两点，
设一次函数表达式为y=kx+b，
∴，
解得，
∴此一次函数表达式为：y=-8x+15（0≤x≤）．
(2)
令y=0
∴-8x+15=0
解得：x＝，
答：经过小时蜡烛燃烧完毕．
【点睛】
本题考查了用待定系数法求一次函数关系式，并会用一次函数研究实际问题，具备在直角坐标系中的读图能力．
5、 (1)今年每套A型一体机的价格为1.2万元，每套B型一体机的价格为1.8万元
(2)1800万
【解析】
【分析】
（1）设今年每套A型一体机的价格为x万元，每套B型一体机的价格为y万元，根据题意列出二元一次方程组，解方程组求解即可；
（2）设该市明年购买A型一体机m套，则购买B型一体机（1100-m）套，列出一元一次不等式组求得的范围，进而设明年需投入W万元，根据题意列出关于的关系式，根据一次函数的性质求得最小值即可求解．
(1)
设今年每套A型一体机的价格为x万元，每套B型一体机的价格为y万元，
由题意得：，
解得：
答：今年每套A型一体机的价格为1.2万元，每套B型一体机的价格为1.8万元；
(2)
设该市明年购买A型一体机m套，则购买B型一体机（1100-m）套，
由题意可得：1.8（1100-m）≥1.2（1+25%）m，
解得：m≤600，
设明年需投入W万元，
W=1.2×（1+25%）m+1.8（1100-m）
=-0.3m+1980，
∵-0.3＜0，
∴W随m的增大而减小，
∵m≤600，
∴当m=600时，W有最小值-0.3×600+1980=1800，
故该市明年至少需投入1800万元才能完成采购计划．
【点睛】
本题考查了二元一次方程组的应用，一元一次不等式的应用，一次函数的应用，根据题意列出二元一次方程组、不等式以及一次函数关系式是解题的关键．