

初中数学冀教版八年级下册第二十一章 一次函数综合与测试同步练习题
展开
这是一份初中数学冀教版八年级下册第二十一章 一次函数综合与测试同步练习题,共22页。试卷主要包含了下列函数中,属于正比例函数的是等内容,欢迎下载使用。
八年级数学下册第二十一章一次函数专题测试 考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、某工厂投入生产一种机器,每台成本y(万元/台)与生产数量x(台)之间是函数关系,函数y与自变量x的部分对应值如表:则y与x之间的解析式是( )x(单位:台)102030y(单位:万元/台)605550A.y=80- 2x B.y=40+ 2xC.y=65- D.y=60-2、如图,在Rt△ABO中,∠OBA=90°,A(4,4),且,点D为OB的中点,点P为边OA上的动点,使四边形PDBC周长最小的点P的坐标为( )A.(2,2) B.(,) C.(,) D.(,)3、已知点和点在一次函数的图象上,且,下列四个选项中k的值可能是( )A.-3 B.-1 C.1 D.34、AB两地相距20km,甲从A地出发向B地前进,乙从B地出发向A地前进,两人沿同一直线同时出发,甲先以8km/h的速度前进1小时,然后减慢速度继续匀速前进,甲乙两人离A地的距离s(km)与时间t(h)的关系如图所示,则甲出发( )小时后与乙相遇.A.1.5 B.2 C.2.5 D.35、小豪骑自行车去位于家正东方向的书店买资料用于自主复习.小豪离家5min后自行车出现故障,小豪立即打电话给爸爸,让爸爸带上工具箱从家里来帮忙维修(小豪和爸爸通话以及爸爸找工具箱的时间忽略不计),同时小豪以原来速度的一半推着自行车继续向书店走去,爸爸接到电话后,立刻出发追赶小豪,追上小豪后,爸爸用2min的时间修好了自行车,并立刻以原速到位于家正西方500m的公司上班,小豪则以原来的骑车速度继续向书店前进,爸爸到达公司时,小豪还没有到达书店.如图是小豪与爸爸的距离y(m)与小豪的出发时间x(min)之向的函数图象,请根据图象判断下列哪一个选项是正确的( ) A.小豪爸爸出发后12min追上小豪 B.小李爸爸的速度为300m/minC.小豪骑自行车的速度为250m/min D.爸爸到达公司时,小豪距离书店500m6、已知点,都在直线上,则与的大小关系为( )A. B. C. D.无法比较7、在平面直角坐标系中,正比例函数y =kx(k<0)的图象的大致位置只可能是( )A. B.C. D.8、甲、乙两地之间是一条直路,在全民健身活动中,王明跑步从甲地往乙地,陈启浩骑自行车从乙地往甲地,两人同时出发,陈启浩先到达目的地,两人之间的距离s(km)与运动时间t(h)的函数关系大致如图所示,下列说法中错误的是( )A.两人出发1小时后相遇B.王明跑步的速度为8km/hC.陈启浩到达目的地时两人相距10kmD.陈启浩比王明提前1.5h到目的地9、下列函数中,属于正比例函数的是( )A. B. C. D.10、已知点(﹣1,y1),(4,y2)在一次函数y=3x+a的图象上,则y1,y2的大小关系是( )A.y1<y2 B.y1=y2 C.y1>y2 D.不能确定第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、已知 M(1, a )和 N(2, b )是一次函数 y=-x+1 图像上的两点,则 a______b (填“>”、“<”或“=”).2、已知直线y=kx+b(k≠0)的图像与直线y=-2x平行,且经过点(2,3),则该直线的函数表达式为______________________.3、当k>0时,直线y=kx+b由左到右逐渐______,y随x的增大而______.① b>0时,直线经过第______象限;② b<0时,直线经过第______ 象限. 当k<0时,直线y=kx+b由左到右逐渐______,y随x的增大而______.①b>0时,直线经过第______象限;② b<0时,直线经过第______象限.4、如图,一次函数和的图象交于点,则不等式的解集是______.5、观察图象可知:当k>0时,直线y=kx+b从左向右______;当k<0时,直线y=kx+b从左向右______.由此可知,一次函数y=kx+b(k,b是常数,k≠0) 具有如下性质:当k>0时,y随x的增大而______;当k<0时,y随x的增大而______.三、解答题(5小题,每小题10分,共计50分)1、某校计划为在校运会上表现突出的12名志愿者每人颁发一件纪念品,李老师前往购买钢笔和笔记本作为纪念品,如果买10支钢笔和2本笔记本,需230元;如果买8支钢笔和4本笔记本,需220元.(1)求钢笔和笔记本的单价;(2)售货员提示:当购买的钢笔超过6支时,所有的钢笔打9折.设购买纪念品的总费用为w元,其中钢笔的支数为a.①当时,求w与a之间的函数关系式;②李老师购买纪念品一共花了210元钱,他可能购买了多少支钢笔?2、已知一次函数y1=ax+b,y2=bx+a(ab≠0,且a≠b).(1)若y1过点(1,2)与点(2,b﹣a﹣3)求y1的函数表达式;(2)y1与y2的图象交于点A(m,n),用含a,b的代数式表示n;(3)设y3=y1﹣y2,y4=y2﹣y1,当y3>y4时,求x的取值范围.3、A、B两地相距20千米,甲、乙两人某日中午12点同时从A地出发匀速前往B地,甲的速度是每小时4千米,如图,线段OM反映了乙所行的路程s与所用时间t之间的函数关系,根据提供的信息回答下列问题:(1)乙由A地前往B地所行的路程s与所用时间t之间的函数解析式是 ,定义域是 ;(2)在图中画出反映甲所行驶的路程s与所用时间t之间的函数图象;(3)下午3点时,甲乙两人相距 千米.4、已知一次函数的图象经过点和.(1)求此一次函数的表达式;(2)点是否在直线AB上,请说明理由.5、经开区某中学计划举行一次知识竞赛,并对获奖的同学给予奖励.现要购买甲、乙两种奖品,已知1件甲种奖品和2件乙种奖品共需40元,2件甲种奖品和3件乙种奖品共需70元.(1)求甲、乙两种奖品的单价;(2)根据颁奖计划,该中学需甲、乙两种奖品共60件,且甲种奖品不少于乙种奖品的一半,应如何购买才能使总费用最少?并求出最少费用. -参考答案-一、单选题1、C【解析】略2、C【解析】【分析】先确定点D关于直线AO的对称点E(0,2),确定直线CE的解析式,直线AO的解析式,两个解析式的交点就是所求.【详解】∵∠OBA=90°,A(4,4),且,点D为OB的中点,∴点D(2,0),AC=1,BC=3,点C(4,3),设直线AO的解析式为y=kx,∴4=4k,解得k=1,∴直线AO的解析式为y=x,过点D作DE⊥AO,交y轴于点E,交AO于点F,∵∠OBA=90°,A(4,4),∴∠AOE=∠AOB=45°,∴∠OED=∠ODE=45°,OE=OD,∴DF=FE,∴点E是点D关于直线AO的对称点,∴点E(0,2),连接CE,交AO于点P,此时,点P是四边形PCBD周长最小的位置,设CE的解析式为y=mx+n,∴,解得,∴直线CE的解析式为y=x+2,∴,解得,∴使四边形PDBC周长最小的点P的坐标为(,),故选C.【点睛】本题考查了一次函数的解析式,将军饮马河原理,熟练掌握待定系数法和将军饮马河原理是解题的关键.3、A【解析】【分析】由m-1<m+1时,y1>y2,可知y随x增大而减小,则比例系数k+2<0,从而求出k的取值范围.【详解】解:当m-1<m+1时,y1>y2,y随x的增大而减小,∴k+2<0,得k<﹣2.故选:A.【点睛】本题考查一次函数的图象性质:当k<0,y随x增大而减小,难度不大.4、B【解析】【分析】根据题意结合图象分别求出甲减速后的速度已经乙的速度,再列方程解答即可.【详解】解:甲减速后的速度为:(20﹣8)÷(4﹣1)=4(km/h),乙的速度为:20÷5=4(km/h),设甲出发x小时后与乙相遇,根据题意得8+4(x﹣1)+4x=20,解得x=2.即甲出发2小时后与乙相遇.故选:B.【点睛】本题考查了一次函数的应用,解题的关键是读懂图象信息,灵活应用速度、路程、时间之间的关系解决问题.5、B【解析】【分析】根据函数图象可知,小豪出发10分钟后,爸爸追上了小豪,根据此时爸爸的5分钟的行程等于小豪前5分钟的行程与后5分钟的行程和,得到出爸爸的速度与小豪骑自行车的速度的关系,设小豪的速度为x米/分,根据点(,0)列方程可得小豪与爸爸的速度,进而得出爸爸到达公司时,小豪距离书店路程.【详解】解:设小豪骑自行车的速度为xm/min,则爸爸的速度为:(5x+5×x)÷5=x(m/min),∵公司位于家正西方500米,∴(−10−2)×x=500+(5+2.5)x,解得x=200,∴小豪骑自行车的速度为200m/min,爸爸的速度为:200×=300m/min,爸爸到达公司时,丁丁距离商店路程为:3500-(−12)×(300+200)=m.综上,正确的选项为B.故选:B.【点睛】本题考查了一次函数的应用,学会正确利用图象信息,把问题转化为方程解决是本题的关键,属于中考常考题型.6、A【解析】【分析】根据一次函数的增减性分析,即可得到答案.【详解】∵直线上,y随着x的增大而减小又∵ ∴ 故选:A.【点睛】本题考查了一次函数的增减性;解题的关键是熟练掌握一次函数图像的性质,从而完成求解.7、A【解析】略8、C【解析】【分析】根据函数图象中的数据,可以分别计算出两人的速度,从而可以判断各个选项中的说法是否正确,从而可以解答本题.【详解】解:由图象可知,两人出发1小时后相遇,故选项A正确;王明跑步的速度为24÷3=8(km/h),故选项B正确;陈启浩的速度为:24÷1-8=16(km/h),陈启浩从开始到到达目的地用的时间为:24÷16=1.5(h),故陈启浩到达目的地时两人相距8×1.5=12(km),故选项C错误;陈启浩比王提前3-1.5=1.5h到目的地,故选项D正确;故选:C.【点睛】本题考查一次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答.9、D【解析】【分析】根据正比例函数的定义逐个判断即可.【详解】解:A.是二次函数,不是正比例函数,故本选项不符合题意;B.是一次函数,但不是正比例函数,故本选项不符合题意;C.是反比例函数,不是正比例函数,故本选项不符合题意;D.是正比例函数,故本选项符合题意;故选:D.【点睛】本题考查了正比例函数的定义,能熟记正比例函数的定义是解此题的关键,注意:形如y=kx+b(k、b为常数,k≠0)的函数,叫一次函数,当b=0时,函数也叫正比例函数.10、A【解析】【分析】根据一次函数y=3x+a的一次项系数k>0时,函数值随自变量的增大而增大的性质来求解即可.【详解】解:∵一次函数y=3x+a的一次项系数为3>0,∴y随x的增大而增大,∵点(﹣1,y1),(4,y2)在一次函数y=3x+a的图象上,﹣1<4,∴y1<y2,故选:A.【点睛】本题考查了一次函数的性质,掌握,时,随的增大而增大是解题的关键.二、填空题1、>【解析】【分析】由M(1,a)和N(2,b)是一次函数y=-x+1图象上的两点,利用一次函数图象上点的坐标特征可求出a,b的值,比较后即可得出结论.【详解】解:当x=1时,a=-1+1=0;当x=2时,b=-2+1=-1.∵0>-1,∴a>b.故答案为:>.【点睛】本题考查了一次函数图象上点的坐标特征,牢记直线上任意一点的坐标都满足函数关系式y=kx+b是解题的关键.2、【解析】【分析】由两个一次函数的图象平行求解 再把(2,3)代入函数的解析式求解即可.【详解】解: 直线y=kx+b(k≠0)的图像与直线y=-2x平行, 把点(2,3)代入中, 解得: 所以一次函数的解析式为: 故答案为:【点睛】本题考查的是利用待定系数法求解二次函数的解析式,掌握“两直线平行,两个一次函数的比例系数相等,而不相等”是解本题的关键.3、 上升 增大 一、二、三 一、三、四 下降 减小 一、二、四 二、三、四【解析】略4、x≥1【解析】【分析】结合图象,写出直线y=mx+n在直线y=kx+b下方所对应的自变量的范围即可.【详解】解:∵函数y=mx+n的图象与y=kx+b的图象交于点P(1,2),∴当x≥1时,kx+b≥mx+n,∴不等式的解集为x≥1.故答案为:x≥1.【点睛】本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.5、 上升 下降 增大 减小【解析】略三、解答题1、 (1)钢笔的单价为元,笔记本的单价为元.(2)①;②6支或10支【解析】【分析】(1)设钢笔的单价为元,笔记本的单价为元,再根据买10支钢笔和2本笔记本,需230元;买8支钢笔和4本笔记本,需220元,列方程组,再解方程组即可;(2)①当时,由总费用等于购买钢笔与笔记本的费用之和可列函数关系式,②分两种情况列方程,当或 再解方程可得答案.(1)解:设钢笔的单价为元,笔记本的单价为元,则 解得: 答:钢笔的单价为元,笔记本的单价为元.(2)解:①当时,w与a之间的函数关系式为: 所以w与a之间的函数关系式为 ②当时,则 解得: 当时, 解得: 所以李老师购买纪念品一共花了210元钱,他可能购买了6支或支钢笔.【点睛】本题考查的是二元一次方程组的应用,一次函数的应用,掌握“确定相等关系列二元一次方程组与一次函数的关系式”是解本题的关键.2、 (1)y1=﹣x+3(2)n=a+b(3)当a>b时,x>1;当a<b时,x<1【解析】【分析】(1)把(1,2)、(2,b-a-3)分别代入y1=ax+b得到a、b的方程组,然后解方程组得到y1的函数表达式;(2)把A(m,n)分别代入y1=ax+b和y2=bx+a中得到,先利用加减消元法求出m,然后得到n与a、b的关系式;(3)先用a、b表示y3和y4,利用y3>y4得到(a-b)x+b-a>(b-a)x+a-b,然后解不等式即可.(1)解:把(1,2)、(2,b﹣a﹣3)分别代入y1=ax+b得,解得,∴y1的函数表达式为y1=﹣x+3;(2)解:∵y1与y2的图象交于点A(m,n),∴,∴m=1,n=a+b;(3)解:y3=y1﹣y2=ax+b﹣(bx+a)=(a﹣b)x+b﹣a,y4=y2﹣y1=bx+a﹣(ax+b)=(b﹣a)x+a﹣b,∵y3>y4,∴(a﹣b)x+b﹣a>(b﹣a)x+a﹣b,整理得(a﹣b)x>a﹣b,当a>b时,x>1;当a<b时,x<1.【点睛】本题考查了待定系数法求一次函数解析式:设一次函数解析式为y=kx+b(k≠0),再把两组对应量代入,然后解关于k,b的二元一次方程组.从而得到一次函数解析式.也考查了一次函数的性质.3、 (1)s=t;0≤t≤6(2)见解析(3)2【解析】【分析】(1)设直线的解析式为,将代入即可求出,由图象可直接得出的范围;(2)根据甲的速度,可得出行驶时间,得到终点时点的坐标,作出直线即可;(3)用甲行驶的路程减去乙行驶的路程即可.(1)解:设直线的解析式为,且,,解得;;由图象可知,;故答案为:;;(2)解:甲的速度是每小时4千米,甲所用的时间(小时),,图象如下图所示:(3)解:下午3点时,甲、乙两人之间的距离为:.故答案为:2.【点睛】本题考查一次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.4、 (1)一次函数的表达式为;(2)点在直线AB上,见解析【解析】【分析】(1)把(-1,-1)、(1,3)分别代入y=kx+b得到关于k、b的方程组,然后解方程求出k与b的值,从而得到一次函数解析式;(2)先计算出自变量为−3时的函数值,然后根据一次函数图象上点的坐标特征进行判断.(1)解:将和代入,得,解得,,∴一次函数的表达式为(2)解:点C在直线AB上,理由:当时,,∴点在直线AB上.【点睛】本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b,将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;解方程或方程组,求出待定系数的值,进而写出函数解析式.也考查了一次函数图象上点的坐标特征.5、 (1)甲种奖品的单价为20元/件,乙种奖品的单价为10元/件;(2)当学习购买20件甲种奖品、40件乙种奖品时,总费用最少,最少费用是800元.【解析】【分析】(1)设甲种奖品的单价为x元/件,乙种奖品的单价为y元/件,根据“购买1件甲种奖品和2件乙种奖品共需40元,购买2件甲种奖品和3件乙种奖品共需70元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;(2)设购买甲种奖品m件,则购买乙种奖品(60-m)件,设购买两种奖品的总费用为w,由甲种奖品的数量不少于乙种奖品数量的一半,可得出关于m的一元一次不等式,解之可得出m的取值范围,再由总价=单价×数量,可得出w关于m的函数关系式,利用一次函数的性质即可解决最值问题.(1)设甲种奖品的单价为x元/件,乙种奖品的单价为y元/件,依题意,得:,解得,答:甲种奖品的单价为20元/件,乙种奖品的单价为10元/件.(2)设购买甲种奖品m件,则购买乙种奖品(60-m)件,设购买两种奖品的总费用为w元,∵甲种奖品的数量不少于乙种奖品数量的一半,∴m≥(60-m),∴m≥20.依题意,得:w=20m+10(60-m)=10m+600,∵10>0,∴w随m值的增大而增大,∴当学校购买20件甲种奖品、40件乙种奖品时,总费用最少,最少费用是800元.【点睛】本题考查了二元一次方程组的应用、一元一次不等式的应用以及一次函数的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,找出w关于m的一次函数关系式.
相关试卷
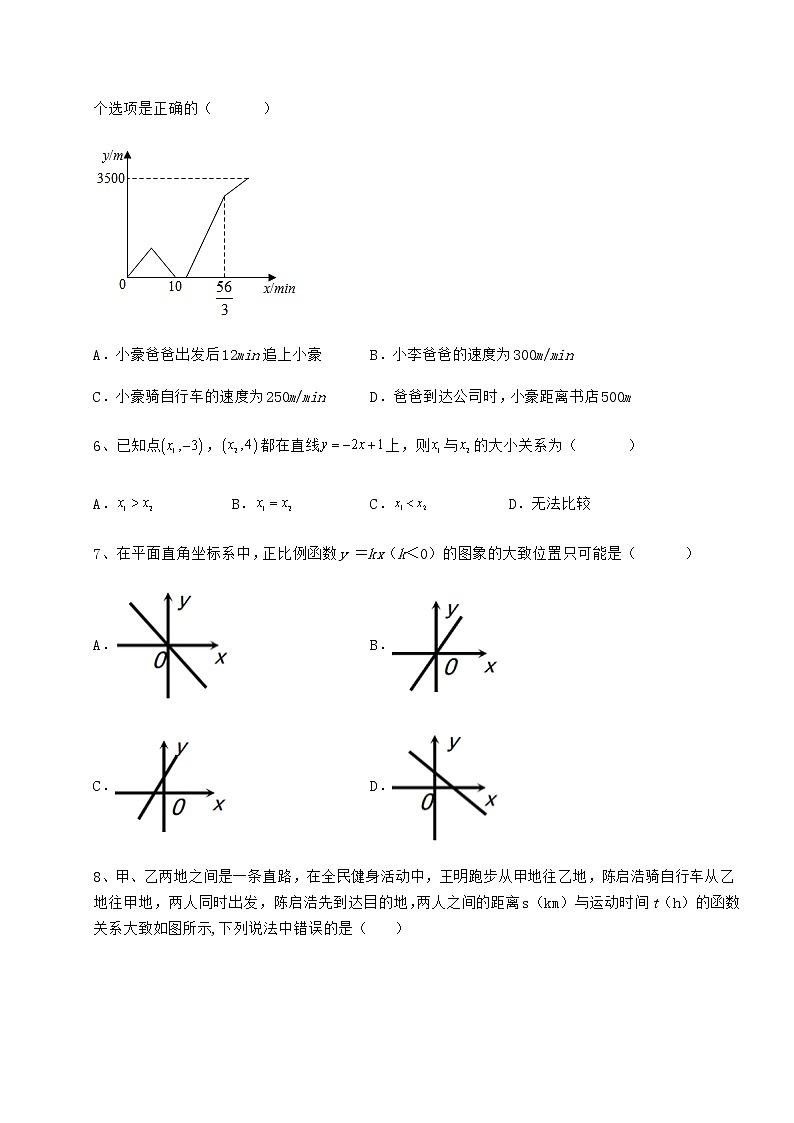
这是一份数学第二十一章 一次函数综合与测试一课一练,共25页。试卷主要包含了直线不经过点等内容,欢迎下载使用。
这是一份初中第二十一章 一次函数综合与测试同步练习题,共29页。试卷主要包含了一次函数y=mx﹣n,已知点,都在直线上,则,当时,直线与直线的交点在等内容,欢迎下载使用。
这是一份初中数学冀教版八年级下册第二十一章 一次函数综合与测试课时练习,共28页。试卷主要包含了若实数,直线不经过点等内容,欢迎下载使用。









