数学八年级下册18.2.1 矩形图文ppt课件

这是一份数学八年级下册18.2.1 矩形图文ppt课件，共21页。PPT课件主要包含了导入新课，探究新知，知识归纳，矩形的四个角都是直角，矩形的对角线相等，例题与练习，有两条对称轴，对角线，对称性，平行四边形等内容，欢迎下载使用。
观察下面图形,长方形在生活中无处不在.
长方形跟我们前面学习的平行四边形有什么关系？
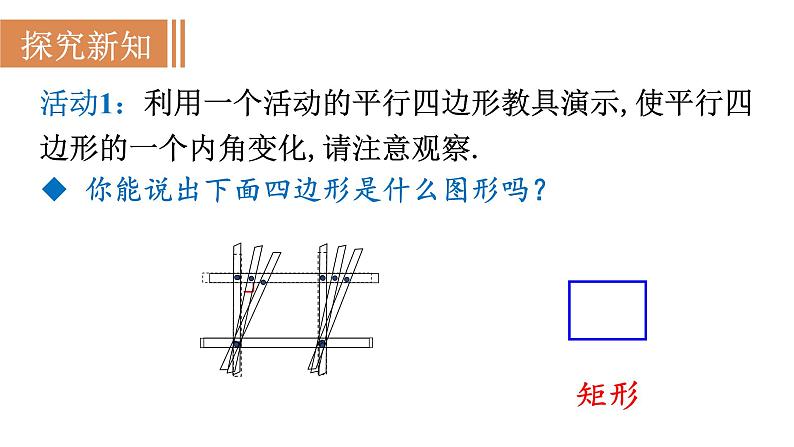
活动1：利用一个活动的平行四边形教具演示,使平行四边形的一个内角变化,请注意观察.
你能说出下面四边形是什么图形吗？
矩形是特殊的平行四边形.
平行四边形不一定是矩形.
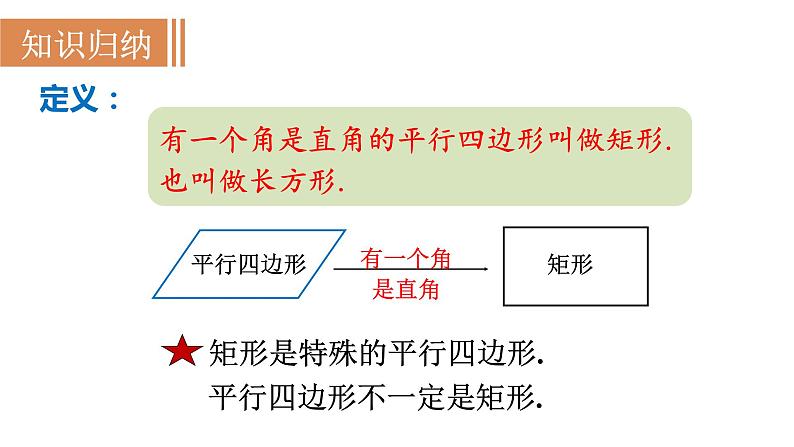
有一个角是直角的平行四边形叫做矩形.也叫做长方形.
矩形是常见的图形，门窗框、书桌面、教科书封面、地砖等都有矩形的形象。
因为矩形是平行四边形，所以它具有平行四边形的所有性质．由于它有一个角为直角，它是否具有一般平行四边形不具有的一些性质呢？
猜想1：矩形的四个角都是直角．
猜想2：矩形的对角线相等．
命题1：矩形的四个角都是直角．
已知：如图，四边形ABCD是矩形
求证：∠A=∠B=∠C=∠D=90°.
证明： ∵四边形ABCD是矩形，
又 矩形ABCD是平行四边形，
∴ ∠A=∠C ， ∠B = ∠D，∠A +∠B = 180°.
∴ ∠A=∠B=∠C=∠D=90°.即矩形的四个角都是直角.
已知：如图，四边形ABCD是矩形，
证明：在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC ， BC = CB.
∴△ABC≌△DCB(SAS).
∴AC = BD，即矩形的对角线相等.
命题2:矩形的对角线相等
求证：AC = BD.
矩形除了具有平行四边形所有性质，还具有的性质有：
在矩形ABCD中，对角线AC与DB相交于点O.
∠ABC=∠BCD=∠CDA=∠DAB =90°，AC=DB.
例1　如图，矩形ABCD的两条对角线AC，BD相交于点O，∠AOB=60°，AB=4 ．求矩形对角线的长．
∴AC与BD相等且互相平分，
∴OA=OB=OC=OD，
解：∵四边形ABCD是矩形，
∴OB=OA=AB=4cm
∴ 矩形的对角线长 AC=BD=2OA=8.
矩形的对角线相等且互相平分
活动：如图，一张矩形纸片，画出两条对角线，沿着对角线AC剪去一半.
问题 Rt△ABC中，BO是一条怎样的线段？它的长度与斜边AC有什么关系？
猜想：直角三角形斜边上的中线等于斜边的一半.
证明: 延长BO至D, 使OD=BO,连接AD、DC.
∵AO=OC, BO=OD，
∴平行四边形ABCD是矩形，
性质：直角三角形斜边上的中线等于斜边的一半.
∴四边形ABCD是平行四边形.
1.矩形是轴对称图形吗？如果是，它有几条对称轴？
解：矩形是轴对称图形；
中心对称图形 轴对称图形
例2　如图，在矩形ABCD中，以顶点B为圆心，边BC长为半径作弧，交AD边于点E，连接BE，CE，过点C作CF⊥BE于点F.求证：BF＝AE.
证明：∵四边形ABCD是矩形，
∴△BFC≌△EAB(AAS)，
∴AD∥BC，∠A＝90°，
∴∠AEB＝∠FBC.
∴∠BFC＝∠A＝90°.
由作图可知BC＝EB.在△BFC和△EAB中，
例3　如图，在△ABC中，AD是高，E，F分别是AB，AC的中点．(1)若AB＝10，AC＝8，求四边形AEDF的周长；
解：∵AD是△ABC的高，E，F分别是AB，AC的中点，
四边形AEDF的周长为AE＋DE＋DF＋AF＝5＋5＋4＋4＝18；
解：∵DE＝AE，DF＝AF，
(2)求证：EF垂直平分AD.
∴E，F在线段AD的垂直平分线上，
当已知条件含有线段的中点、直角三角形的条件时，可联想直角三角形斜边上的中线的性质进行求解．
2．在矩形ABCD中，O是BC的中点，∠AOD＝90°，矩形ABCD的周长为24 cm，则AB的长为(　 　)A．1 cm　　　　　 B．2 cm　　　　　C．2.5 cm　　　　　 D．4 cm
3．如图，在矩形ABCD中，E，F分别是边BC，AB上的点，且EF＝ED，EF⊥ED.求证：AE平分∠BAD.
∴∠B＝∠C＝∠BAD＝90°，
AB＝CD，AD∥BC，
∴∠BEF＋∠BFE＝90°.
∴∠BEF＋∠CED＝90°，
∴∠BFE＝∠CED.
∴△EBF≌△DCE(AAS)，
在△EBF和△DCE中，
∴∠BEA＝∠EAD，
∴∠BAE＝∠BEA.
∴∠BAE＝∠EAD，