数学必修 第一册1.2.3 充分条件、必要条件学案

这是一份数学必修 第一册1.2.3 充分条件、必要条件学案，共8页。

1.2.3　充分条件、必要条件

素养目标·定方向
课程标准
学法解读
1．理解充分条件、必要条件的意义．
2．理解充分不必要、必要不充分和充要条件的意义．
3．掌握充分不必要条件、必要不充分条件和充要条件的判定方法．
4．掌握充分不必要条件、必要不充分条件和充要条件的简单应用.
1．分清命题的条件和结论，正确判断条件与结论之间的推出关系，理解充分条件、必要条件．
2．结合所学的判定定理与性质定理来理解充分条件与必要条件．
3．养成“充要关系”与“集合关系”间的转化意识，就容易判断充要关系或探求充要关系中的参数问题．
4．养成用“逻辑用语”和同学交流的习惯，从而提高交流的严谨性和准确性.

必备知识·探新知

基础知识　　
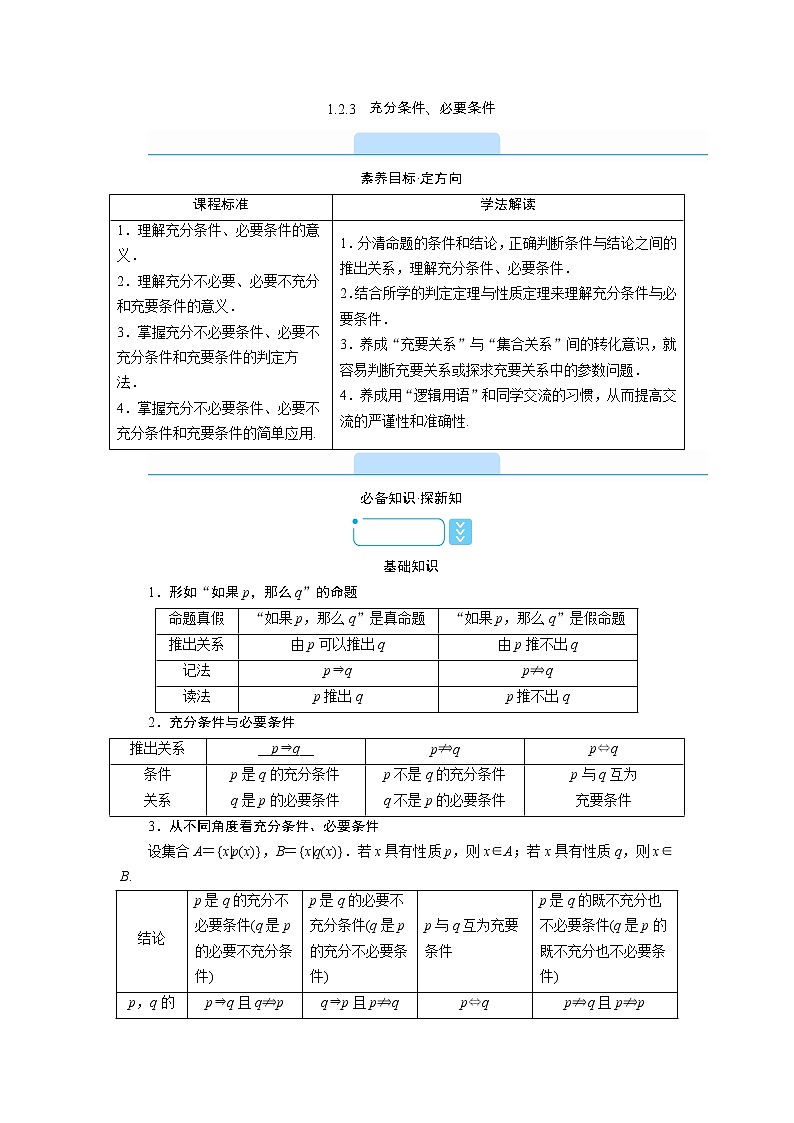
1．形如“如果p，那么q”的命题
命题真假
“如果p，那么q”是真命题
“如果p，那么q”是假命题
推出关系
由p可以推出q
由p推不出q
记法
p⇒q
pq
读法
p推出q
p推不出q
2．充分条件与必要条件
推出关系
__p⇒q__
pq
p⇔q
条件
关系
p是q的充分条件
q是p的必要条件
p不是q的充分条件
q不是p的必要条件
p与q互为
充要条件
3．从不同角度看充分条件、必要条件
设集合A＝{x|p(x)}，B＝{x|q(x)}．若x具有性质p，则x∈A；若x具有性质q，则x∈B.
结论
p是q的充分不必要条件(q是p的必要不充分条件)
p是q的必要不充分条件(q是p的充分不必要条件)
p与q互为充要条件
p是q的既不充分也不必要条件(q是p的既不充分也不必要条件)
p，q的
关系
p⇒q且qp
q⇒p且pq
p⇔q
pq且pp
集合
AB
BA
A＝B
AB且BA




命题
真假
“若p，则q”是真命题，且“若q，则p”是假命题
“若p，则q”是假命题，且“若q，则p”是真命题
“若p，则q”是真命题，且“若q，则p”是真命题
“若p，则q”是假命题，且“若q，则p”是假命题
思考：用定义法判断充分条件和必要条件的一般步骤是什么？
提示：(1)判定“若p，则q”的真假．
(2)尝试从条件推结论，若条件能推出结论，则条件为充分条件，否则就不是充分条件．
(3)尝试从结论推条件，若结论能推出条件，则条件为必要条件，否则就不是必要条件．

基础自测　　
1．“a＋b<0”是“a<0，b<0”的(　C　)
A．充分不必要条件　 B．充要条件
C．必要不充分条件　 D．既不充分也不必要条件
解析：当a与b异号且负数绝对值大时，也有a＋b<0，所以“a＋b<0”“a<0，b<0”，显然“a<0，b<0”⇒“a＋b<0”．所以“a＋b<0”是“a<0，b<0”的必要不充分条件．
2．点P(x，y)是第二象限的点的充要条件是(　B　)
A．x<0，y<0　 B．x<0，y>0
C．x>0，y>0　 D．x>0，y<0
解析：第二象限的点横坐标小于0，纵坐标大于0，所以点P(x，y)是第二象限的点的充要条件是x<0，y>0.
3．命题p：(a＋b)·(a－b)＝0，q：a＝b，则p是q的(　B　)
A．充分条件
B．必要条件
C．既是充分条件也是必要条件
D．既不是充分条件也不是必要条件
解析：由命题p：(a＋b)·(a－b)＝0，得|a|＝|b|，推不出a＝b，由a＝b，能推出|a|＝|b|，故p是q的必要条件．
4．设集合M＝(0,3]，N＝(0,2]，那么“a∈M”是“a∈N”的__必要__条件．
解析：由于NM，所以“a∈N”⇒“a∈M”，所以“a∈M”是“a∈N”的必要条件．
5．已知集合A＝{1，a}，B＝{1,2,3}，则“a＝3”是“A⊆B”的__充分__条件．
解析：因为A＝{1，a}，B＝{1,2,3}，A⊆B，所以a∈B且a≠1，所以a＝2或3，所以“a＝3”是“A⊆B”的充分条件．

关键能力·攻重难
类型　充分条件、必要条件、充要条件的判断
┃┃典例剖析__■
典例1　指出下列各题中p是q的什么条件(在“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”中选一个作答)．
(1)p：x－3＝0，q：(x－2)(x－3)＝0；
(2)p：m－n＝0，m，n∈R，q：＝1，m，n∈R；
(3)p：a>b，q：a＋c>b＋c；
(4)p：a>b，q：ac>bc.
解析：(1)x－3＝0⇒(x－2)(x－3)＝0，但(x－2)(x－3)＝0x－3＝0，故p是q的充分不必要条件．
(2)由＝1得n＝m，即m－n＝0，
反之，当m＝n＝0时，满足m－n＝0，但＝1不成立，
即p是q的必要不充分条件．
(3)a>b⇒a＋c>b＋c，且a＋c>b＋c⇒a>b，故p是q的充要条件．
(4)a>bac>bc，且ac>bca>b，故p是q的既不充分也不必要条件．
典例2　a∈(－∞，－]是方程ax＋3＝0在[－1,2]上有实数根的(　A　)
A．充分不必要条件　 B．必要不充分条件
C．充要条件　 D．既不充分也不必要条件
思路探究：方程ax＋3＝0的实数根是x＝－，解－1≤－≤2要用到分式不等式，这对于我们来说比较难，不妨考虑从“方程ax＋3＝0在[－1,2]上有实数根”的等价形式“直线y＝ax＋3在[－1,2]上与x轴有交点”入手，这样我们得到的都是一次不等式，很容易求出来．
解析：“方程ax＋3＝0在[－1,2]上有实数根”等价于“直线y＝ax＋3在[－1,2]上与x轴有交点”，则
，或解得a≥3或a≤－.
故易得a∈(－∞，－]是方程ax＋3＝0在[－1,2]上有实数根的充分不必要条件．
归纳提升：充分条件、必要条件、充要条件的判断方法
1．定义法
(1)分清哪个是条件，哪个是结论．
(2)判断“如果p，那么q”及“如果q，那么p”的真假．
(3)根据(2)得出结论．
2．集合法：写出集合A＝{x|p(x)}及B＝{x|q(x)}，利用集合间的包含关系进行判断．
3．等价转化法：将命题转化为另一个与之等价的且便于判断真假的命题．
4．特殊值法：对于选择题，可以取一些特殊值或特殊情况，用来说明由条件(结论)不能推出结论(条件)，但是这种方法不适用于证明题．
┃┃对点训练__■
1．用“充分不必要、必要不充分、充要和既不充分也不必要”填空．
(1)是的__充分不必要__条件；
(2)α＝β是＝的__既不充分也不必要__条件；
(3)x＋y≠3是x≠1或y≠2的__充分不必要__条件．
解析：(1)因为结合不等式性质易得反之不成立，如x＝，y＝10，有但不成立，所以是的充分不必要条件．
(2)当α＝β＝0时，，均不存在；
当＝时，取α＝1，β＝－1，但α≠β，所以α＝β是＝的既不充分也不必要条件．
(3)原问题等价于判断“x＝1且y＝2是x＋y＝3的________条件”，故x＋y≠3是x≠1或y≠2的充分不必要条件．
类型　充要条件的证明
┃┃典例剖析__■
典例3　证明：一元二次方程ax2＋bx＋c＝0(a≠0)有一个正根和一个负根的充要条件是ac<0.
思路探究：分清充分性与必要性，理清证明方向．
解析：先证充分性．
由ac<0，可得Δ＝b2－4ac>0，则方程有两个不等实根x1与x2.
由ac<0，可得a，c异号，则x1·x2＝<0，则x1，x2一正一负，即方程ax2＋bx＋c＝0(a≠0)有一个正根和一个负根．
再证必要性．
由方程ax2＋bx＋c＝0(a≠0)的两根x1，x2异号，得x1x2＝<0，则ac<0.
归纳提升：充要条件的证明思路
证明充要条件时要从充分性和必要性两个方面分别证明．
以证明“p成立的充要条件为q”为例．
(1)充分性：把q当作已知条件，结合命题的前提条件，推出p；
(2)必要性：把p当作已知条件，结合命题的前提条件，推出q.
证明的关键是分清哪个是条件，哪个是结论，然后确定推出方向，至于先证明充分性还是先证明必要性则无硬性要求．
┃┃对点训练__■
2．已知关于x的方程ax2＋bx＋c＝0(※)，判断a＋b＋c＝0是否是方程(※)有一个根为1的充要条件．
证明：因为a＋b＋c＝0，
所以c＝－a－b，代入方程ax2＋bx＋c＝0中，得ax2＋bx－a－b＝0，即(x－1)(ax＋a＋b)＝0.
所以方程(※)有一个根为1，所以a＋b＋c＝0⇒方程(※)有一个根为1，
因为方程ax2＋bx＋c＝0有一个根为1，
所以x＝1满足方程ax2＋bx＋c＝0.
所以有a×12＋b×1＋c＝0，即a＋b＋c＝0.
所以方程(※)有一个根为1⇒a＋b＋c＝0，
从而a＋b＋c＝0⇔方程(※)有一个根为1，
因此a＋b＋c＝0是方程(※)有一个根为1的充要条件．
类型　利用充分、必要、充要条件求参数范围
┃┃典例剖析__■
典例4　若p：0 思路探究：→p⇒q，且qp→
解析：由题意得p：0
由题意知p⇒q，qp，则≥3，解得m≥3，即m的取值范围是[3，＋∞)．
归纳提升：根据充分、必要、充要条件求参数的取值范围的步骤
(1)记集合M＝{x|p(x)}，N＝{x|q(x)}．
(2)根据题中条件将问题转化为集合之间的关系：若p是q的充分不必要条件，则MN；若p是q的必要不充分条件，则NM；若p是q的充要条件，则M＝N.
(3)根据集合间的关系列关于参数的不等式(组)．
(4)解不等式(组)即可得参数的取值范围．
┃┃对点训练__■
3．若p：x2＋x－6＝0是q：ax＋1＝0的必要不充分条件，则实数a的值为__－或__.
解析：由x2＋x－6＝0，可得x＝2或x＝－3.
对于ax＋1＝0，当a＝0时，方程无解；
当a≠0时，x＝－.
由题意知pq，q⇒p，则可得a≠0，
此时应有－＝2或－＝－3，
解得a＝－或a＝.
综上可知，a＝－或a＝.
易混易错警示　混淆充分条件与必要条件
┃┃典例剖析__■
典例5　使不等式(2x＋1)(x－3)≥0成立的一个充分不必要条件是(　C　)
A．x≥0　 B．x<0或x>2
C．x∈{－1,3,5}　 D．x≤－或x≥3
错因探究：本题容易颠倒充分性和必要性，认为要在选项中找出{x|x≤－或x≥3}是谁的真子集，从而误选B．事实上，{x|x≤－或x≥3}是结论q，我们要找的是条件p，且条件p满足p⇒q和qp，即要找集合{x|x≤－或x≥3}的真子集．
解析：由(2x＋1)(x－3)≥0得x≤－或x≥3，
选项中只有{－1,3,5}{x|x≤－或x≥3}，
即只有“x∈{－1,3,5}”是“不等式(2x＋1)(x－3)≥0成立”的充分不必要条件．
误区警示：在解答问题时务必看清题干中的问题，明确哪个是条件，哪个是结论，然后根据充分、必要、充要条件的概念进行判断．
学科核心素养　命题成立的充分、必要、充要条件的探求问题
┃┃典例剖析__■
(1)寻求充分、必要条件的思路
①寻求q的充分条件p，即求使q成立的条件p；
②寻求q的必要条件p，即求以q为条件可推出的结论p.
(2)充要条件的探求方法
①探求一个命题成立的充要条件一般有两种处理方法：
方法一：先由结论寻找使之成立的必要条件，再验证它也是使结论成立的充分条件，即保证充分性和必要性都成立．
方法二：变换结论为等价命题，使每一步都可逆，直接得到使命题成立的充要条件．
②求一个命题的充要条件时，往往要从两个方面进行求解，一是充分性，二是必要性．
③在已知充要条件的前提下，充分条件是不确定的，只要保证是充要条件的一个子集即可，而充分不必要条件应为充要条件的一个真子集．
典例6　x∈(0,2)成立的一个必要不充分条件是(　B　)
A．x∈(0,2)　 B．x∈[－1，＋∞)
C．x∈(0,1)　 D．x∈(1,3)
(2)求ax2＋2x＋1＝0至少有一个负实根的充要条件．
思路探究：(1)依题意知本题是寻找一个“选项”，使得该“选项”⇒“题干”，但“题干”“选项”．(2)首先讨论二次项的系数a是否为零，在a≠0时，利用判别式和根与系数的关系求解．
解析：(1)显然选项A为充要条件．因为(0,2)[－1，＋∞)，所以“x∈[－1，＋∞)”是“x∈(0,2)”的一个必要不充分条件．易知C，D均不正确．
(2)由于二次项系数是字母，因此，首先要对方程ax2＋2x＋1＝0判定是一元一次方程还是一元二次方程．
①当a＝0时，为一元一次方程，其根为x＝－，符合要求；
②当a≠0时，为一元二次方程，它有实根的充要条件是判别式Δ≥0即4－4a≥0从而a≤1；
又设方程ax2＋2x＋1＝0的根为x1，x2，则x1＋x2＝－，x1·x2＝.
ⅰ.因为方程ax2＋2x＋1＝0有一个正根、一个负根的充要条件是⇒a<0；
ⅱ.方程ax2＋2x＋1＝0有两个负根的充要条件是⇒0 综上所述，ax2＋2x＋1＝0至少有一个负根的充要条件是a≤1.

课堂检测·固双基
1．“－1 A．充分不必要条件　 B．必要不充分条件
C．充要条件　 D．既不充分也不必要条件
解析：因为(－，3)(－1,6)，所以“－1 2．设a，b是实数，则“a>b”是“a2>b2”的(　D　)
A．充分不必要条件　 B．必要不充分条件
C．充分必要条件　 D．既不充分也不必要条件
解析：“a>b”推不出“a2>b2”，例如，2>－3，但4<9；“a2>b2”也推不出“a>b”，例如，9>4，但－3<2.
3．若“x>a”是“x>2”的充分条件，则实数a的取值范围是__[2，＋∞)__.
解析：由题意得(a，＋∞)⊆(2，＋∞)，所以a≥2.
4．函数y＝kx＋b的图像经过第一、二、三象限的充要条件是__k>0，b>0__.
解析：函数y＝kx＋b的图像经过第一、二、三象限的充要条件是k>0，b>0.
5．已知p：－2≤x≤10，q：1－m≤x≤1＋m(m>0)，若p是q的必要不充分条件，求实数m的取值范围．
解析：p：－2≤x≤10，q：1－m≤x≤1＋m(m>0)．
因为p是q的必要不充分条件，
所以q是p的充分不必要条件，
即[1－m,1＋m][－2,10]，
故有或
解得m≤3.
又m>0，所以实数m的取值范围为(0,3]．