沪科版八年级上册第13章 三角形中的边角关系、命题与证明13.2 命题与证明课堂教学课件ppt

这是一份沪科版八年级上册第13章 三角形中的边角关系、命题与证明13.2 命题与证明课堂教学课件ppt，共10页。PPT课件主要包含了复习提问，真命题，证明的必要性，1什么叫做证明，推理的过程叫做证明，证明的一般步骤，等量代换，对顶角相等，巩固练习等内容，欢迎下载使用。

1、什么叫命题？2、命题由哪两部分组成？3、什么叫做真命题和假命题？
答：1、判断一件事情的语句叫做命题。
2、命题的构成：1)每个命题都是由题设、结论两部分组成.2)命题常写成“如果······那么······”的形式.也可简称为若A则B。
3、命题可分为真命题和假命题：1)真命题：如果题设成立，那么结论一定成立， 像这样的命题叫做真命题。2)假命题：如果题设成立，不能保证结论总是正确，也就是结论不成立，这些命题都是错误的命题，像这样的命题叫做假命题。
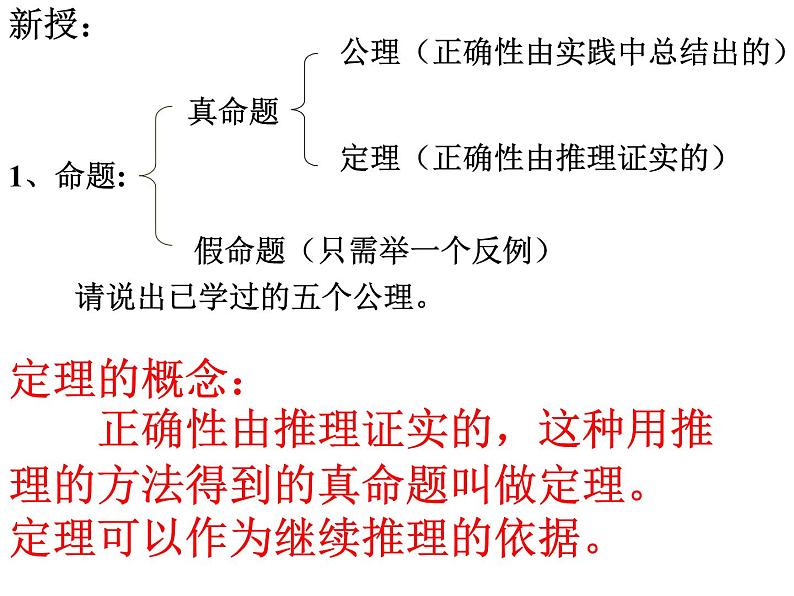
假命题（只需举一个反例）
公理（正确性由实践中总结出的）
定理（正确性由推理证实的）
请说出已学过的五个公理。
直线公理：过两点有且只有一条直线.2) 线段公理：两点之间，线段最短.3) 平行公理：经过直线外一点，有且只有一条 直线与已知直线平行.4) 平行线判定公理：同位角相等，两直线平行.5)平行线性质公理：两直线平行，同位角相等.
定理的概念： 正确性由推理证实的，这种用推理的方法得到的真命题叫做定理。定理可以作为继续推理的依据。
（2）为什么要进行证明？
答：要判断一个命题的真假，必须要有推理论证的过程。只有证明才能区分命题的真假，否则就会得出错误的结论。
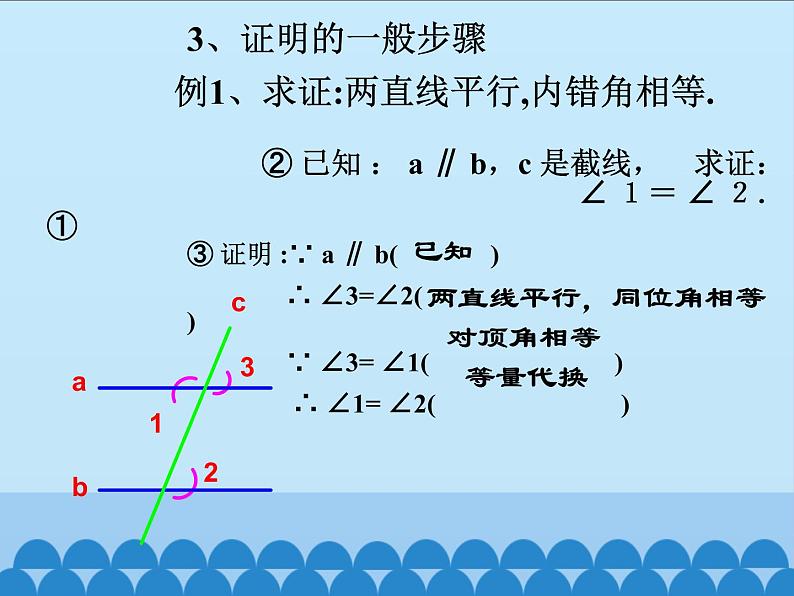
② 已知 ： a ∥ b，c 是截线，　求证： ∠ １＝ ∠ ２．
③ 证明 :∵ a ∥ b(　　　 ) ∴ ∠3=∠2( 　　　 ) ∵ ∠3= ∠1( ) ∴ ∠1= ∠2( )
两直线平行，同位角相等
例1、求证:两直线平行,内错角相等.
小结:证明定理的一般步骤:
1、审题——分清“题设”和“结论”，并画出图形。
2、译题——结合图形中的字母符号写出已知（题设）、 求证（结论）。
3、想题——从已知看可知，推向未知。（“综合法”） 从未知看而知，靠拢已知。（“分析法”） 寻找推理的逻辑通路。
4、证题——从已知出发，步步有据，因果分明写出 全部推理的过程。
例2、证明：同角的余角相等。
已知：∠2是∠1的余角， ∠3是∠1的余角，求证： ∠ 2=∠3。
证明：∵∠2与∠ 1互余， ∠ 3 与∠1互余（已知） ∴ ∠ 1+∠2=90° ∠3 +∠1=90 ° （互为余角的定义）∴ ∠ 1+∠2= ∠3+ ∠1 （等量代换）∴ ∠ 2=∠3 （等式性质）
证明：“如果一条直线和两条平行线中的 一条垂直，那么这条直线也和另一条垂直。”
已知:a∥b,c⊥a ,求证:c⊥b .