2020-2021学年第十三章 相交线 平行线综合与测试课后测评

七年级数学第二学期第十三章相交线 平行线专题攻克

 考试时间：90分钟；命题人：数学教研组

考生注意：

1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟

2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上

3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题  30分）

一、单选题（10小题，每小题3分，共计30分）

1、点P是直线外一点，为直线上三点，，则点P到直线的距离是（      ）

A．2cm B．小于2cm C．不大于2cm D．4cm

2、如图，一条公路经过两次转弯后又回到原来的方向，如果第一次的拐角为150°，则第二次的拐角为（　　）

A．40° B．50° C．140° D．150°

3、如果两个角的一边在同一直线上，另一边互相平行，则这两个角（    ）

A．相等 B．互补 C．互余 D．相等或互补

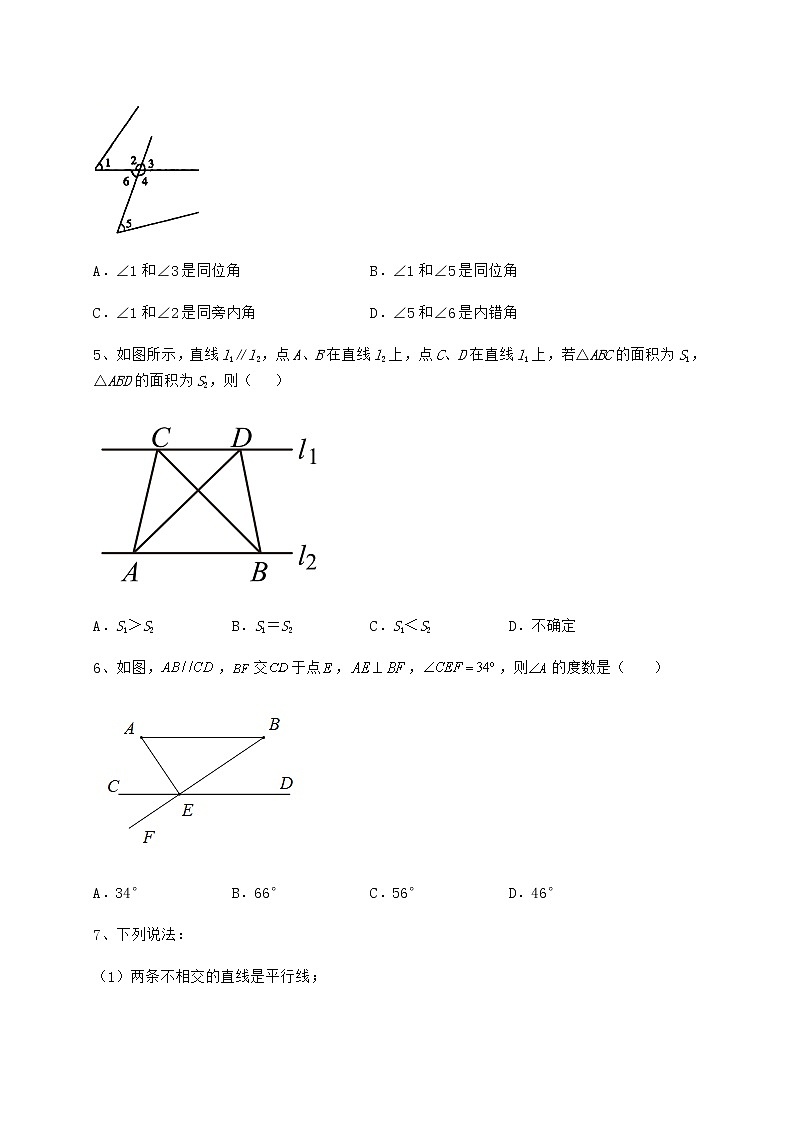
4、如图所示，下列说法错误的是（　　）

A．∠1和∠3是同位角 B．∠1和∠5是同位角

C．∠1和∠2是同旁内角 D．∠5和∠6是内错角

5、如图所示，直线l1∥l2，点A、B在直线l2上，点C、D在直线l1上，若△ABC的面积为S1，△ABD的面积为S2，则（   ）

A．S1＞S2 B．S1＝S2 C．S1＜S2 D．不确定

6、如图，，交于点，，，则的度数是（    ）

A．34° B．66° C．56° D．46°

7、下列说法：

（1）两条不相交的直线是平行线；

（2）过一点有且只有一条直线与已知直线平行；

（3）在同一平面内两条不相交的线段一定平行；

（4）过一点有且只有一条直线与已知直线垂直；

（5）两点之间，直线最短；

其中正确个数是（   ）

A．0个 B．1个 C．2个 D．3个

8、如图，∠1=∠2，∠3=25°，则∠4等于（    ）

A．165° B．155° C．145° D．135°

9、如图，直线，相交于点，，，平分，给出下列结论：①当时，；②为的平分线；③若时，；④．其中正确的结论有（    ）

A．4个 B．3个 C．2个 D．1个

10、如图，在、两地之间要修条笔直的公路，从地测得公路走向是北偏东，，两地同时开工，若干天后公路准确接通，若公路长千米，另一条公路长是千米，且从地测得公路的走向是北偏西，则地到公路的距离是（    ）

A．千米 B．千米 C．千米 D．千米

第Ⅱ卷（非选择题  70分）

二、填空题（5小题，每小题4分，共计20分）

1、下列命题：①等角的余角相等；②过一点有且只有一条直线与已知直线平行；③相等的角是对顶角；④同位角相等；⑤过直线外一点作这条直线的垂线段，则这条垂线段叫做这个点到这条直线的距离．叙述正确的序号是________．

2、如图所示，点A，B，C，D在同一条直线上．在线段PA，PB，PC，PD中，最短的线段是________，理由是________．

3、如图，直线a，b被直线c所截，a∥b，∠1＝60°，则∠2的度数为________．

4、将含30°角的三角板如图摆放，ABCD，若＝20°，则的度数是______．

5、如图，已知，且∠1=48°，则∠2＝_____，∠3＝_____，∠4＝_____．

三、解答题（10小题，每小题5分，共计50分）

1、如图，OB⊥OD，OC平分∠AOD，∠BOC＝35°，求∠AOD和∠AOB的大小．

2、如图，已知AEBF，AC⊥AE，BD⊥BF，AC与BD平行吗？补全下面的解答过程（理由或数学式）．

解：∵AEBF，

∴∠EAB＝          ．（          ）

∵AC⊥AE，BD⊥BF，

∴∠EAC＝90°，∠FBD＝90°．

∴∠EAC＝∠FBD（          ）

∴∠EAB﹣          ＝∠FBG﹣          ，

即∠1＝∠2．

∴                    （          ）．

3、按下面的要求画图，并回答问题：

（1）如图①，点M从点O出发向正东方向移动4个格，再向正北方向移动3个格．画出线段OM，此时M点在点O的北偏东 　   　°方向上（精确到1°），O、M两点的距离是 　   　cm．

（2）根据以下语句，在“图②”上边的空白处画出图形．

画4cm长的线段AB，点P是直纸AB外一点，过点P画直线AB的垂线PD，垂足为点D．你测得点P到AB的距离是 　   　cm．

4、如图，己知AB∥DC，AC⊥BC，AC平分∠DAB，∠B＝50°，求∠D的大小．

阅读下面的解答过程，并填括号里的空白（理由或数学式）．

解：∵AB∥DC（ 　   　），

∴∠B+∠DCB＝180°（ 　   　）．

∵∠B＝（ 　   　）（已知），

∴∠DCB＝180°﹣∠B＝180°﹣50°＝130°．

∵AC⊥BC（已知），

∴∠ACB＝（ 　   　）（垂直的定义）．

∴∠2＝（ 　   　）．

∵AB∥DC（已知），

∴∠1＝（ 　   　）（ 　   　）．

∵AC平分∠DAB（已知），

∴∠DAB＝2∠1＝（ 　   　）（角平分线的定义）．

∵AB∥DC（己知），

∴（ 　   　）+∠DAB＝180°（两条直线平行，同旁内角互补）．

∴∠D＝180°﹣∠DAB＝　   　．

5、补全下列推理过程：已知：如图，CE平分∠BCD，∠1＝∠2＝70°，∠3＝40°，求证：AB∥CD．

证明：∵CE平分∠BCD（______）

∴∠1＝_____（_______）

∵∠1＝∠2＝70°（已知）

∴∠1＝∠2＝∠4＝70°（________）

∴AD∥BC（________）

∴∠D＝180°－_______＝180°－∠1－∠4＝40°

∵∠3＝40°（已知）

∴______＝∠3

∴AB∥CD（_______）

6、如果把图看成是直线AB，EF被直线CD所截，那么

（1）∠1与∠2是一对什么角？

（2）∠3与∠4呢？∠2与∠4呢？

7、如图，点A、B、C在8×5网格的格点上，每小方格是边长为1个单位长度的正方形．请按要求画图，并回答问题：

（1）延长线段AB到点D，使BD＝AB；

（2）过点C画CE⊥AB，垂足为E；

（3）点C到直线AB的距离是 　   　个单位长度；

（4）通过测量 　   　＝　   　，并由此结论可猜想直线BC与AF的位置关系是 　   　．

8、如图，OA⊥OB于点O，∠AOD：∠BOD＝7：2，点D、O、E在同一条直线上，OC平分∠BOE，求∠COD的度数．

9、已知，，三点在同一条直线上，平分，平分．

（1）若，如图1，则      ；

（2）若，如图2，求的度数；

（3）若如图3，求的度数．

10、如图，现有以下3个论断：①ABCD；②∠B＝∠C；③∠E＝∠F．请以其中2个论断为条件，另一个论断为结论构造命题．

（1）你构造的是哪几个命题？

（2）请选择其中一个真命题加以证明．

-参考答案-

一、单选题

1、C

【分析】

根据“直线外一点到直线上各点的所有线段中，垂线段最短”进行解答．

【详解】

解：∵直线外一点与直线上各点连接的所有线段中，垂线段最短，且，

∴点到直线的距离不大于，

故选：C．

【点睛】

本题考查了垂线段最短的性质，熟记性质是解题的关键．

2、D

【分析】

由于拐弯前、后的两条路平行，可考虑用平行线的性质解答．

【详解】

解：∵拐弯前、后的两条路平行，

∴∠B=∠C=150°（两直线平行，内错角相等）．

故选：D．

【点睛】

本题考查平行线的性质，解答此题的关键是将实际问题转化为几何问题，利用平行线的性质求解．

3、D

【分析】

根据平行线的性质，结合图形解答即可．

【详解】

如图，当AE∥BD时，∠EAB与∠DBC符合题意，

∴∠EAB=∠DBC；

如图，当AE∥BD时，∠EAF与∠DBC符合题意，

∵∠EAB+∠EAF=180°，∠EAB=∠DBC，

∴∠DBC +∠EAF=180°，

故选D．

【点睛】

本题考查了平行线的性质，熟练掌握平行线的性质，灵活运用属性结合是解题的关键．

4、B

【分析】

根据同位角、内错角、同旁内角的意义：两条直线被第三条直线所截，在截线的同旁，在被截的两直线的同一侧的角叫做同位角；两条直线被第三条直线所截，两个角分别在截线的两侧，且夹在两条被截直线之间的两个角叫做内错角；两条直线被第三条直线所截，在截线同旁，且在被截两条直线之内的两角叫做同旁内角，可得答案．

【详解】

解：A、∠1和∠3是同位角，故此选项不符合题意；

 B、∠1和∠5不存在直接联系，故此选项符合题意；

 C、∠1和∠2是同旁内角，故此选项不符合题意；

 D、∠1和∠6是内错角，故此选项不符合题意；

故选B．

【点睛】

本题考查了同位角、内错角、用旁内角，利用同位角、内错角、同旁内角的意义是解题关键．

5、B

【分析】

由题意根据两平行线间的距离处处相等，可知△ABC和△ABD等底等高，结合三角形的面积公式从而进行分析即可．

【详解】

解：因为l1∥l2，所以C、D两点到l2的距离相等，即△ABC和△ABD的高相等．同时△ABC和△ABD有共同的底AB，所以它们的面积相等．

故选：B.

【点睛】

本题考查平行线间的距离以及三角形的面积，解题时注意等高等底的两个三角形的面积相等．

6、C

【分析】

由余角的定义得出的度数，由两直线平行内错角相等即可得出结论．

【详解】

解：∵，，

∴，

∵，

∴，

故选：C

【点睛】

本题考查了平行线的性质和余角，解题的关键是灵活运用所学知识解决问题．

7、B

【分析】

根据平面内相交线和平行线的基本性质逐项分析即可．

【详解】

解：（1）在同一平面内，两条不相交的直线是平行线，故原说法错误；

（2）过直线外一点有且只有一条直线与已知直线平行，故原说法错误；

（3）在同一平面内两条不相交的线段不一定平行，故原说法错误；

（4）过一点有且只有一条直线与已知直线垂直，故原说法正确；

（5）两点之间，线段最短，故原说法错误；

故选：B．

【点睛】

本题考查平面内两直线的关系，及其推论等，掌握基本概念和推论是解题关键．

8、B

【分析】

设∠4的补角为，利用∠1=∠2求证，进而得到，最后即可求出∠4．

【详解】

解：设∠4的补角为，如下图所示：

∠1=∠2，

，

，

．

故选：B．

【点睛】

本题主要是考查了平行线的性质与判定，熟练角相等，证明两直线平行，然后利用平行关系证明其他角相等，这是解决该题的关键．

9、B

【分析】

由邻补角，角平分线的定义，余角的性质进行依次判断即可．

【详解】

解：∵∠AOE=90°，∠DOF=90°，

∴∠BOE=90°=∠AOE=∠DOF，

∴∠AOF+∠EOF=90°，∠EOF+∠EOD=90°，∠EOD+∠BOD=90°，

∴∠EOF=∠BOD，∠AOF=∠DOE，

∴当∠AOF=50°时，∠DOE=50°；

故①正确；

∵OB平分∠DOG，

∴∠BOD=∠BOG，

∴∠BOD=∠BOG=∠EOF=∠AOC，

故④正确；

∵，

∴∠BOD=180°-150°=30°，

∴

故③正确；

若为的平分线，则∠DOE=∠DOG，

∴∠BOG+∠BOD=90°-∠EOE，

∴∠EOF=30°，而无法确定，

∴无法说明②的正确性；

故选：B．

【点睛】

本题考查了邻补角，角平分线的定义，余角的性质，数形结合是解决本题的关键．

10、B

【分析】

根据方位角的概念，图中给出的信息，再根据已知转向的角度求解．

【详解】

解：根据两直线平行，内错角相等，可得∠ABG＝48°，

∵∠ABC＝180°−∠ABG−∠EBC＝180°−48°−42°＝90°，

∴AB⊥BC，

∴A地到公路BC的距离是AB＝8千米，

故选B．

【点睛】

此题是方向角问题，结合生活中的实际问题，将解三角形的相关知识有机结合，体现了数学应用于实际生活的思想．

二、填空题

1、①

【分析】

根据相交线与平行线中的一些概念、性质判断，得出结论．

【详解】

①等角的余角相等，故正确；

②中，需要前提条件：过直线外一点，故错误；

③中，相等的角不一定是对顶角，故错误；

④中，仅当两直线平行时，同位角才相等，故错误；

⑤中应为垂线段的长度叫做这个点到这条直线的距离，故错误．

故答案为：①．

【点睛】

本题考查概念、性质的判定，注意，常考错误类型为某一个性质缺少前提条件的情况，因此我们需要格外注意每一个性质的前提条件．解题的关键是熟练掌握以上概念、性质的判定．

2、PC    垂线段最短   

【分析】

根据垂线段最短求解即可．

【详解】

解：∵，PA，PB，PD都不垂直于AD，

∴由垂线段最短可得，最短的线段是PC，

理由是：垂线段最短．

故答案为：PC；垂线段最短．

【点睛】

此题考查了垂线段最短的性质，解题的关键是熟练掌握垂线段最短．

3、120°

【分析】

要求∠2的度数，只需根据平行线的性质求得其对顶角的度数．

【详解】

解：∵a∥b，∠1＝60°，

∴∠3＝120°，

∴∠2＝∠3＝120°．

故答案为：120°

【点睛】

考查了平行线的性质，本题应用的知识点为：两直线平行，同旁内角互补的性质及对顶角相等的性质．

4、50°

【分析】

三角形的外角等于不相邻的两个内角和，同位角相等可得出，从而得到的值．

【详解】

解：如图

故答案为：．

【点睛】

本题考察了三角形的外角，平行线的性质．解题的关键在于角度之间的转化和等量关系．

5、48°    132°    48°   

【分析】

根据两直线平行内错角相等可求出∠2，根据两直线平行，同位角相等可求出∠4，同旁内角互补可求出∠3．

【详解】

解：∵    //，∠1=48°，

∴∠2=∠1=48°，

∵    //，∠1=48°，

∴∠4=∠1=48°，

∵    //，

∴∠3+∠4=180°

∴∠3=180°-∠4=180°-48°=132°

故答案为：48°；132°；48°

【点睛】

此题考查了平行线的性质，熟练掌握平行线的性质是解本题的关键．

三、解答题

1、∠AOD=110°，∠AOB=20°

【分析】

根据OB⊥OD，先可求出∠COD，再根据角平分线的性质求出∠AOD，利用角度的关系即可求出∠AOB．

【详解】

解：∵OB⊥OD

∴∠BOD=90°

∵∠BOC＝35°，

∴∠COD=90°-∠BOC＝55°

∵OC平分∠AOD，

∴∠AOD=2∠COD=110°

∴∠AOB=∠AOD-∠BOD=110°-90°=20°．

【点睛】

此题主要考查角度的求解，解题的关键是熟知角平分线的性质、垂直的定义．

2、∠FBG；两直线平行，同位角相等；等量代换；∠EAC；∠FBD；AC；BD；同位角相等，两直线平行

【分析】

由平行线的性质得∠EAB＝∠FBD+∠2，再证∠1＝∠2，然后由平行线的判定即可得出结论．

【详解】

∵AE∥BF，

∴∠EAB＝∠FBG（两直线平行，同位角相等）．

∵AC⊥AE，BD⊥BF，

∴∠EAC＝90°，∠FBD＝90°．

∴∠EAC＝∠FBD（等量代换），

∴∠EAB﹣∠EAC＝∠FBG﹣∠FBD，

即∠1＝∠2．

∴AC∥BD（同位角相等，两直线平行）．

故答案为：∠FBG；两直线平行，同位角相等；等量代换；∠AEC，∠FBD；AC，BD，同位角相等，两直线平行．

【点睛】

本题考查平行线的判定与性质，掌握平行线的判定与性质是解题的关键．

3、（1）图见解析，53，5；（2）图见解析，3．

【分析】

（1）先根据点的移动得到点，再连接点可得线段，然后测量角的度数和线段的长度即可得；

（2）先画出线段，再根据垂线的尺规作图画出垂线，然后测量的长即可得．

【详解】

解：（1）如图，线段即为所求．

此时点在点的北偏东方向上，、两点的距离是，

故答案为：53，5；

（2）如图，线段和垂线即为所求．

测得点到的距离是，

故答案为：3．

【点睛】

本题考查了测量角的大小、线段的长度、作线段和垂线，熟练掌握尺规作图的方法是解题关键．

4、见解析．

【分析】

先根据平行线的性质可得，从而可得，再根据垂直的定义可得，从而可得，然后根据平行线的性质可得，根据角平分线的定义可得，最后根据平行线的性质即可得．

【详解】

解：∵（已知），

∴（两直线平行，同旁内角互补）．

∵（已知），

∴．

∵（已知），

∴（垂直的定义）．

∴．

∵（已知），

∴（两直线平行，内错角相等）．

∵平分（已知），

∴（角平分线的定义）．

∵（己知），

∴（两条直线平行，同旁内角互补）．

∴．

【点睛】

本题考查了平行线的性质、垂直的定义、角平分线的定义等知识点，熟练掌握平行线的性质是解题关键．

5、见解析

【分析】

由已知CE平分∠BCD可得∠1＝ ∠4，利用等式的性质得出∠1＝∠2＝∠4＝70°，根据直线判定定理得出AD∥BC，利用平角定义求出∠D＝180°－∠BCD即可．

【详解】

证明：∵CE平分∠BCD（    已知    ），

∴∠1＝ ∠4 （ 角平分线定义   ），

∵∠1＝∠2＝70°已知，

∴∠1＝∠2＝∠4＝70°（等量代换），

∴AD∥BC（内错角相等，两直线平行），

∴∠D＝180°－∠BCD＝180°－∠1－∠4＝40°，

∵∠3＝40°已知，

∴ ∠D ＝∠3，

∴AB∥CD（内错角相等，两直线平行）．

故答案为：已知；∠4 ，角平分线定义 ；等量代换；内错角相等，两直线平行；∠BCD；∠D；内错角相等，两直线平行．

【点睛】

本题考查平行线判定，角平分线定义，平角，掌握平行线判定方法，角平分线定义，平角是解题关键．

6、（1）∠1与∠2是一对同位角；（2）∠3与∠4是一对内错角，∠2与∠4是一对同旁内角

【分析】

同位角：两条直线被第三条直线所截，在截线的同旁，被截两直线的同一侧的角，我们把这样的两个角称为同位角；内错角：两条直线被第三条直线所截，两个角分别在截线的两侧，且夹在两条被截直线之间，具有这样位置关系的一对角叫做内错角；同旁内角：两条直线被第三条直线所截，在截线同旁，且在被截直线之间的两角，叫做同旁内角；由以上概念进行判断即可．

【详解】

解：直线AB，EF被直线CD所截，

（1）∠1与∠2是一对同位角；

（2）∠3与∠4是一对内错角，∠2与∠4是一对同旁内角．

【点睛】

本题考查同位角、内错角以及同旁内角的识别，掌握这几种角的基本定义是解题关键．

7、（1）见解析；（2）见解析；（3）2；（4），平行

【分析】

（1）根据网格的特点和题意，延长到，使；

（2）根据网格是正方形，垂线的定义，画出，垂足为，点在线段的延长线上，

（3）点C到直线AB的距离即的长，网格的特点即可数出的长；

（4）根据同位角相等，两直线平行，或内错角相等，两直线平行即可得，即可知测量的角度

【详解】

解：（1）（2）如图所示，

（3）由网格可知

即点C到直线AB的距离是个单位长度

故答案为：2

（4）通过测量，可知

故答案为：，平行

【点睛】

本题考查了画线段，画垂线，平行线的性质与判定，点到直线的距离，掌握以上知识是解题的关键．

8、100°

【分析】

由垂直的定义结合两角的比值可求解∠BOD的度数，即可求得∠BOE的度数，再利用角平分线的定义可求得∠BOC的度数，进而可求解∠COD的度数．

【详解】

解：∵OA⊥OB，

∴∠AOB＝90°，

∵∠AOD：∠BOD＝7：2，

∴∠BOD＝∠AOB＝20°，

∴∠BOE＝180°﹣∠BOD＝160°．

∵OC平分∠BOE，

∴∠BOC＝∠BOE＝80°，

∴∠COD＝∠BOC+∠BOD＝80°+20°＝100°．

【点睛】

本题考查了角度的计算，垂直的定义，角平分线的定义，结合垂直的定义和两角的比值求出∠BOD的度数是解题的关键．

9、（1）90；（2）90°；（3）90°

【分析】

（1）由，，三点在同一条直线上，得出，则，由角平分线定义得出，，即可得出结果；

（2）由，则，同（1）即可得出结果；

（3）易证，同（1）得，，即可得出结果．

【详解】

解：（1），，三点在同一条直线上，

，

，

，

平分，平分，

，，

，

故答案为：90；

（2），

，

同（1）得：，，

；

（3），

，

同（1）得：，，

．

【点睛】

本题考查了角平分线定义、角的计算等知识；熟练掌握角平分线定义是解题的关键．

10、（1）由①②得③，由①③得②，由②③得①；（2）由①②得③，见解析

【分析】

（1）分别以其中2句话为条件，第三句话为结论可写出3个命题；

（2）根据平行线的判定与性质对3个命题分别进行证明，判断它们的真假．

【详解】

（1）由①②得③；由①③得②；由②③得①．

（2）证明：由①②得③；

∵ABCD；

∴∠EAB＝∠C

又∵∠B＝∠C；

∴∠EAB＝∠B

∴CEBF；

∴∠E＝∠F．

【点睛】

本题考查了命题与定理，平行线的判定与性质，掌握平行线的判定定理与性质定理是解题的关键．