数学八年级上册第三章 位置与坐标综合与测试习题ppt课件

这是一份数学八年级上册第三章 位置与坐标综合与测试习题ppt课件，共26页。PPT课件主要包含了答案显示，见习题，答案D，答案A等内容，欢迎下载使用。

1．【2020·菏泽】如图，将△ABC绕点A顺时针旋转角α，得到△ADE，若点E恰好在CB的延长线上，则∠BED等于(　　)A. B. αC．α D．180°－α
【点拨】∵∠ABC＝∠ADE，∠ABC＋∠ABE＝180°，∴∠ABE＋∠ADE＝180°.∴∠BAD＋∠BED＝180°.∵∠BAD＝α，∴∠BED＝180°－α.故选D.
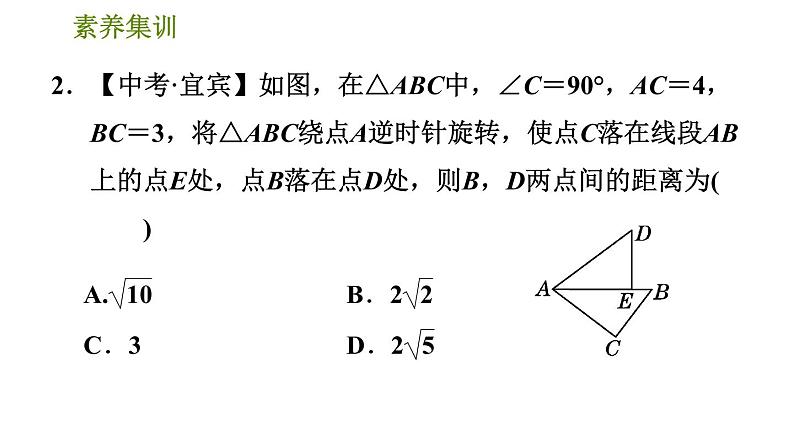
2．【中考·宜宾】如图，在△ABC中，∠C＝90°，AC＝4，BC＝3，将△ABC绕点A逆时针旋转，使点C落在线段AB上的点E处，点B落在点D处，则B，D两点间的距离为(　　)
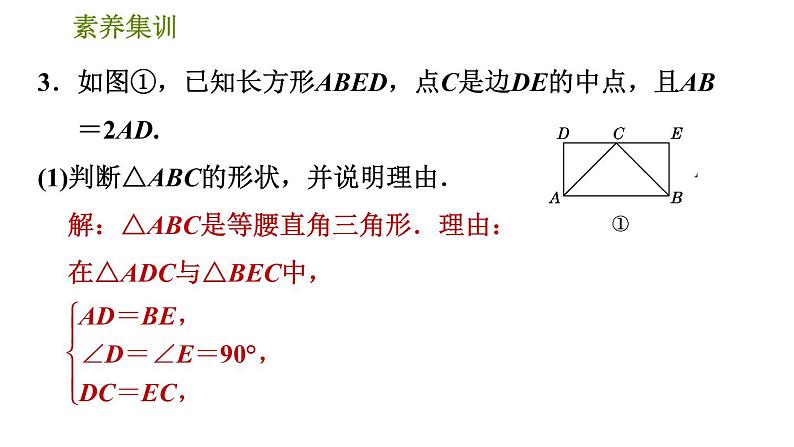
3．如图①，已知长方形ABED，点C是边DE的中点，且AB＝2AD.(1)判断△ABC的形状，并说明理由．
∴△ADC≌△BEC，∴AC＝BC，∠DCA＝∠ECB.∵AB＝2AD＝DE，DC＝CE，∴AD＝DC，∴∠DCA＝45°，∴∠ECB＝45°.∴∠ACB＝180°－∠DCA－∠ECB＝90°.∴△ABC是等腰直角三角形．
(2)保持图①中的△ABC固定不变，绕点C旋转DE所在的直线MN到图②中的位置(垂线段AD，BE在直线MN的同侧)．试探究线段AD，BE，DE的长度之间有什么关系？并给予证明．
解：DE＝AD＋BE.证明：∵∠ACD＋∠CAD＝90°，∠ACD＋∠BCE＝90°，∴∠CAD＝∠BCE.又∵AC＝BC，∠ADC＝∠BEC＝90°，∴△ADC≌△CEB.∴AD＝CE，DC＝EB.∴DC＋CE＝BE＋AD，即DE＝AD＋BE.
(3)保持图②中的△ABC固定不变，继续绕点C旋转DE所在的直线MN到图③中的位置(垂线段AD，BE在直线MN的异侧)．试探究线段AD，BE，DE的长度之间有什么关系？请直接写出结论．
解：DE＝BE－AD.
4．如图，在Rt△ABC中，∠B＝90°，AB＝BC，将一个含30°角的直角三角尺DEF的直角顶点D放在AC的中点上(直角三角尺的短直角边为DE，长直角边为DF)，将直角三角尺DEF绕D点按逆时针方向旋转．(1)如图①，DE交AB于M，DF交BC于N，求证：DM＝DN.
证明：连接BD.∵AB＝BC，∠ABC＝90°，D是斜边AC的中点，
(2)继续旋转至如图②所示的位置，延长AB交DE于点M，延长BC交DF于点N，DM＝DN是否仍然成立？若成立，请给出证明；若不成立，请说明理由．
解：DM＝DN仍然成立．证明如下：连接BD.由(1)知BD⊥AC，BD＝CD，∠ABD＝∠ACB＝45°.∵∠ABD＋∠MBD＝∠ACB＋∠DCN＝180°，∴∠MBD＝∠DCN.∵∠BDM＋∠MDC＝90°＝∠MDC＋∠CDN，∴∠BDM＝∠CDN.又∵BD＝CD，∴△BDM≌△CDN(ASA)． ∴DM＝DN.
5．【中考·日照】如图，在正方形ABCD中，E，F是对角线BD上两点，且∠EAF＝45°，将△ADF绕点A顺时针旋转90°后，得到△ABQ，连接EQ.求证：(1)EA是∠QED的平分线；
证明：∵将△ADF绕点A顺时针旋转90°后，得到△ABQ，∴AQ＝AF，∠BAQ＝∠DAF.∵∠BAD＝90°，∠EAF＝45°，∴∠DAF＋∠BAE＝45°.
证明：∵△AQE≌△AFE，∴QE＝EF.∵将△ADF绕点A顺时针旋转90°后，得到△ABQ，∴QB＝DF，∠ABQ＝∠ADF.易知∠ADF＝∠ABD＝45°，∴∠QBE＝∠ABQ＋∠ABD＝45°＋45°＝90°.∴在Rt△QBE中，QB2＋BE2＝QE2.∴EF2＝BE2＋DF2.
(2)EF2＝BE2＋DF2.
6．【中考·张家界】如图，在正方形ABCD中，AD＝2 ，把边BC绕点B逆时针旋转30°得到线段BP，连接AP并延长交CD于点E，连接PC.求△PCE的面积．
解：∵四边形ABCD是正方形，∴∠ABC＝90°.∵把边BC绕点B逆时针旋转30°得到线段BP，∴PB＝BC＝AB，∠PBC＝30°.∴∠ABP＝60°.∴△ABP是等边三角形．
7．【中考·荆州】在平面直角坐标系中，点A的坐标为(1， )，以原点为中心，将点A顺时针旋转30°得到点A′，则点A′的坐标为(　　)A．( ，1) B．( ，－1)C．(2，1) D．(0，2)
8．【中考·黑龙江】已知：△AOB和△COD均为等腰直角三角形，∠AOB＝∠COD＝90°，连接AD，BC，点H为BC的中点，连接OH.如图①，易证：OH＝ AD且OH⊥AD；将△COD绕点O旋转到图②、图③所示的位置时，线段OH与AD又有怎样的关系？并选择一个图形证明你的结论．