





人教A版 (2019)必修 第一册3.2 函数的基本性质说课ppt课件
展开| 自 学 导 引 |
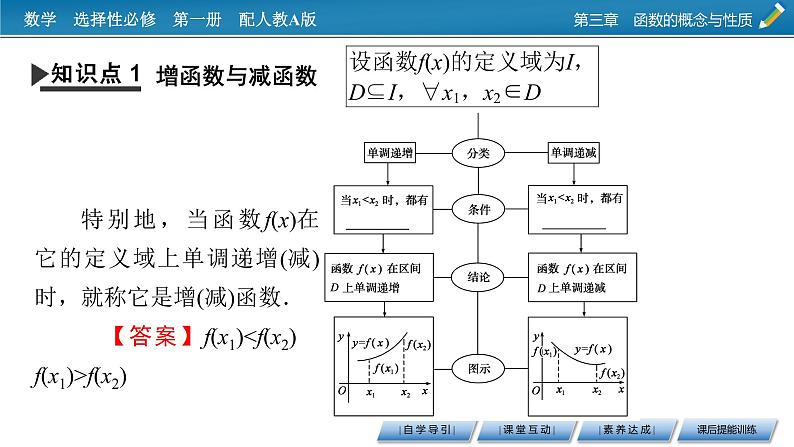
特别地,当函数f(x)在它的定义域上单调递增(减)时,就称它是增(减)函数. 【答案】f(x1)
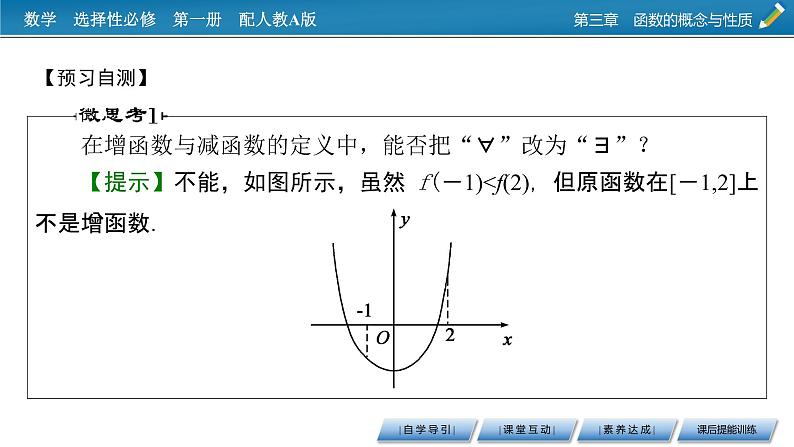
在增函数与减函数的定义中,能否把“∀”改为“∃”?【提示】不能,如图所示,虽然 f(-1)
如果函数y=f(x)在区间D上__________________________,那么就说函数y=f(x)在这一区间具有(严格的)________,区间D叫做y=f(x)的单调区间.
【预习自测】(1)函数f(x)=x2+2x-3的单调减区间是________.(2)函数y=|x|在区间[-2,-1]上( )A.递减 B.递增C.先减后增 D.先增后减【答案】(1)(-∞,-1) (2)A【解析】(1)二次函数f(x)的图象开口向上,对称轴为x=-1,故其单调减区间是(-∞,-1).(2)函数y=|x|的单调减区间是(-∞,0),又[-2,-1]⊆(-∞,0),所以函数y=|x|在区间[-2,-1]上递减.
| 课 堂 互 动 |
(1)如图所示的是定义在区间[-5,5]上的函数y=f(x)的图象,则函数的单调递减区间是________、________,在区间________、________上是单调递增的.
题型1 求函数的单调区间
(2)画出函数y=-x2+2|x|+1的图象并写出函数的单调区间.素养点睛:考查直观想象和逻辑推理的核心素养.【答案】(1)[-2,1] [3,5] [-5,-2] [1,3]
函数的大致图象如图所示,单调增区间为(-∞,-1],[0,1],单调减区间为[-1,0],[1,+∞).
求函数单调区间的2种方法(1)定义法:即先求出定义域,再利用定义法进行判断求解.(2)图象法:即先画出图象,根据图象求单调区间.求函数单调区间的注意点一个函数出现两个或两个以上的单调区间时,不能用“∪”连接两个单调区间,而要用“和”或“,”连接.
素养点睛:考查逻辑推理的核心素养.
题型2 证明函数的单调性
利用定义证明函数单调性的步骤
题型3 用单调性解不等式
已知函数y=f(x)在定义域(-1,1)上单调递减,求满足不等式f(1-a)
已知函数f(x)=x2-2ax-3在区间[1,2]上具有单调性,求实数a的取值范围.素养点睛:考查直观想象和数学运算的核心素养.解:由于二次函数图象的开口向上,对称轴为x=a,故其增区间为[a,+∞),减区间为(-∞,a].而f(x)在区间[1,2]上具有单调性,所以[1,2]⊆[a,+∞)或[1,2]⊆(-∞,a],即a≤1或a≥2.
题型4 根据函数的单调性求参数的取值范围
已知函数的单调性求参数的关注点(1)视参数为已知数,依据基本初等函数的单调性、函数的图象或函数的单调性的定义,确定函数的单调区间,与已知的单调区间比较求参数;(2)分段函数的单调性,除注意各段的单调性外,还要注意衔接点的函数值的大小关系.
已知f(x)是定义在区间[-1,1]上的增函数,且f(x-2)
| 素 养 达 成 |
1.对函数单调性的理解(1)单调性是与“区间”紧密相关的概念,一个函数在定义域不同的区间上可以有不同的单调性.(2)单调性是函数在某一区间上的“整体”性质,因此定义中的x1,x2有以下几个特征:一是任意性,即任意取x1,x2,“任意”二字绝不能丢掉,证明单调性时更不可随意以两个特殊值替换;二是有大小,通常规定x1
1.(题型1)下列函数在区间(0,+∞)上不单调递增的是( )A.y=2x+1B.y=x2+1C.y=3-xD.y=x2+2x+1【答案】C【解析】函数y=3-x在区间(0,+∞)上单调递减.
3.(题型3)函数f(x)是定义域上的单调递减函数,且图象过点(-3,2)和(1,-2),则使|f(x)|<2的x的取值范围是________.【答案】(-3,1)【解析】∵f(x)是定义域上的减函数,f(-3)=2,f(1)=-2,∴当x>-3时,f(x)<2;当x<1时,f(x)>-2.则当-3
人教A版 (2019)必修 第一册2.2 基本不等式背景图课件ppt: 这是一份人教A版 (2019)必修 第一册2.2 基本不等式背景图课件ppt,共42页。PPT课件主要包含了目标认知,上升的,下降的,单调性,单调区间,图3-2-2,图3-2-3等内容,欢迎下载使用。
2020-2021学年3.2 函数的基本性质评课课件ppt: 这是一份2020-2021学年3.2 函数的基本性质评课课件ppt,共44页。PPT课件主要包含了函数的增减性,答案A,答案[1+∞,简记为“同增异减”,01],函数单调性的应用,答案D等内容,欢迎下载使用。
人教A版 (2019)必修 第一册第三章 函数概念与性质3.2 函数的基本性质备课ppt课件: 这是一份人教A版 (2019)必修 第一册第三章 函数概念与性质3.2 函数的基本性质备课ppt课件,共32页。PPT课件主要包含了函数最值的求解,函数最值的应用,答案[12],2恒成立问题,综上可知ga=等内容,欢迎下载使用。













