北师大版 (2019)必修 第二册4.2 平面与平面平行备课ppt课件

这是一份北师大版 (2019)必修 第二册4.2 平面与平面平行备课ppt课件，文件包含第6章42pptx、第6章42DOC等2份课件配套教学资源，其中PPT共44页， 欢迎下载使用。

4.2　平面与平面平行
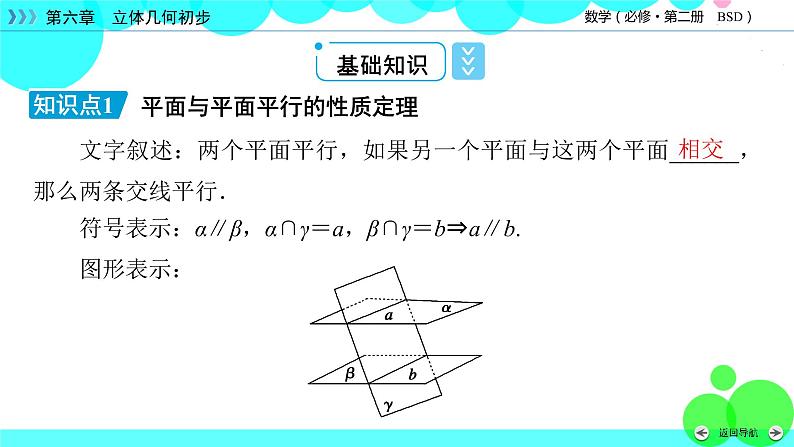
文字叙述：两个平面平行，如果另一个平面与这两个平面______，那么两条交线平行．符号表示：α∥β，α∩γ＝a，β∩γ＝b⇒a∥b.图形表示：
平面与平面平行的性质定理
作用：证明两直线平行．思考1：两个平面平行，一个平面内的直线和另一个平面什么关系呢？提示：平行．
文字叙述：如果一个平面内的两条________与另一个平面平行，那么这两个平面平行．符号表示：a⊂α，b⊂α，a∩b＝A，a∥β，b∥β⇒α∥β.图形表示：
平面与平面平行的判定定理
作用：证明平面与平面平行．思考2：“平面α内存在着不共线的三点到平面β的距离均相等”是“α∥β”的什么条件？提示：不共线的三点有可能不在平面β同一侧，所以应该是“必要不充分”条件．
1．辨析记忆(对的打“√”，错的打“×”)(1)若一个平面内有无数条直线都与另一个平面平行，则这两个平面平行．(　　)(2)若一个平面内任何一条直线都平行于另一个平面，则这两个平面平行．(　　)(3)若α∥β，β∥γ，则α∥γ.(　　)(4)若平面α∥平面β，l⊂平面β，m⊂平面α，则l∥m.(　　)(5)夹在两平行平面间的平行线段相等．(　　)[解析]　(1)这无数条直线相互平行时，这两个平面可能相交．(3)平面的平行具有传递性．(4)这两条直线可能平行也可能异面．
2．若一个平面内的两条直线分别平行于另一个平面内的两条直线，则这两个平面的位置关系是(　　)A．一定平行B．一定相交C．平行或相交D．以上都不对
3．已知直线a，b和平面α，β，则下列结论正确的是(　　)A．若a∥β，α∥β，则a∥αB．若α∥β，a⊂α，则a∥βC．若α∥β，a⊂α，b⊂β，则a∥bD．若a∥β，b∥α，α∥β，则a∥b[解析]　选项A中a可能在α内，选项C中a，b可能异面，选项D中a，b可能异面或相交，选项B中，α∥β，a⊂α，则a与β无公共点，∴a∥β.
4．已知平面α∥平面β，直线l∥α，则(　　)A．l∥βB．l⊂βC．l∥β或l⊂βD．l，β相交[解析]　假设l与β相交，又α∥β，则l与α相交，与l∥α矛盾，则假设不成立，则l∥β或l⊂β.
如图所示，在三棱柱ABC－A1B1C1中，点D，E分别是BC与B1C1的中点．求证：平面A1EB∥平面ADC1．
[分析]　要证平面A1EB∥平面ADC1，只需证平面A1EB内有两条相交直线平行于平面ADC1即可．
[归纳提升]　平面与平面平行的判定方法：(1)定义法：两个平面没有公共点；(2)判定定理：一个平面内的两条相交直线分别平行于另一个平面；(3)转化为线线平行：平面α内的两条相交直线与平面β内的两条相交直线分别平行，则α∥β；(4)利用平行平面的传递性：若α∥β，β∥γ，则α∥γ.
(2021·河南郑州高一检测)如图，两条异面直线AB，CD与三个平行平面α，β，γ分别相交于A，E，B及C，F，D，又AD，BC与平面β的交点为H，G.
求证：四边形EHFG为平行四边形．
[分析]　利用面面平行的性质说明EH∥BD，GF∥BD及EG∥AC，HF∥AC．从而说明四边形EHFG为平行四边形．
【对点练习】❷　 (2020·山东济南联考)如图所示，在三棱锥P－ABC中，D，E，F分别是PA，PB，PC的中点．M是AB上一点，连接MC，N是PM与DE的交点，连接NF，求证：NF∥CM.
　如图所示，两条异面直线BA，DC与两平行平面α，β分别交于B，A和D，C，M，N分别是AB，CD的中点．求证：MN∥平面α.
[归纳提升]　空间中各种平行关系相互转化关系的示意图
【对点练习】❸　如图，在棱长为a的正方体ABCD－A1B1C1D1中，E，F，P，Q分别是BC，C1D1，AD1，BD的中点．(1)求证：PQ∥平面DCC1D1；(2)求PQ的长；(3)求证：EF∥平面BB1D1D．
[解析]　(1)如图所示．
应用定理条件不足，推理论证不严密致误
在长方体ABCD－A1B1C1D1中，E、F、G、H分别是AA1、BB1、CC1、DD1的中点，求证：平面EFGH∥平面ABCD．
1．六棱柱的表面中，互相平行的面最多有(　　)A．2对B．3对C．4对D．5对[解析]　底面为正六边形的六棱柱，互相平行的面最多．
2．下列结论中，错误的是(　　)A．平行于同一直线的两个平面平行B．平行于同一平面的两个平面平行C．平行于同一平面的两直线关系不确定D．两平面平行，一平面内的直线必平行于另一平面
[解析]　如图正方体ABCD－A1B1C1D1中，BB1∥平面ADD1A1，BB1∥平面DCC1D1，而平面ADD1A1∩平面DCC1D1＝DD1．
3．在长方体ABCD－A′B′C′D′中，下列结论正确的是(　　)A．平面ABCD∥平面ABB′A′B．平面ABCD∥平面ADD′A′C．平面ABCD∥平面CDD′C′D．平面ABCD∥平面A′B′C′D′[解析]　由长方体知，平面ABCD∩平面ABB′A′＝AB，所以A不正确；平面ABCD∩平面ADD′A′＝AD，所以B不正确；平面ABCD∩平面CDD′C′＝CD，所以C不正确；平面 ABCD与平面A′B′C′D′是相对平面，两平面平行．
4．已知异面直线l、m，且l∥平面α，m⊂平面α，l⊂平面β，α∩β＝n，则直线m、n的位置关系是______.[解析]　由于l∥平面α，l⊂平面β，α∩β＝n，则l∥n.又直线l、m异面，则直线m、n相交．