




2020-2021学年26.3 实践与探索课文ppt课件
展开我们学习过的函数我们学习过的函数
生活中,我们常会遇到与函数及其图象有关的问题,你会利用所学过的函数解决这些实际问题吗?
26.3 实践与探索26.3 实践与探索
第1课时 实物模型中的判断问题第1课时 实物模型中的判断问题
利用二次函数解决实际问题利用二次函数解决实际问题
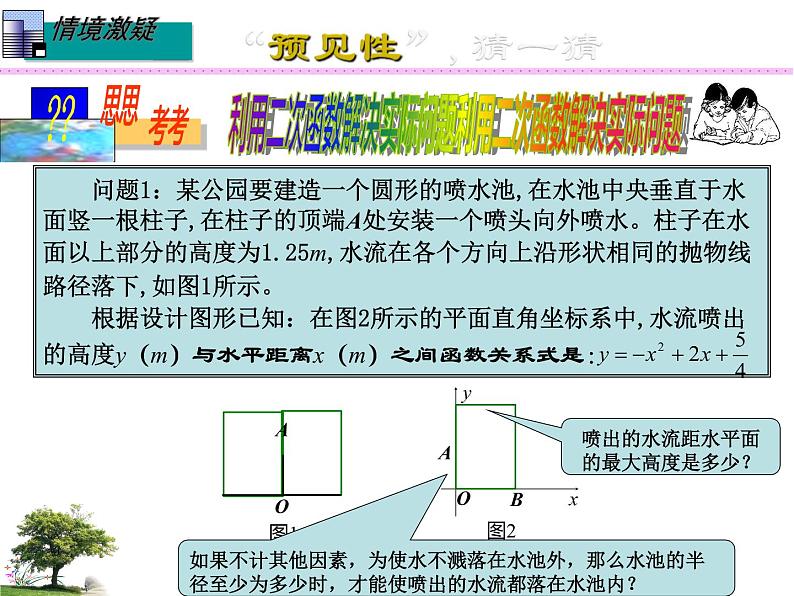
如果不计其他因素,为使水不溅落在水池外,那么水池的半径至少为多少时,才能使喷出的水流都落在水池内?
喷出的水流距水平面的最大高度是多少?
仔细观察,领悟实质仔细观察,领悟实质
求运动路线的最高最远问题求运动路线的最高最远问题
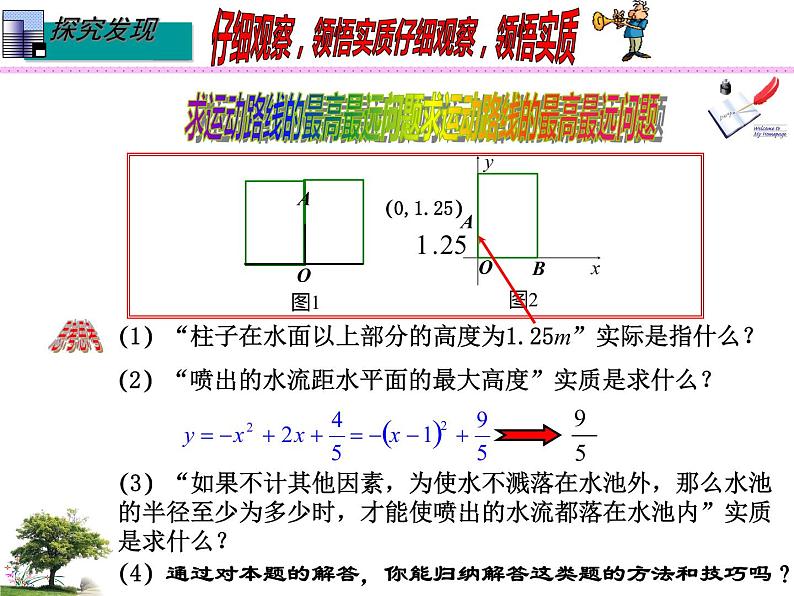
(1)“柱子在水面以上部分的高度为1.25m”实际是指什么?
(2)“喷出的水流距水平面的最大高度”实质是求什么?
(3)“如果不计其他因素,为使水不溅落在水池外,那么水池 的半径至少为多少时,才能使喷出的水流都落在水池内”实质 是求什么?
(4)通过对本题的解答,你能归纳解答这类题的方法和技巧吗?
解决运动路线的最高与最远问题的实质解决运动路线的最高与最远问题的实质
归纳总结,领悟精髓归纳总结,领悟精髓
(Ⅰ)求最高就是求抛物线顶点的纵坐标;
(Ⅱ)求最远就是求抛物线与x轴的交点的横坐标。
物体运动的路线是抛物线形时:
如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
求实物模型的高度和宽度问题求实物模型的高度和宽度问题
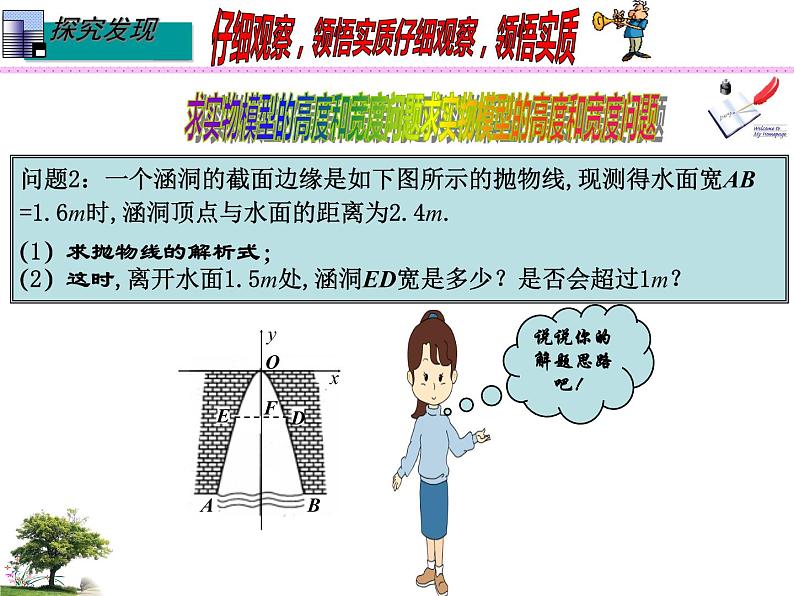
(1)“水面宽AB=1.6m,涵洞顶点与水面的距离为2.4m”实际 是指什么?
(2)如何求抛物线的解析式为好?
(3)“离开水面1.5m处,涵洞宽ED是多少”你是怎样理解的?
解决实物模型的高度和宽度问题解决实物模型的高度和宽度问题
利用二次函数解决抛物线形的隧道、拱门和大桥等实际应用问题:
(Ⅰ)首先要把这些实际问题中的相应数据正确地落实到平面直角 坐标系中的抛物线上,求解得出抛物线所对应的函数表达式;
(Ⅱ)通过二次函数的性质来解决测量问题、最值问题等。
(1)求该抛物线对应的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向 车道,货车从右侧车道通行,那么这辆货车能否安全通过?
(3)在抛物线形拱璧上需要安装两排灯,使它们离地面的高度相等。如 果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
利用二次函数的性质解决实物模型中的判断问题利用二次函数的性质解决实物模型中的判断问题
(1)建立适当的平面直角坐标系;
(2)把实际问题中的数据与点的坐标联系起来;
(3)用待定系数法求出抛物线所对应的函数表达式;
(4)利用二次函数的图像与性质去分析问题。
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
初中数学华师大版九年级下册26.3 实践与探索作业ppt课件: 这是一份初中数学华师大版九年级下册26.3 实践与探索作业ppt课件,共18页。
初中数学26.3 实践与探索精品ppt课件: 这是一份初中数学26.3 实践与探索精品ppt课件,共23页。PPT课件主要包含了复习引入,x≤2,0-6,x-6或x1,x1-4x22,x-4或x2,x-1,合作探究,x2h,方法二等内容,欢迎下载使用。
数学华师大版26.3 实践与探索精品课件ppt: 这是一份数学华师大版26.3 实践与探索精品课件ppt,文件包含263实践与探索2课件pptx、263实践与探索2教案docx等2份课件配套教学资源,其中PPT共28页, 欢迎下载使用。













