初中数学华师大版七年级下册6.3 实践与探索优质课件ppt

这是一份初中数学华师大版七年级下册6.3 实践与探索优质课件ppt，文件包含63实践与探索pptx、63实践与探索导学案docx等2份课件配套教学资源，其中PPT共27页， 欢迎下载使用。

1．列一元一次方程解应用题的步骤是什么？列方程解应用题的步骤：审、设、列、解、答．2．长方形的周长公式、面积公式．C长方形＝2(长＋宽)，S长方形＝长×宽．3．解方程往往并不困难，难的是如何列出方程，列方程最关键的是什么？列方程最关键的是寻找等量关系．
一个关于数学的童话故事
很久很久以前，有一个国王，他有一个非常漂亮的女儿，一年年，漂亮的公主长大了。为了给自己的女儿找到一个好的归宿，国王准备在全国范围内为自己的女儿招亲，因为这是一个农业大国，这个国家的人民非常勤劳。所以，国王要为自己女儿找到一个全国最勤劳最聪明的驸马。
亲爱的子民们： 如果你是20-25岁的年轻小伙子，你拥有勤劳的双手和智慧的头脑，你就有权来参加招亲。 参加招亲的年轻人都将得到一个长100米的栅栏，如果你用这个栅栏围成的长方形耕地种得了所有人中最多的粮食，那么你会成为驸马！
怎样才能围成最大的长方形呢？
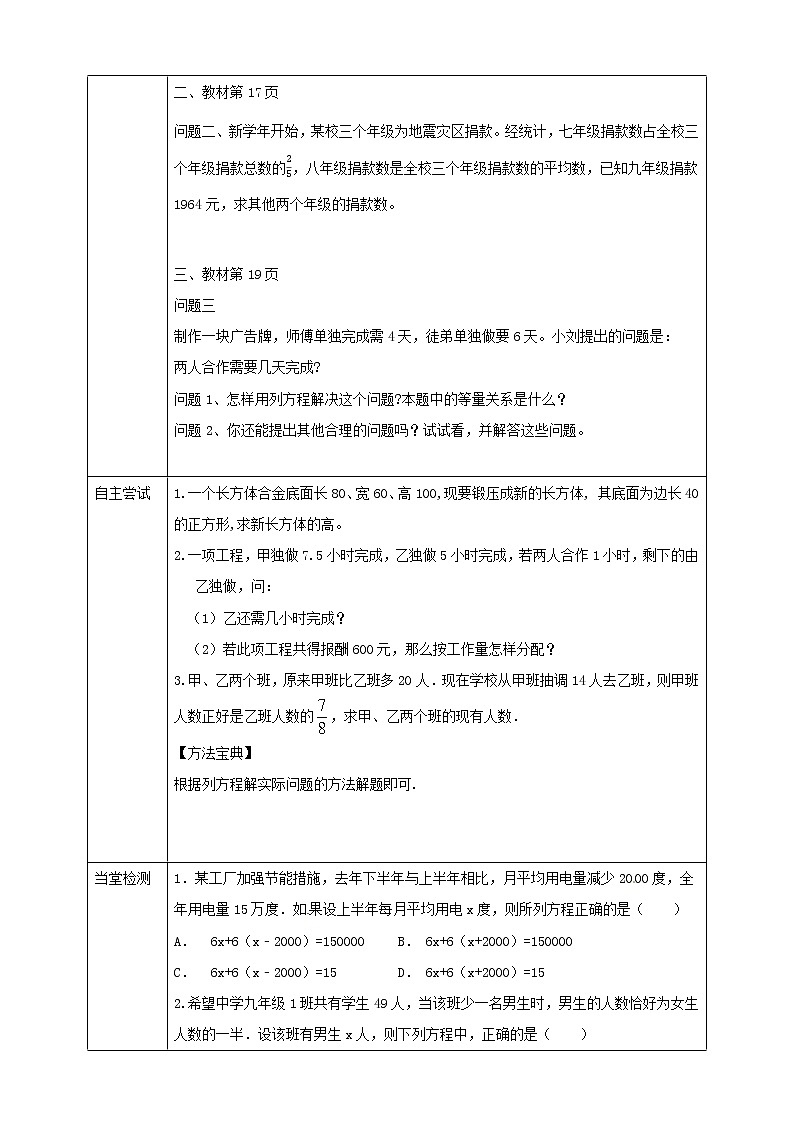
（2）如果长方形的宽比长少4厘米，求这个长方形的面积；
用一根长60厘米的铁丝围成一个长方形，
（3）若设长方形的面积为x平方厘米，能否直接列方程？
(2)解：设长为x，则宽为x-4，由题意得：2(x+x-4)=60 解得：x=17则x-4=17-4=13面积=17×13=221(平方厘米)所以长方形的面积是221平方厘米.
(3)设长方形的面积为x平方厘米，不能找出等量关系， 不能直接列出方程.
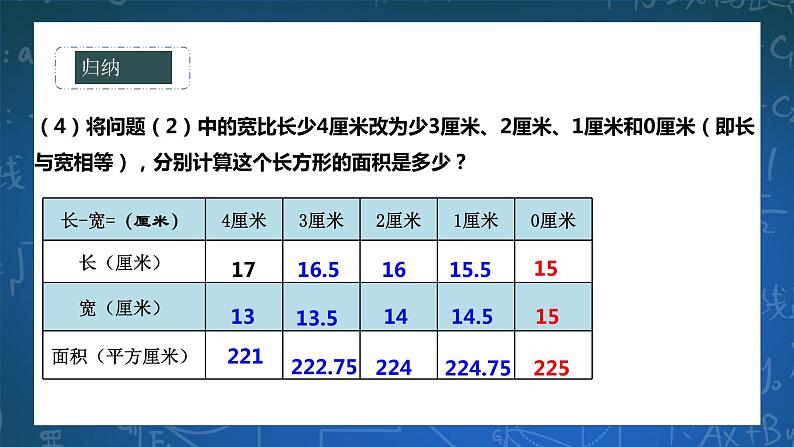
（4）将问题（2）中的宽比长少4厘米改为少3厘米、2厘米、1厘米和0厘米（即长与宽相等），分别计算这个长方形的面积是多少？
注意：长-宽=？也就是长比宽多多少或者宽比长少多少.
观察以上数据，你能发现长方形的面积和长方形的长、宽之差有什么关系么？
长方形在周长一定的条件下，它的长与宽越接近，面积就越大；当长与宽相等，即成为正方形时，面积最大.
实际上，如果两个正数的和不变，当这两个数相等时，它们的积最大，通过以后的学习，我们就会知道其中的道理.
例1. 如图，小明家打算靠墙(墙长14米)修建一个长方形的养鸡场，另三边用35米长的竹篱笆围成，小明的爸爸打算让鸡场的长比宽多2米，小明的妈妈打算让鸡场的长比宽多5米，你认为他们谁的设计合理?按照这种设计，鸡场的面积是多少平方米?
解：设鸡场的宽为x米.
①若按小明爸爸的设计，则其长应为(x+2)米.
x+2+2x=35
因为11+2=13(米)<墙长14米，
所以小明爸爸的设计合理，
这时鸡场的面积为13x11=143(平方米).
②若按小明妈妈的设计，则其长应为(x+5)米.
x+5+2x=35 x=10.
因为10+5=15(米)＞墙长14米，
所以小明妈妈的设计不合理.
周长为80厘米的铁丝，围成一个长方形.
（1）当长方形的长和宽为_______厘米时，面积最大，最大面积是___.
提示：根据上面探究发现的规律，当长和宽相等时，即 长和宽都等于20厘米时，面积最大.
（2）利用上面探究的结果，尝试填空：
若a＞0，b＞0且a+b=3时，ab的最大值为______.
讨论：在解决本题时，你是怎样设元的？还有没有其他的设元方法？比较一下，哪种设元方法比较容易列出方程？说说你的道理.
解得 x=2946∴八年级为2455元.
某市按以下规定收取每月煤气费:如果不超过60立方米，按每立方米0.8元收费；如果超过60立方米，超过部分按每立方米1.2元收费.已知某用户一个月的煤气费平均每立方米0.88元，求该用户这个月应交的煤气费.
解:设该用户这个月所用煤气为x立方米,则根据题意,得：60×0.8+1.2（x-60）=0.88x解得：x=75应缴煤气费0.88x=0.88×75=66答：该用户这个月应交煤气费66元.
1．一件工作，如果甲单独做2小时完成，那么甲独做1小时完成全部工作量的多少?
3．工作量、工作效率、工作时间之间有怎样的关系? 工作效率=工作量÷工作时间
2．一件工作，如果甲单独做x小时完成，那么甲独做1小时，完成全部工作量的多少?
例题1. 制作一块广告牌，师傅单独完成需4天，徒弟单独做要6天.小刘提出的问题是：两人合作需要几天完成?
问题1、怎样用列方程解决这个问题?本题中的等量关系是什么？
问题2、你还能提出其他合理的问题吗？试试看，并解答这些问题.
等量关系：师傅的工作量+徒弟的工作量=1
解：设两人合作需要x天完成.
一项工程,甲队单独完成需40天,乙队单独完成需50天,现甲队单独做4天,后两队合作.(1)求甲、乙合作多少天才能把该工程完成;(2)在(1)的条件下,甲队每天的施工费用为2500元,乙队每天的施工费用为3000元,求完成此项工程需付给甲、乙两队共多少元.
(2)甲队的费用为2500×(20+4)=60000(元),乙队的费用为3000×20=60000(元),60000+60000=120000(元).答:完成此项工程需付给甲、乙两队共120000元.
1．互联网“微商”经营已成为大众创业新途径，某微信平台上一件商品标价为200元，按标价的五折销售，仍可获利20元．设这件商品的进价为x元，则下列方程正确的是(　　)A．x－200×50%＝20 B．200×50%－x＝20C．x－200×(1＋50%)＝20 D．200×(1＋50%)－x＝202．某中学学生郊游，学生沿着与笔直的铁路线并列的公路匀速前进，每小时走4500米，一列火车以每小时120千米的速度迎面开来，测得从车头与队首学生相遇，到车尾与队末学生相遇，共经过60秒，如果队伍长500米，那么火车长为(　　) A．2075米 B．1575米 C．2000米 D．1500米
3. “绿水青山,就是金山银山”.某市开展“保护母亲河”植树造林活动,该市金桥村有1 000亩荒山,绿化率达80%,300亩良田视为已绿化,河坡地植树面积已达20%,目前金桥村所有土地的绿化率为60%,则河坡地有　 　亩.4.某小组几名同学准备到图书馆整理一批图书,若一名同学单独做要40 h完成.现在该小组全体同学一起先做8 h后,有2名同学因故离开,剩下的同学再做4 h,正好完成这项工作.假设每名同学的工作效率相同,问该小组共有多少名同学?若设该小组共有x名同学,根据题意可列方程为　 .  
5.延庆区某中学七年级(1)(2)两个班共104人,要去延庆地质博物馆进行社会大课堂活动,老师指派小明到网上查阅票价信息,小明查得票价如图:
购票张数1～50张每张票的价格为13元
购票张数51～100张 每张票的价格为11元
购票张数100张以上每张票的价格为9元
其中(1)班不足50人,经估算,如果两个班都以班为单位购票,一共应付1240元.
(1)两个班各有多少学生?(2)如果两个班联合起来,作为一个团体购票,可以省多少钱?(3)如果七年级(1)班单独组织去博物馆参观,你认为如何购票最省钱?
解:(1)设七年级(1)班x人,则七年级(2)班(104-x)人,由题意可得13x+11(104-x)=1240,解得x=48,则104-x=56.答:七年级(1)班48人,七年级(2)班56人.(2)1240-104×9=304(元).(3)七年级(1)班按照实际人数购票的费用为48×13=624元,购51张票的费用为51×11=561元.因为624>561,所以购买51张票划算些.