2021年北京石景山区苹果园中学九年级上期末数学试卷

这是一份2021年北京石景山区苹果园中学九年级上期末数学试卷，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共8小题；共40分）
1. 在比例尺是 1:8000 的南京市城区地图上，太平南路的长度约为 25 cm ，它的实际长度约为
A. 320 cmB. 320 mC. 2000 cmD. 2000 m

2. 关于函数 y=−2x2+3，下列说法正确的是
A. 不管 x 取何值，y 总是负数B. 它的图象有最高点
C. 其图象对称轴是直线 x=−1D. y 随 x 的增大而减小

3. 如果 ∠α 是等边三角形的一个内角，那么 csα 的值等于
A. 12B. 22C. 32D. 1

4. 如图，AB 是 ⊙O 的直径，弦 CD 垂直平分 OB，则 ∠BDC= ．
A. 15∘B. 20∘C. 30∘D. 45∘

5. 小莉家附近有一公共汽车站，大约每隔 30 分钟准有一趟车经过.则"小莉在到达该车站后 10 分钟内可坐上车"这一事件的概率是
A. 14B. 13C. 34D. 12

6. 如图，AB 是 ⊙O 的直径，CD 是弦，且 CD⊥AB，BC=6，AC=8，那么 sin∠ABD 的值是
A. 43B. 34C. 35D. 45

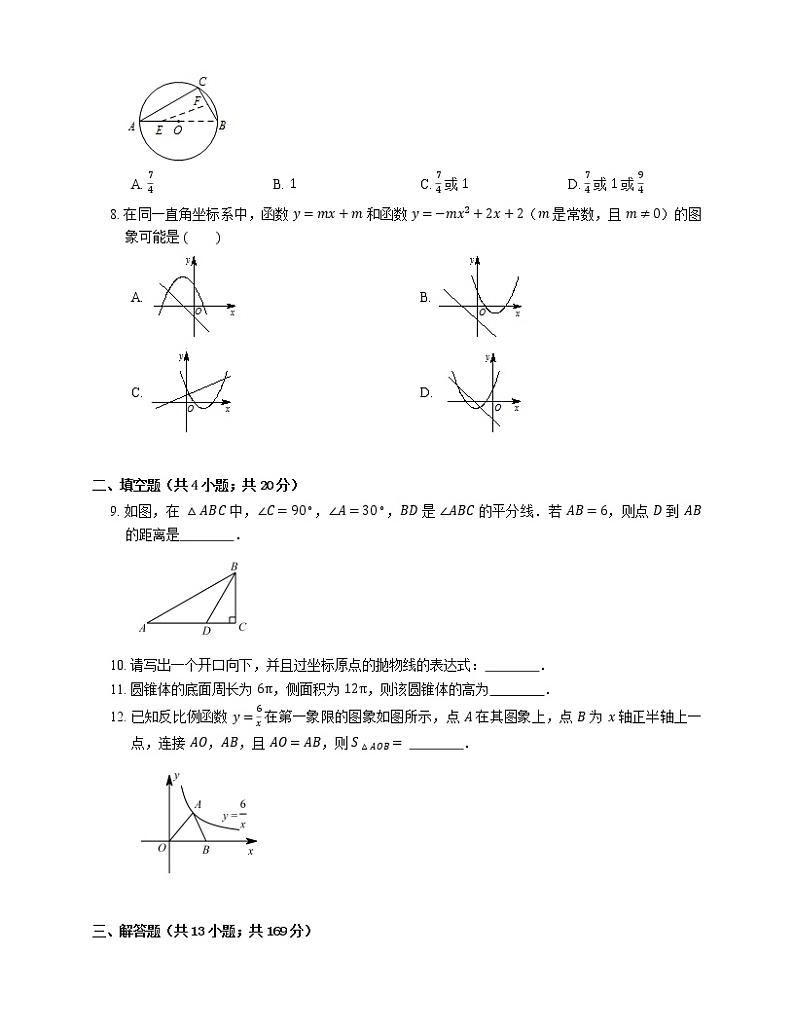
7. 如图，AB 是 ⊙O 的直径，弦 BC=2 cm，F 是弦 BC 的中点，∠ABC=60∘．若动点 E 以 2 cm/s 的速度从 A 点出发沿着 A→B→A 方向运动，设运动时间为 ts0≤t<3，连接 EF，当 △BEF 是直角三角形时，ts 的值为 ．
A. 74B. 1C. 74 或 1D. 74 或 1 或 94

8. 在同一直角坐标系中，函数 y=mx+m 和函数 y=−mx2+2x+2（m 是常数，且 m≠0）的图象可能是
A. B.
C. D.

二、填空题（共4小题；共20分）
9. 如图，在 △ABC 中，∠C=90∘，∠A=30∘，BD 是 ∠ABC 的平分线．若 AB=6，则点 D 到 AB 的距离是 ．

10. 请写出一个开口向下，并且过坐标原点的抛物线的表达式： ．

11. 圆锥体的底面周长为 6π，侧面积为 12π，则该圆锥体的高为 ．

12. 已知反比例函数 y=6x 在第一象限的图象如图所示，点 A 在其图象上，点 B 为 x 轴正半轴上一点，连接 AO，AB，且 AO=AB，则 S△AOB= ．

三、解答题（共13小题；共169分）
13. 计算：4cs30∘−3tan60∘+2sin45∘⋅cs45∘．

14. 如图，CD 是 Rt△ABC 斜边上的高，DE⊥BC 于 E，求证：ACBD=CDBE．

15. 商场为了促销某件商品，设置了如图的一个转盘，它被分成了 3 个相同的扇形．各扇形分别标有数字 2，3，4，指针的位置固定，该商品的价格由顾客自由转动此转盘两次来获取，每次转动后让其自由停止，记下指针所指的数字（指针指向两个扇形的交线时，当作右边的扇形），先记的数字作为价格的十位数字，后记的数字作为价格的个位数字，则顾客购买商品的价格不超过 30 元的概率是多少?

16. 如图，已知反比例函数 y1=k1x（k1>0）与一次函数 y2=k2x+1k2≠0 相交于 A，B 两点，AC⊥x 轴于点 C，若 △OAC 的面积为 1，且 tan∠AOC=2．
（1）求出反比例函数与一次函数的解析式．
（2）请直接写出 B 点的坐标，并指出当 x 为何值时，反比例函数 y1 的值大于一次函数 y2 的值?

17. 如图所示，在一次课外实践活动中，同学们要测量某公园人工湖两侧 A，B 两个凉亭之间的距离，现测得 AC=30 m，BC=70 m，∠CAB=120∘，请计算 A，B 两个凉亭之间的距离．

18. 已知：如图所示，点 D 、 E 分别在等边 △ABC 的边 BC 、 AC 上，且 AE=CD，AD 与 BE 相交于点 F．
（1）求证：△ABE≌△CAD
（2）求 ∠BFD 的度数．

19. 在二次函数 y=ax2+bx+ca≠0 中，函数 y 与自变量 x 的部分对应值如下表：
x⋯−10123⋯y⋯830−10⋯
（1）求这个二次函数的表达式；
（2）当 x 的取值范围满足什么条件时，y<0 ?

20. 如图，A，B，H 是直线 l 上的三个点，AC⊥l 于点 A，BD⊥l 于点 B，且 HC=HD，AB=5，AC=2，BD=3，求 AH 的长．

21. 已知关于 x 的二次函数 y=ax2+bx+c 的图象的对称轴是直线 x=2，图象在 x 轴上截得的线段长为 6，与 y 轴交点的纵坐标为 5，求这个二次函数的解析式．

22. 如图，已知 △PQR 中，∠R=90∘，PR=8，PQ=10．求 tanP，ctP 的值．

23. 在 △AOB 中，C，D 分别是 OA，OB 边上的点，将 △OCD 绕点 O 顺时针旋转到 △OCʹDʹ．
（1）如图 1，若 ∠AOB=90∘，OA=OB，C，D 分别为 OA，OB 的中点，证明：
① ACʹ=BDʹ；
② ACʹ⊥BDʹ；
（2）如图 2，若 △AOB 为任意三角形且 ∠AOB=θ，CD∥AB，ACʹ 与 BDʹ 交于点 E，猜想 ∠AEB=θ 是否成立?请说明理由．

24. 如图，在矩形 ABCD 中，E 、 F 分别是边 AB 、 CD 上的点，AE=CF，连接 EF，BF，EF 与对角线 AC 交于 O 点，且 BE=BF，∠BEF=2∠BAC．
（1）求证：OE=OF；
（2）若 BC=23，求 AB 的长．

25. 抛物线 y=ax2+bx+c，若 a，b，c 满足 b=a+c，则称抛物线 y=ax2+bx+c 为“恒定”抛物线．
（1）求证：“恒定”抛物线 y=ax2+bx+c 必过 x 轴上的一个定点 A；
（2）已知“恒定”抛物线 y=3x2−3 的顶点为 P，与 x 轴另一个交点为 B，是否存在以 Q 为顶点，与 x 轴另一个交点为 C 的“恒定”抛物线，使得以 PA，CQ 为边的四边形是平行四边形?若存在，求出抛物线解析式；若不存在，请说明理由．
答案
第一部分
1. D
2. B
3. A
4. C【解析】
连接 OC．
∵ 弦 CD 垂直平分 OB，
∴OE=12CO，∠COB=60∘，
∴∠BDC=30∘．
5. B
6. D【解析】∵AB 是 ⊙O 的直径，
∴∠ACB=90∘，
根据勾股定理可得 AB=10．
∵CD⊥AB，
∴AD=AC．
∴sin∠ABD=sin∠ABC=ACAB=45．
7. D【解析】①当点 F 为直角顶点时，t=1 s；
②当点 E 为直角顶点时，t=74 s 或 t=94 s．
8. D【解析】结核函数图象：
当 m>0 时，一次函数 y=mx+m 经过一、二、三象限，
此时二次函数 y=−mx2+2x+2 中 −m<0，开口向下，与 y 轴的交点为 0,2，对称轴在 y 轴的右侧，
∴ C选项错误．
当 m<0 时，一次函数 y=mx+m 经过二、三、四象限，
此时二次函数 y=−mx2+2x+2 中 −m>0，开口向上，与 y 轴的交点为 0,2，对称轴在 y 轴的左侧，
先排除A（A选项开口向下），B（对称轴所在位置不对），
∴ 选择D．
第二部分
9. 3
【解析】由已知易得 △ADE≌△BDE≌△BDC．
10. y=−x2+2x（答案不唯一）
【解析】∵ 开口向下，
∴a<0，
∵ 抛物线过坐标原点，
∴c=0，
∴ 答案不唯一，如 y=−x2+2x．
11. 7
【解析】设圆锥的母线长为 R，圆锥的高为 h，圆锥底面圆的半径为 r．
∵ 圆锥体的底面周长为 6π，
∴r=3．
∵ 侧面积为 12π，
∴S侧=12lR，l=6π，
∴R=4，
∴h=R2−r2=42−32=7．
12. 6
【解析】设点 A 的坐标为 a,6a，
∵AO=AB，点 B 在 x 轴上，
∴ 点 B 的坐标为 2a,0．
∴S△AOB=12×2a×6a=6．
第三部分
13. 原式=4×32−3×3+2×22×22=1−3.
14. 由于在直角 △ABC 中，DE⊥BC，AB⊥BC，
所以 DE∥AC，∠A=∠BDE，∠ADC=∠DEB，
所以 △ADC≌△BDE，ACBD=CDBE．
15.
共有 9 种等可能的情况，符合题意的有 3 种，
顾客购买商品的价格不超过 30 元的概率为 13．
16. （1） 在 Rt△OAC 中，设 OC=m，
∵tan∠AOC=ACOC=2，
∴AC=2×OC=2m，
∵S△OAC=12×OC×AC=12×m×2m=1，
∴m2=1，
∴m=±1（负值舍去），
∴A 点的坐标为 1,2，
把 A 点的坐标代入 y1=k1x 中，得 k1=2，
∴ 反比例函数的表达式为 y1=2x，
把 A 点的坐标代入 y2=k2x+1 中，得 k2+1=2，
∴k2=1，
∴ 一次函数的表达式 y2=x+1．
（2） −2,−1，017.
如图所示，过 C 点作 CD⊥AB，垂足为 D．
∵∠CAB=120∘，
∴∠CAD=60∘．
∵cs∠CAD=ADAC，
∴AD=AC⋅cs∠CAD=30×cs60∘=15m，
∴CD=AC2−AD2=302−152=153m，
∴BD=BC2−CD2=702−1532=65m，
∴AB=BD−AD=65−15=50m．
答：A 、 B 两个凉亭之间的距离为 50 m．
18. （1） ∵△ABC 是等边三角形
∴∠BAE=∠C=60∘，AB＝AC .
∵AE=CD，
∴△ABE≌△CAD .
（2） ∵△ABE≌△CAD，
∴∠ABF=∠EAF .
∵∠BFD=∠ABF+∠BAF，
∴∠BFD=∠EAF+∠BAF=∠BAC=60∘ .
19. （1） 依题意，所求抛物线的解析式为 y=ax2+bx+3．
由题意，得 a+b+3=0,4a+2b+3=−1.
解得 a=1,b=−4.
∴ 这个二次函数的解析式是 y=x2−4x+3．
（2） 当 120. 设 AH=xx>0，则 BH=AB−AH=5−x，
∵AC⊥l 于点 A，BD⊥l 于点 B，
∴△ACH 和 △BDH 都是直角三角形，
在 Rt△ACH 中，HC2=AC2+AH2=4+x2，
在 Rt△BDH 中，HD2=BD2+BH2=9+5−x2=34−10x+x2，
∵HC=HD，
∴HC2=HD2，
即 4+x2=34−10x+x2，
解得 x=3，
即 AH 的长为 3．
21. y=−x2+4x+5．
22. tanP=34，ctP=43．
23. （1） ① ∵△OCD 旋转到 △OCʹDʹ，
∴OC=OCʹ，OD=ODʹ，∠AOCʹ=∠BODʹ，
∵OA=OB，C，D 分别为 OA，OB 的中点，
∴OC=OD，
∴OCʹ=ODʹ，
在 △AOCʹ 和 △BODʹ 中，
OA=OB,∠AOCʹ=∠BODʹ,OCʹ=ODʹ,
∴△AOCʹ≌△BODʹ（SAS），
∴ACʹ=BDʹ；
②延长 ACʹ 交 BDʹ 于 E，交 BO 于 F，如图 所示：
∵△AOCʹ≌△BODʹ，
∴∠OACʹ=∠OBDʹ，
又 ∠AFO=∠BFE，∠OACʹ+∠AFO=90∘，
∴∠OBDʹ+∠BFE=90∘，
∴∠BEA=90∘，
∴ACʹ⊥BDʹ．
（2） ∠AEB=θ 成立，
理由如下：如图所示：
∵△OCD 旋转到 △OCʹDʹ，
∴OC=OCʹ，OD=ODʹ，∠AOCʹ=∠BODʹ．
∵CD∥AB，
∴OCOA=ODOB，
∴OCʹOA=ODʹOB，
∴OCʹODʹ=OAOB．
又 ∠AOCʹ=∠BODʹ，
∴△AOCʹ∽△BODʹ，
∴∠OACʹ=∠OBDʹ．
∵∠AFO=∠BFE，
∴∠AEB=∠AOB=θ．
24. （1） ∵ 四边形 ABCD 是矩形，
∴AB∥CD．
∴∠OAE=∠OCF，∠OEA=∠OFC．
∵AE=CF，
∴△AEO≌△CFO ASA．
∴OE=OF．
（2） 如图，连接 BO．
∵OE=OF，BE=BF，
∴BO⊥EF，且 ∠EBO=∠FBO．
∴∠BOF=90∘．
∵ 四边形 ABCD 是矩形，
∴∠BCF=90∘．
又 ∠BEF=2∠BAC，∠BEF=∠BAC+∠EOA，
∴ ∠BAC=∠EOA．
∴ AE=OE，
∵AE=CF，OE=OF，
∴OF=CF．
又 BF=BF，
∴△BOF≌△BCF HL．
∴∠OBF=∠CBF．
∴∠CBF=∠FBO=∠OBE．
∵∠ABC=90∘，
∴∠OBE=30∘．
∴∠BEO=60∘，
∴∠BAC=30∘．
∵tan∠BAC=BCAB，
∴tan30∘=23AB，即 33=23AB，
∴AB=6．
25. （1） 令 y=0，则 ax2+a+cx+c=0，解得 x=−ca 或 x=−1，
∴ 抛物线过 x 轴上的定点 A−1,0．
（2） 情况1：如图1，点 C 在点 A 右侧时，
∵ 四边形 PAQC 是平行四边形，
∴ 点 C 恰与点 B 重合，
∵P0,−3，
∴Q0,3，
抛物线的解析式为 y=ax2+3，
把 A−1,0 代入，得 a=−3，
∴y=−3x2+3．
情况2：如图2，点 C 在点 A 左侧时，
∵ 四边形 PACQ 是平行四边形，
∴PA=CQ，
由抛物线对称性可知 CQ=AQ，
∴PA=AQ，
∴ 点 A 在 PQ 的垂直平分线上，
∴PQ=2OA=2，
∴Q−2,−3，
设抛物线解析式为 y=ax+22−3，
把 A−1,0 代入，得 a=3，
∴y=3x+22−3，
综上所述，存在抛物线解析式为 y=−3x2+3 或 y=3x+22−3．