2020-2021学年北京市石景山区九上期末数学试卷

这是一份2020-2021学年北京市石景山区九上期末数学试卷，共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共8小题；共40分）
1. 已知 3a=4bab≠0，则下列各式正确的是
A. ab=43B. ab=34C. a3=b4D. a3=4b

2. 在 △ABC 中，∠C=90∘，tanA=2，则 sinA 的值是
A. 23B. 13C. 255D. 55

3. 如图所示，将一根长 2 m 的铁丝首尾相接围成矩形，则矩形的面积与其一边满足的函数关系是
A. 正比例函数关系B. 一次函数关系
C. 二次函数关系D. 反比例函数关系

4. 如图，PA，PB 为 ⊙O 的两条切线，点 A，B 是切点，OP 交 ⊙O 于点 C，交弦 AB 于点 D．下列结论中错误的是
A. PA=PBB. AD=BD
C. OP⊥ABD. ∠PAB=∠APB

5. 下列函数中，当 x>0 时，y 随 x 的增大而减小的是
A. y=x2B. y=2xC. y=−3xD. y=4x

6. 不透明的袋子中有三个小球，上面分别写着数字“1”，“2”，“3”，除数字外三个小球无其他差别．从中随机摸出一个小球，记录其数字，放回并摇匀，再从中随机摸出一个小球，记录其数字，那么两次记录的数字之和为 4 的概率是
A. 14B. 13C. 12D. 23

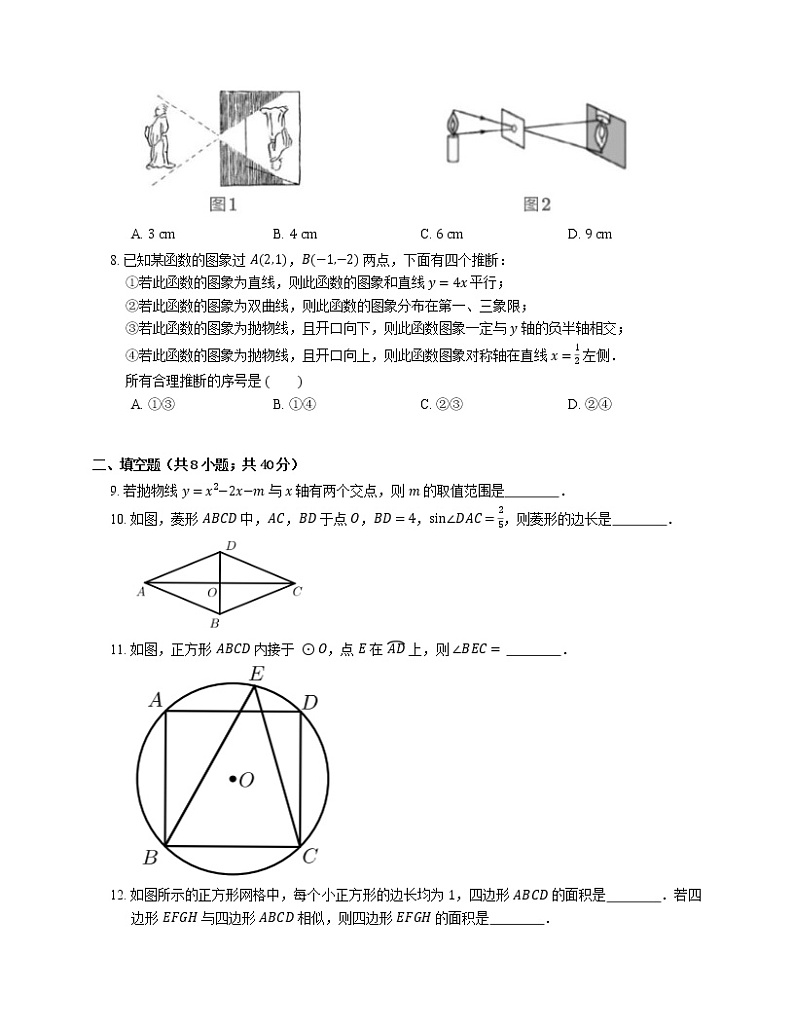
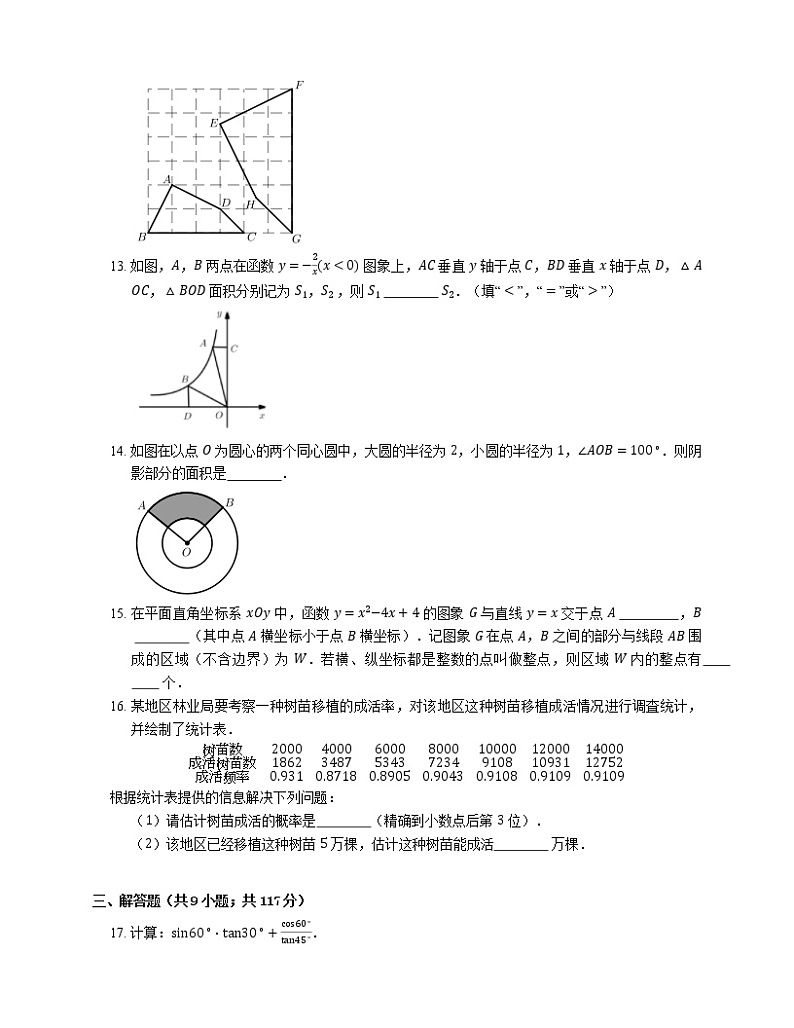
7. 大约在两千五百年前，如图 1 墨子和他的学生做了世界上第一个小孔成像的实验．并在《墨子经》中有这样的精彩记录：“景到，在午有端，与景长，说在端”．如图 2 所示的小孔成像实验中，若物距为 10 cm，像距为 15 cm，蜡烛火焰倒立的像的高度是 6 cm，则蜡烛火焰的高度是
A. 3 cmB. 4 cmC. 6 cmD. 9 cm

8. 已知某函数的图象过 A2,1，B−1,−2 两点，下面有四个推断：
①若此函数的图象为直线，则此函数的图象和直线 y=4x 平行；
②若此函数的图象为双曲线，则此函数的图象分布在第一、三象限；
③若此函数的图象为抛物线，且开口向下，则此函数图象一定与 y 轴的负半轴相交；
④若此函数的图象为抛物线，且开口向上，则此函数图象对称轴在直线 x=12 左侧．
所有合理推断的序号是
A. ①③B. ①④C. ②③D. ②④

二、填空题（共8小题；共40分）
9. 若抛物线 y=x2−2x−m 与 x 轴有两个交点，则 m 的取值范围是 ．

10. 如图，菱形 ABCD 中，AC，BD 于点 O，BD=4，sin∠DAC=25，则菱形的边长是 ．

11. 如图，正方形 ABCD 内接于 ⊙O，点 E 在 AD 上，则 ∠BEC= ．

12. 如图所示的正方形网格中，每个小正方形的边长均为 1，四边形 ABCD 的面积是 ．若四边形 EFGH 与四边形 ABCD 相似，则四边形 EFGH 的面积是 ．

13. 如图，A，B 两点在函数 y=−2xx<0 图象上，AC 垂直 y 轴于点 C，BD 垂直 x 轴于点 D，△AOC，△BOD 面积分别记为 S1，S2 ，则 S1 S2．（填“<”，“=”或“>”）

14. 如图在以点 O 为圆心的两个同心圆中，大圆的半径为 2，小圆的半径为 1，∠AOB=100∘．则阴影部分的面积是 ．

15. 在平面直角坐标系 xOy 中，函数 y=x2−4x+4 的图象 G 与直线 y=x 交于点 A ，B （其中点 A 横坐标小于点 B 横坐标）．记图象 G 在点 A，B 之间的部分与线段 AB 围成的区域（不含边界）为 W．若横、纵坐标都是整数的点叫做整点，则区域 W 内的整点有 个．

16. 某地区林业局要考察一种树苗移植的成活率，对该地区这种树苗移植成活情况进行调査统计，并绘制了统计表．
树苗数2000400060008000100001200014000成活树苗数186234875343723491081093112752成活频率
根据统计表提供的信息解决下列问题：
（1）请估计树苗成活的概率是 （精确到小数点后第 3 位）．
（2）该地区已经移植这种树苗 5 万棵，估计这种树苗能成活 万棵．

三、解答题（共9小题；共117分）
17. 计算：sin60∘⋅tan30∘+cs60∘tan45∘．

18. 已知关于 x 的二次函数 y=x2−m−2x−3．
（1）该函数图象经过点 2,−3．
①求这个二次函数的表达式及顶点坐标．
②分别求出这个二次函数图象与 x 轴，y 轴的交点坐标．
（2）将这个二次函数的图象沿 x 轴平移，使其顶点恰好落在 y 轴上，请直接写出平移后的函数表达式．

19. 下面是小石设计的”过圆上一点作圆的切线“的尺规作图的过程．
已知：如图 1，⊙O 及 ⊙O 上一点 P．
求作：直线 PN，使得 PN 与 ⊙O 相切．
作法：如图 2，
①作射线 OP；
②在 ⊙O 外取一点 Q（点 Q 不在射线 OP 上），以 Q 为圆心，QP 为半径作圆，⊙Q 与射线 OP 交于另一点 M；
③连接 MQ 并延长交 ⊙Q 于点 N；
④作直线 PN．
∴ 直线 PN 即为所求作直线．
根据小石设计的尺规作图的过程．
（1）使用直尺和圆规，补全图形（保留作图痕迹）；
（2）完成下面证明．
∵MN 是 ⊙Q 的直径，
∴∠MPN= ∘（ ）（填推理的依据）．
∴OP⊥PN．
又 ∵OP 是 ⊙O 的半径，
∴PN 是 ⊙O 的切线（ ）（填推理的依据）．

20. 如图，△ABC 中，D 是 AB 边上任意一点，F 是 AC 中点，过点 C 作 CE∥AB 交 DF 的延长线于点 E，连接 AE，CD．
（1）求证：四边形 ADCE 是平行四边形；
（2）若 ∠B=30∘，∠CAB=45∘，AC=6，CD=BD，求 AD 的长．

21. 在平面直角坐标系 xOy 中，直线 l:y=x−3 与函数 y=kxk≠0,x>0 的图象交于点 A4,t．
（1）求 t，k 的值．
（2）点 B 是函数 y=kxk≠0,x>0 的图象上任意一点（不与点 A 重合），点 P，Q 在直线 l 上，点 P 横坐标为 2．若 S△ABQ≥12S△ABP，求点 Q 横坐标的取值范围．

22. 如图，DO 是 ⊙O 的半径，点 F 是直径 AC 上一点，点 B 在 AD 的延长线上，连接 BC，使得 ∠ABC=12∠AOD．
（1）求证：BC 是 ⊙O 的切线．
（2）连接 BF，若 AD=165，tan∠ABC=43，BF=10，求 CF 的长．

23. 已知关于 x 的二次函数 y=x2−2tx+2．
（1）求该抛物线的对称轴（用含 t 的式子表示）．
（2）若点 Mt−3,m，Nt+5,n 在抛物线上，则 m n．（用“<”，“=”，或“>”填空）
（3）Px1,y1，Qx2,y2 是抛物线上的任意两个点，若对于 −1≤x1≤3 且 x2=3，都有 y1≤y2，求 t 的取值范围．

24. 已知矩形 MBCD 的顶点 M 是线段 AB 上一动点，AB=BC，矩形 MBCD 的对角线交于点 O，连接 MO，BO．点 P 为射线 OB 上一动点（与点 B 不重合），连接 PM，作 PN⊥PM 交射线 CB 于点 N．
（1）如图 1，当点 M 与点 A 重合时，且点 P 在线段 OB 上．
①依题意补全图 1，
②写出线段 PM 与 PN 的数量关系并证明．
（2）如图 2，若 ∠OMB=α，当点 P 在 OB 的延长线上时，请补全图形并直接写出 PM 与 PN 的数量关系．

25. 对于平面直角坐标系 xOy 中第一象限内的点 Px,y 和图形 W，给出如下定义：过点 P 作 x 轴和 y 轴的垂线，垂足分别为 M，N，若图形 W 中的任意一点 Qa,b 满足 a≤x 且 b≤y，则称四边形 PMON 是图形 W 的一个覆盖，点 P 为这个覆盖的一个特征点．例：已知 A1,2，B3,1，则点 P5,4 为线段 AB 的一个覆盖的特征点．
（1）已知点 C2,3 ，
①在 P11,3，P23,3，P34,4 中，是 △ABC 的覆盖特征点的为 ．
②若在一次函数 y=mx+5m≠0 的图象上存在 △ABC 的覆盖的特征点，求 m 的取值范围．
（2）以点 D2,4 为圆心，半径为 1 作圆，在抛物线 y=ax2−5ax+4a≠0 上存在 ⊙D 的覆盖的特征点，直接写出 a 的取值范围 ．
答案
第一部分
1. A【解析】∵3a=4b，
∴ab=43，a4=b3．
故 B，C，D错误．
故选A．
2. C【解析】△ABC 中 ∠C=90∘，tanA=BCAC=2，
设 AC=x，则 BC=2x，
∴AB=AC2+BC2=5x，
∴sinA=BCAB=2x5x=255．
3. C【解析】设一边长为 x m，面积为 y m2，
则另一边长为 2÷2−x=1−x m，
∴y=x1−x，x=−x2+x，
为二次函数关系．
4. D【解析】如图所示，连接 OA，OB，
∵PA 切 ⊙O 于 A，PB 切 ⊙O 于 B，
由切线长定理知，∠1=∠2，PA=PB，AD=BD，
∴△ABP 是等腰三角形，
∵∠1=∠2，
∴AB⊥OP，
故A，B，C正确．
∵△ABP 是等腰三角形，
∴∠PAB=∠PBA，
但不能证明 ∠PAB=∠APB．
故D错误，
故选D．
5. D
【解析】A选项：k>0，y 随 x 增大而增大，故A错误；
B选项：k>0，y 随 x 增大而增大，故B错误；
C选项：在每一个分支，y 随 x 增大而增大，故C错误；
D选项：y=4x，当 x>0 时，y 值随 x 值的增大而减小，故D正确．
6. B【解析】画树状图如下：
由树状图知，共有 9 种等可能结果，其中两次摸出的小球所标数字之和为 4 的有 3 种结果，
∴ 两次摸出的小球所标数字之和为 4 的概率为 39=13．
7. B【解析】根据题意画图如下：
∵ AB∥AʹBʹ，
∴△ABO∽△AʹBʹO，
则 ABAʹBʹ=OBOBʹ，
即 1015=OB6，
解得：OB=4 cm．
8. D【解析】①若此函数图象为直线，设该函数解析式为 y=kx+b，
将点 A2,1，B−1,−2 代入解析式得：2k+b=1，−k+b=−2，
解得：k=1，b=−1，
该函数解析式为：y=x−1，1≠4，
∴ 该函数图象和直线 y=4x 不平行，故①错误；
②若此函数图象为双曲线，根据双曲线得性质可知，点 A2,1 在第一象限，
点 B−1,−2 在第三象限，则此函数图象分布在第一，三象限，故②正确；
③若此函数图象为抛物线，且开口向下，经过第一象限的点 A2,1 和在第三象限点 B−1,−2，则此函数图象一定与 y 轴的正半轴相交，故③错误；
④若此函数图象为抛物线，且开口向上，设该函数解析式为 y=ax2+bx+c 且 a>0，函数图象经过点 A2,1，B−1,−2，
∴4a+2b+c=1，a−b+c=−2，
解得：c=−2a−1，b=−a+1，
对称轴为直线 x=−b2a=a−12a=12−12<12，
则此函数的对称轴在直线 x=12 左侧，故④正确；
∴ 合理推断的序号为②④．
第二部分
9. m>−1
【解析】∵y=x2−2x−m 与 x 轴有两个交点，
∴ 令 y=0 得 x2−2x−m=0，
∴Δ=−22−4×1×−m>0，
4+4m>0，
m>−1．
10. 5
【解析】在菱形 ABCD 中，
∵ 菱形的对角线互相垂直平分，
∴∠AOD=90∘，
OD=12BD=2，
∵sinDAC=ODAD=25，
∴2AD=25，
则 AD=5，
即菱形的边长为：5．
11. 45∘
【解析】连接 OB，OC，
则 ∠E=12∠BOC，
∵O 是正方形外接圆的圆心，
∴∠BOC=90∘，
∴∠BEC=12∠BOC=45∘
12. 92，818
【解析】SABCD=2×4−12×2×1−12×2×1−1×1−12×1×1=8−1−1−1−12=92,
∵ 四边形 EFGH 与四边形 ABCD 相似，
∴SEFGHSABCD=FGBC2=642，
∴SEFGH=94×92=818．
13. =
【解析】∵ AC⊥x轴，BD⊥y轴，
点 A，B 在反比列函数 y=−2x 图象上，
∴S1=12×∣−2∣=1，
S2=12×∣−2∣=1，
∴S1=S2．
14. 56π
【解析】S阴影=100360π22−12=56π.
15. 1,1，4,4，2
【解析】根据题意函数 y=x2−4x+4 与直线 y=x 有交点，
则有 x=x2−4x+4，
解得 x1=1，x2=4，
将 x1=1，x2=4 代入函数得两交点坐标分别为 1,1，4,4，
∵ 点 A 横坐标小于点 B 横坐标，
∴ 点 A 的坐标为 1,1，点 B 的坐标为 4,4，
将抛物线变形为顶点式：y=x−22，
即抛物线的顶点为 2,0，
将抛物线在直交系内描点如下：
则区域 W 内的整点数为有 2 个．
16. 0.911，4.555
【解析】（1）这种树苗成活的频率稳定在 0.911，成活的概率估计值为 0.911．
（2）估计这种树苗成活在 5×0.911=4.555 万棵．
答：估计这种树苗能成活 4.555 万棵．
第三部分
17. 原式=32×33+12÷1=1.
18. （1） ① ∵ 关于 x 的函数 y=x2−m−2x−3 经过点 2,−3，
把 2,−3 代入 y=x2−m−2−3，
则有 −3=22−2m−2−3，
−3=4−2m+4−3，
−m=4．
则二次函数的解析式为：y=x2−4−2x−3=x2−2x−3=x−12−4．
故顶点坐标为：1,−4．
②令 x=0，则 y=−3，
令 y=0，则 x2−2x−3=0，
x−3x+1=0，
x1=−1，x2=3．
故二次函数图象与 x 轴交点坐标为 −1,0，3,0．
与 y 轴交点坐标为：0,−3．
（2） y=x2−m24+m−4．
【解析】y=x2−m−2x−3 沿 x 轴平移，使其顶点落在 y 轴，则有
y=x2−m−2x+m−222−m−222−3=x−m−222−m24+m−4.
当 m−22=0 时，即抛物线 y=x2−m24+m−4 顶点在 y 轴上．
19. （1） 补全图形如下图：
（2） 90；直径所对的圆周角是直角；经过半径的外端，并且垂直于这条半径的直线是圆的切线
20. （1） ∵AB∥CE，
∴∠CAD=∠ACE，∠ADE=∠CED，
∵F是AC中点，
∴AF=CF，
在 △AFD 和 △CFE 中，
∠AFD=∠CFE,AF=CF,∠FAD=∠FCE
∴△AFD≌△CFE，
∴AD=CE，
∴ 四边形 ADCE 是平行四边形．
（2） 过点 C 作 CG⊥AB 于点 G，
∵CD=BD，∠B=30∘，
∴∠DCB=∠B=30∘，
∴∠CDA=60∘，
在 △ACG 中，∠AGC=90∘，AC=6，∠CAG=45∘，
∴CG=AG=3，
在 △CGD 中，∠DGC=90∘，∠CDG=60∘，CG=3，
∴GD=1，
∴AD=AG+GD=3+1．
21. （1） ∵ 点 A4,t 在直线 l:y=x−3 上，
∴t=1．
∵ 函数 y=kxk≠0,x>0 的图象经过点 A4,1，
∴k=4．
（2） 设点 B 到直线 AP 的距离为 h．
∴S△ABQ=12⋅AQ⋅h，S△ABP=12⋅AP⋅h，
∵S△ABQ≥12S△ABP，
∴AQ≥12AP．
∵A4,1，点 P 横坐标为 2，
如图 1，当点 Q 在射线 AP 上时，xQ≤3；
如图 2，当点 Q 在线段 PA 延长线上时，xQ≥5．
综上所述：点 Q 横坐标的取值范围 xQ≤3 或 xQ≥5．
22. （1） 连接 CD，
∵AD=AD，
∴∠ACD=12∠AOD，
∵∠ABC=12∠AOD，
∴∠ACD=∠ABC，
∵AC 是 ⊙O 直径，
∴∠ADC=90∘，
∴∠ABC+∠BCD=90∘，
∴∠BCA=∠BCD+∠ACD=90∘，
∴BC⊥AC，
∴BC 是 ⊙O 的切线．
（2） 在 △ACD 中，∠ADC=90∘，AD=165，tan∠ACD=tan∠ABC=43，
∴AC=4，
在 △ABC 中，∠ACB=90∘，tan∠ABC=43，AC=4，
∴BC=3，
在 △BCF 中，∠BCF=90∘，BF=10，BC=3，
∴CF=BF2−BC2=1．
23. （1） ∵ y=x2−2tx+2=x−t2+2−t2，
∴ 该抛物线的对称轴为直线 x=t．
（2） <
【解析】∵ 抛物线开口向上，
∴ 抛物线图象上的点到对称轴的距离越远，函数值越大，
∴ Mt−3,m，Nt+5,n 在抛物线上，
∴ M 点到对称轴的距离为 3，N 点到对称轴的距离为 5，
∴ m （3） 当 t≤1 时，此时 −1≤x1<3，x2=3 都有 y1≤y2，符合题意；
当 t>1 时，令 x1=−1 时，y1>y2，不符合题意．
综上所述：t≤1．
24. （1） ①补全图形如图 1，
②线段 PM 与 PN 的数量关系为：PM=PN．
证明：过点 P 分别作 PG⊥MB 于 G，PH⊥BC 于 H，线段 PN 交 MB 于点 F．如图 2．
∵ 四边形 MBCD 是矩形，AB=BC，
∴ 四边形 MBCD 是正方形．
∴BO 平分 ∠MBC，∠MBC=90∘．
∵PG⊥MB，PH⊥BC，
∴PG=PH，∠PHB=∠PGM=90∘．
∵PM⊥PN，∠MBC=90∘，
∴∠MPN=∠GBN=90∘．
∵∠MFP=∠BFN，
∴∠PMG=∠PNH．
在 △PMG 和 △PNH 中，
∠PMG=∠PNH,∠PGM=∠PHN,PG=PH,
∴△PMG≌△PNHAAS．
∴PM=PN．
（2） 补全图形如图 3．
PM 与 PN 的数量关系为：PMPN=tanα．
【解析】过点 P 作 PG⊥BP 交 CN 于点 G，如图 4．
∵ 矩形 MBCD 的对角线交于点 O，
∴OB=OM，
∴∠OBM=∠OMB=α，
∵∠MBN=90∘，
∴∠OBM+∠PBG=90∘，
∵PG⊥BP，
∴∠PBG+∠PGB=90∘，
∴∠OBM=∠PGB=α，
∵PM⊥PN，
∴∠MPN=∠BPG=∠MBN=90∘，
∴∠BPM=∠GBN，
∠BMP=∠GNP，
∴△PBM∽△PGN，
∴PMPN=PBPG，
∵tan∠PGB=tanα=PBPG，
∴PMPN=tanα．
25. （1） ① P23,3；P34,4
②当 m>0 时，结合函数图象可知符合题意．
当 m<0 时，由题意得：
当 x≥3 且 y≥3 时，
点 Px,y 为 △ABC 的覆盖的特征点．
又 ∵ 点 P 在一次函数 y=mx+5m≠0 的图象上，
∴ 当直线 y=mx+5m≠0 过点 K3,3 时，
解得：m=−23，
∴ 结合函数图象可知 −23≤m<0，
综上所述：m≥−23 且 m≠0．
【解析】① ∵A1,2，B3,1，C2,3，
画出 △ABC，
由题意结合图形可知，
当 x≥3 且 y≥3 时，
点 Px,y 为 △ABC 的覆盖的特征点．
所以在 P11,3，P23,3，P34,4 中，是 △ABC 的覆盖特征点的为 P23,3，P34,4．
（2） a>0 或 a≤−16
【解析】∵ 以 D2,4 为圆心，半径为 1 作圆，
∴ 当 x≥3 且 y≥5 时，点 Px,y 即为 ⊙D 的覆盖的特征点．
∴ 当 a>0 时，抛物线开口向上，
故抛物线图象上存在 ⊙D 的覆盖的特征点．
当 a<0 时，将 M3,5 代入抛物线 y=ax2−5ax+4 中得：9a−15a+4=5，解得：a=−16，
∴ 当 a≤−16 时，抛物线图象上也存在 ⊙D 的覆盖的特征点．
∴a 的取值范围是 a>0 或 a≤−16．