2021年北京石景山区北京市九中九年级上期末数学试卷

这是一份2021年北京石景山区北京市九中九年级上期末数学试卷，共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共8小题；共40分）
1. 一元二次方程 4x2+1=4x 的根的情况是
A. 有实数根B. 有两个相等的实数根
C. 有两个不相等的实数根D. 没有实数根

2. 如图，在 Rt△ABC 中，∠C=90∘，三边分别为 a，b，c，则 csA 等于
A. acB. abC. baD. bc

3. A、B、C、D 四名选手参加 50 米决赛，赛场共设 1，2，3，4 四条跑道，选手以随机抽签的方式决定各自的跑道，若 A 首先抽签，则 A 抽到 1 号跑道的概率是
A. 1B. 12C. 13D. 14

4. 如图，桌子上放着一个圆柱和一个长方体，从上面看到的平面图形应是
A. B.
C. D.

5. 若 x1,y1，x2,y2 都是 y=−5x 的图象上的点，且 x1A. y1>y2>0B. y1y1>0D. y2<0
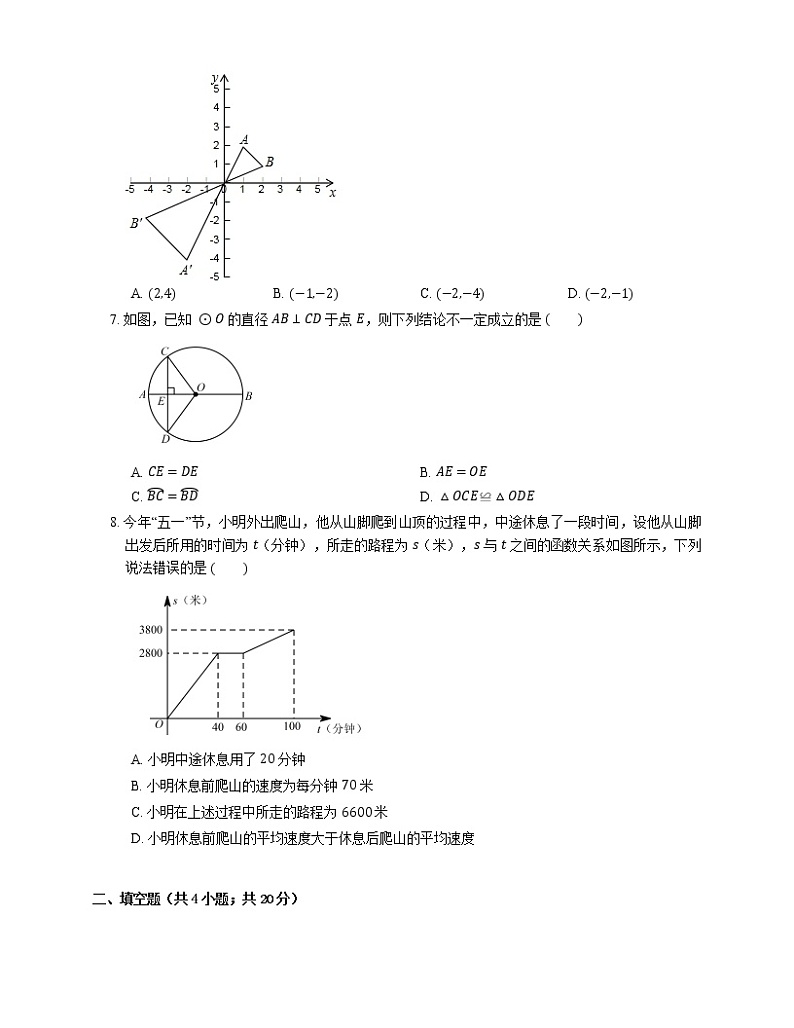
6. 如图，在平面直角坐标系中，以原点 O 为位中心，将 △ABO 扩大到原来的 2 倍，得到 △AʹBʹO．若点 A 的坐标是 1,2，则点 Aʹ 的坐标是
A. 2,4B. −1,−2C. −2,−4D. −2,−1

7. 如图，已知 ⊙O 的直径 AB⊥CD 于点 E，则下列结论不一定成立的是
A. CE=DEB. AE=OE
C. BC=BDD. △OCE≌△ODE

8. 今年“五一”节，小明外出爬山，他从山脚爬到山顶的过程中，中途休息了一段时间，设他从山脚出发后所用的时间为 t（分钟），所走的路程为 s（米），s 与 t 之间的函数关系如图所示，下列说法错误的是
A. 小明中途休息用了 20 分钟
B. 小明休息前爬山的速度为每分钟 70 米
C. 小明在上述过程中所走的路程为 6600 米
D. 小明休息前爬山的平均速度大于休息后爬山的平均速度

二、填空题（共4小题；共20分）
9. 如图，两圆圆心相同，大圆的弦 AB 与小圆相切，AB=8，则图中阴影部分的面积是 ．（结果保留 π）

10. 如图，小明在 A 时测得某树的影长为 3 米，B 时又测得该树的影长为 12 米，若两次日照的光线互相垂直，则树的高度为 米．

11. 已知二次函数 y=kx2+2k−1x−1 与 x 轴交点的横坐标为 x1 、 x2 x1x2 时，y>0；③ 方程 kx2+2k−1x−1=0 有两个不相等的实数根 x1 、 x2；④ x1<−1，x2>−1；⑤ x2−x1=1+4k2k，其中所有正确的结论是 （只填写顺号）．

12. 补全下列每列数：
① 2，4，6， ，10，⋯；
② 1，12，123，1234， ，123456，⋯；
③ 1，3，6， ，15，21，⋯；
④ 1，2，6， ，120，720，⋯；
⑤ 1，1，2，3，5， ，13，21，⋯．

三、解答题（共13小题；共169分）
13. 求值：tan60∘+1−32−π−3.140+27−2+3−1．

14. 如图，在 △ABC 中，∠ABC=2∠C，BD 平分 ∠ABC，且 AD=2，BD=22，求 AB 的值．

15. 一元二次方程 ax−12+bx−1+c=0 化为一般形式为 2x2−3x−1=0，试求 a+bc 的值．

16. 已知二次函数 y=m−2x2−4x+m2+2m−8 的图象经过原点，它可以由哪条顶点在原点的抛物线经过平移得到?说出平移的过程．

17. 如图，反比例函数 y=kxx>0 的图象经过 △OAB 的顶点 A 和 OB 的中点 C，AB∥x 轴，点 A 的坐标为 2,3．
（1）确定 k 的值；
（2）求 △OAB 的面积．

18. 如图，在 Rt△ABC 中，∠C=90∘，D 为 BC 上一点，AB=5，BD=1，tanB=34．
（1）求 AD 的长；
（2）求 sinα 的值．

19. 已知：关于 x 的方程 x2−k+2x+2k=0．
（1）求证：无论 k 取何值，方程总有实数根；
（2）若等腰三角形 ABC 的一条边长为 1，另两条边恰好是这个方程的两个根，求三角形 ABC 的周长．

20. 如图是泰州某河上一座古拱桥的截面图，拱桥桥洞上沿是抛物线形状，抛物线两端点与水面的距离都是 1 m，拱桥的跨度为 10 m，桥洞与水面的最大距离是 5 m，桥洞两侧壁上各有一盏距离水面 4 m 的景观灯．若把拱桥的截面图放在平面直角坐标系中（如图）．
（1）求抛物线的解析式；
（2）求两盏景观灯之间的水平距离．

21. 如图，AB 为 ⊙O 的直径，C 为 ⊙O 上一点，AD 和过 C 点的直线互相垂直，垂足为 D，且 AC 平分 ∠DAB．
（1）求证：DC 为 ⊙O 的切线；
（2）若 ⊙O 的半径为 3，AD=4，求 AC 的长．

22. 在平面直角坐标系 xOy 中，已知双曲线 y=kx 过点 A1,1，与直线 y=4x 交于 B，C 两点（点 B 的横坐标小于点 C 的横坐标）．
（1）求 k 的值．
（2）求点 B，C 的坐标．
（3）若直线 x=t 与双曲线 y=kx 交于点 Dt,y1，与直线 y=4x 交于点 Et,y2．当 y1
23. 如图，在 △ABC 和 △ADE 中，ABAD=BCDE=ACAE，点 B，D，E 在一条直线上．求证：△ABD∽△ACE．

24. 已知：如图，在 △ABC 中，AB=AC，∠BAC=α，且 60∘<α<120∘．P 为 △ABC 内部一点，且 PC=AC，∠PCA=120∘−α．
（1）用含 α 的代数式表示 ∠APC，得 ∠APC= ；
（2）直接写出 ∠BAP 与 ∠PCB 的大小关系是 ；
（3）求 ∠PBC 的度数．

25. 如图，在四边形 ABCD 中，对角线 AC，BD 相交于点 E，且 AC⊥BD，∠ADB=∠CAD+∠ABD，∠BAD=3∠CBD．
（1）求证：△ABC 为等腰三角形；
（2）M 是线段 BD 上一点，BM:AB=3:4，点 F 在 BA 的延长线上，连接 FM，∠BFM 的平分线 FN 交 BD 于点 N，交 AD 于点 G，点 H 为 BF 的中点，连接 MH，当 GN=GD 时，探究线段 CD，FM，MH 之间的数量关系，并证明你的结论．
答案
第一部分
1. B
2. D
3. D
4. B
5. C
【解析】∵ 反比例函数 y=−5x 中，k=−5<0，
∴ 此函数图象的两个分支在二、四象限，
∵x1 ∴ 两点在第二象限，
∵ 在第二象限内 y 的值随 x 的增大而增大，
∴06. C
7. B【解析】∵⊙O 的直径 AB⊥CD 于点 E，
∴CE=DE，CB=BD，
在 △OCE 和 △ODE 中，
∠CEO=∠DEO=90∘,∠OCE=∠ODE,OC=OD,
∴△OCE≌△ODE．
8. C【解析】小明在上述过程中所走的路程为 3800 米，
小明休息前爬山的平均速度 280040=70（米/分钟），
休息后爬山的平均速度 100040=25（米/分钟）．
第二部分
9. 16π
【解析】S阴影=πR2−πr2=πR2−r2=π×42=16π.
10. 6
【解析】如图，因为 ∠CDF=∠FDE=∠CFE=90∘，
所以 ∠CFD+∠DFE=90∘，∠DCF+∠DFC=90∘．
所以 ∠DFE=∠DCF．
所以 △DFE∽△DCF．
所以 DFDC=DEDF．
所以 DF2=DE⋅DC=36．
所以 DF=6 米．
11. ①③④
【解析】① 将 x=−2 带入函数解析式即可；
② 不对，因为不确定 k 的正负；
③ 函数与 x 轴有两个交点则一元二次方程即有两个根；
④ 由根系关系得 x1+x2=1−2kk，x1x2=−1k，
∴x1+1x2+1=x1x2+x1+x2+1=−1k+1−2kk+1=−1.
∴x1+1x2+1<0．
∵x1 ∴x1+1<0，x2+1>0．
∴x1<−1，x2>−1．
⑤ 不确定 k 的正负所以不对，正确的应将 k 加绝对值．
12. ①8，②12345，③10，④24，⑤8
【解析】①是由所有偶数从小到大排列而成．
②数的特点是：是第几个数，它的数位上的数从大到小分别是从 1 到几．
③ 1 和 3 之间差 2，3 和 6 之间差 3，15 和 21 之间差 6，猜测 6 和 ，以及 和 15 之间应该分别差 4 和 5，得到答案为 10．
④ 1×2=2，2×3=6，120×6=720，猜测 6 和 以及 和 120 之间分别差 4 倍和 5 倍．
⑤ 1+1=2，1+2=3，2+3=5，推测 5+ =13．
第三部分
13. tan60∘+1−32−π−3.140+27−2+3−1=3+4−23−1+33−2−3=4−1−2+43−23+3=1+33
14. ∵BD 平分 ∠ABC，
∴∠ABC=2∠ABD=2∠DBC．
∴∠C=∠ABD=∠DBC．
∴CD=BD=22．
∴AC=32．
∵∠A=∠A，
∴△ABD∽△ACB．
∴ADAB=ABAC．
∴AB2=AD⋅AC=2×32=6．
∴AB=6，AB=−6（舍去）．
∴AB=6．
15. 将方程 ax−12+bx−1+c=0 整理可得 ax2+b−2ax+a−b+c=0．
∵ 它的一般形式是 2x2−3x−1=0，
∴ 设 a=2kk≠0，则 b−2a=−3k，a−b+c=−k，
解得 a=2k,b=k,c=−2k,
∴a+bc=2k+k−2k=−32．
16. 由 m2+2m−8=0,m−2≠0 得 m=−4，
则 y=−6x2−4x=−6x+132+23，
该抛物线可以由抛物线 y=−6x2 先向左平移 13 个单位，再向上平移 23 个单位得到．
17. （1） ∵ 点 2,3 在反比例函数 y=kx 图象上，
∴ k=2×3=6．
（2） ∵ AB∥x 轴，C 为 OB 中点．A2,3，
∴ 点 C 的纵坐标为 32，
∵ C 在抛物线 y=6x 上，
∴ 32=6x，
∴ x=4，
∴ C4,23
∴ B8,3，
∴ S△OAB=128−2×3=9
18. （1） 因为 tanB=34，
所以可设 AC=3x，BC=4x，x>0．
因为 AC2+BC2=AB2，
所以 3x2+4x2=52，
所以 x=1，
所以 AC=3，BC=4．
因为 BD=1，
所以 CD=3，
所以 AD=CD2+AC2=32．
（2） 过点 D 作 DE⊥AB 于点 E，如图所示，
因为 tanB=34，
所以可设 DE=3y，BE=4y，y>0，
因为 BE2+DE2=BD2，
所以 3y2+4y2=12，
所以 y=15，
所以 DE=35，
所以 sinα=DEAD=210．
19. （1） 方程 x2−k+2x+2k=0 中，a=1，b=−k+2，c=2k，
则有 Δ=b2−4ac=k+22−4⋅2k=k−22≥0，恒成立，
所以方程总有实数根．
（2） 解 x2−k+2x+2k=0 得 x1=2,x2=k．
由题意知 x1，x2 对应三角形为等腰三角形，
则有 k=1 或 k=2．
同时根据三角形三边关系，知 k+1>2．
解得 k>1．则有 k=2．
三角形周长为 1+2+k=1+2+2=5．
20. （1） y=−425x−52+50≤x≤10．
（2） 5 米．
21. （1）
连接 OC．
∵OC=OA，
∴∠OAC=∠OCA．
又 ∠OAC=∠DAC，
∴∠DAC=∠OCA．
∴OC∥AD．
∴OC⊥CD，即 DC 为 ⊙O 的切线．
（2） 连接 BC．
由（1）知 △ADC∽△ACB，
∴ADAC=ACAB，即 AC2=AD⋅AB．
又 ⊙O 的半径为 3，
∴AB=6，
∵AD=4，
∴AC=26．
22. （1） ∵ 双曲线 y=kx 过点 A1,1，
∴ 把 x=1，y=1 代入得：1=k1，k=1，
故 k 的值为 1．
（2） 联立 y=1x,y=4x,
解得：4x=1x，4x2=1，x2=14，x=±12，
当 x1=12 时，y=2，
当 x2=−12 时，y=−2，
又 ∵ 点 B 的横坐标小于点 C 的横坐标，
∴B−12,−2，C12,2．
（3） 把 x=t 代入双曲线中得：y1=1t，
把 x=t 代入直线中得：y2=4t，
又 ∵y1 ∴1t<4t，
∵ 当 t<0 时，1>4t2，t2<14，−12 ∴−12 ∵ 当 t>0 时，1<4t2，t2>14，t<−12 或 t>12，
∴t>12，
故 t 的取值范围是 −1212．
23. ∵ 在 △ABC 和 △ADE 中，ABAD=BCDE=ACAE，
∴ △ABC∽△ADE，
∴ ∠BAC=∠DAE，
∴ ∠BAD=∠CAE．
∵ ABAD=ACAE，
∴ ABAC=ADAE，
∴ △ABD∽△ACE．
24. （1） 30∘+α2
【解析】提示：由 PC=AC，∠PCA=120∘−α，得 ∠APC=∠PAC=30∘+α2．
（2） ∠BAP=∠PCB
【解析】提示：∠BAP=∠BAC−∠PAC=α−30∘+α2=α2−30∘．
∵AB=AC，∠BAC=α，
∴∠ABC=∠ACB=90∘−α2．
∴∠PCB=∠ACB−∠ACP=α2−30∘．
（3） 在 CB 上截取 CM 使 CM=AP，连接 PM．

∵PC=AC，AB=AC，
∴PC=AB．
在 △ABP 和 △CPM 中，
AB=CP,∠3=∠4,AP=CM,
∴△ABP≌△CPM．
∴∠ABP=∠CPM，BP=PM．
∴∠6=∠7．
∵∠ABP=∠ABC−∠6，∠CPM=∠7−∠4，
∴∠ABC−∠6=∠7−∠4．
即 90∘−α2−∠6=∠7−α2−30∘．
∴∠6+∠7=60∘．
∴2∠6=60∘．
∴∠6=30∘．
即 ∠PBC=30∘．
25. （1） 如图，作 ∠BAP=∠DAE，AP 交 BD 于点 P．
∵∠ADB=∠CAD+∠ABD，∠APE=∠BAP+∠ABD，
∴∠APE=∠ADE，
∴AP=AD．
∵AC⊥BD，
∴∠PAE=∠DAE．
∴∠BAD=3∠DAE．
∵∠BAD=3∠CBD，
∴∠DAE=∠CBD．
∴∠ECB=∠ADE．
∵∠ABC=∠ABD+∠DBC=∠ABD+∠CAD=∠ADB，
∴∠ACB=∠ABC．
∴AB=AC，
∴△ABC 为等腰三角形．
（2） 2MH=FM+34CD．证明如下：
如图，由（1）知 AP=AD，AB=AC，∠BAP=∠CAD．
∴△ABP≌△ACD．
∴∠ABE=∠ACD．
∵AD=AP，GD=GN，
∴∠APD=∠ADP=∠GND，
∴AP∥FN．
∴∠BAP=∠BFN．
∵ FN 平分 ∠BFM，∠BAP=∠EAP，
∴∠BAE=∠BFM，
∴AC∥FM．
∴FM⊥BD．
∵ H 为 FB 的中点，
∴FB=2MH．
在 FB 上截取 FR=FM，连接 RM．
∴∠FRM=12180∘−∠RFM．
∵AB=AC，
∴∠ABC=12180∘−∠BAC，
∴∠FRM=∠ABC．
∴RM∥BC．
∴∠BMR=∠DBC=∠CAD．
∵∠RBM=∠DCA，
∴△RMB∽△DAC，
∴BRCD=BMAC=BMAB=34．
∴FB−FM=BR=34CD，
∴2MH=FM+34CD．