

华师大版九年级下册3. 切线优质教学课件ppt
展开
这是一份华师大版九年级下册3. 切线优质教学课件ppt,共25页。PPT课件主要包含了复习回顾,直线与圆相离,直线与圆相切,直线与圆相交,探究新知,我们可以发现,∵PA切⊙O于点A,∴OA⊥PA,同理可得OB⊥PB,切线长定理等内容,欢迎下载使用。
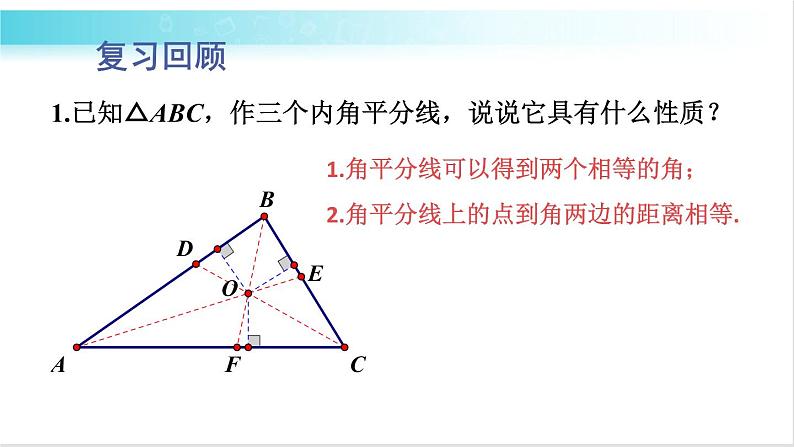
1.已知△ABC,作三个内角平分线,说说它具有什么性质?
1.角平分线可以得到两个相等的角;
2.角平分线上的点到角两边的距离相等.
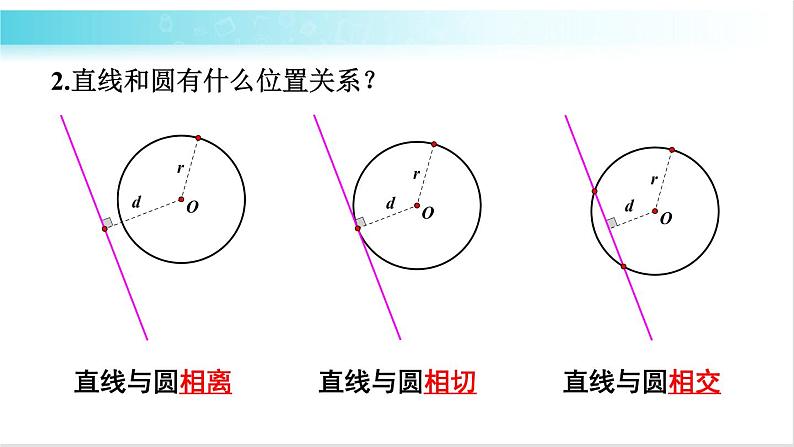
2.直线和圆有什么位置关系?
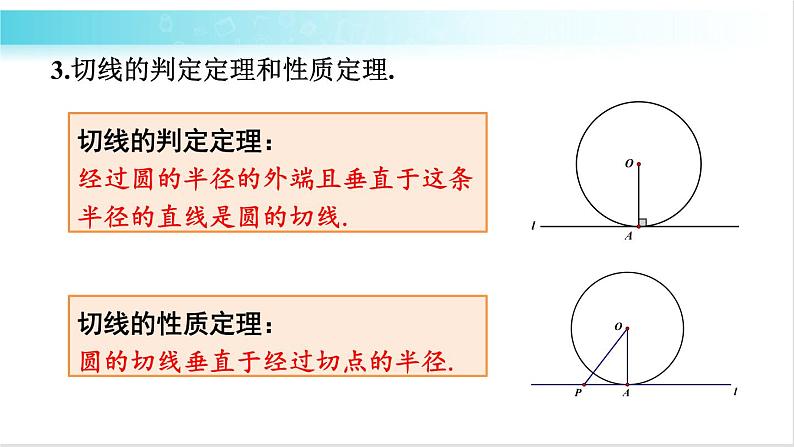
3.切线的判定定理和性质定理.
切线的判定定理:经过圆的半径的外端且垂直于这条半径的直线是圆的切线.
切线的性质定理:圆的切线垂直于经过切点的半径.
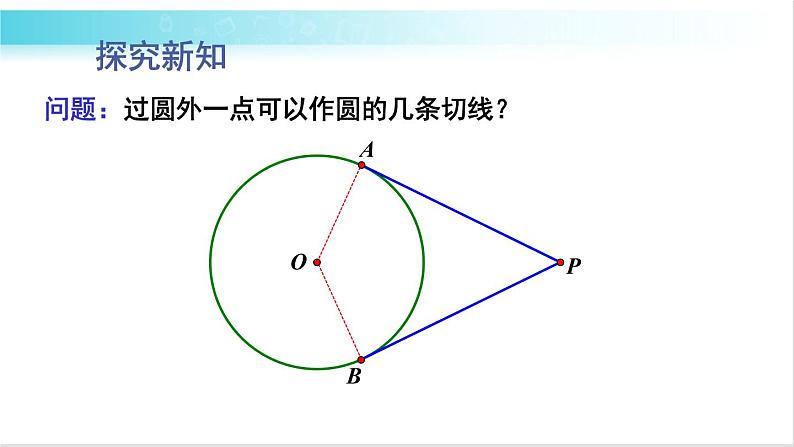
问题:过圆外一点可以作圆的几条切线?
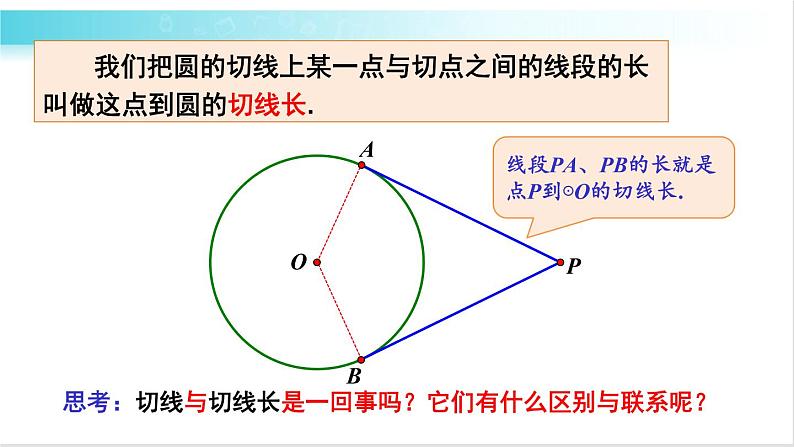
我们把圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长.
线段PA、PB的长就是点P到⊙O的切线长.
思考:切线与切线长是一回事吗?它们有什么区别与联系呢?
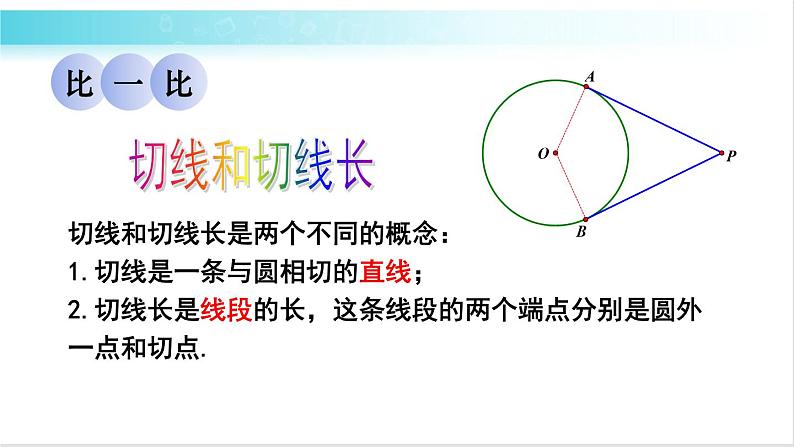
切线和切线长是两个不同的概念:1.切线是一条与圆相切的直线;2.切线长是线段的长,这条线段的两个端点分别是圆外一点和切点.
在纸上画出如图所示的图形,沿着直线PO将纸对折,由于直线PO经过圆心O,所以PO是圆的一条对称轴,两半圆重合.PA与PB、∠APO与∠BPO有什么关系?
PA=PB,∠APO=∠BPO.
请证明你所发现的结论.
已知:如图所示,PA、PB是⊙O的两条切线,切点分别为A、B.求证:PA=PB,∠APO=∠BPO.
证明:连结OA和OB.
∵OA=OB,OP=OP,
∴Rt△OAP≌Rt△OBP,
∴PA=PB,∠APO=∠BPO.
过圆外一点所画的圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
PA、PB分别切⊙O于A、B
切线长定理为证明线段相等、角相等提供新的方法.
若连结两切点A、B,AB交OP于点M.你又能得出什么新的结论?并给出证明.
证明:∵PA,PB是⊙O的切线,点A,B是切点,∴PA=PB,∠OPA=∠OPB.∴△PAB是等腰三角形,PM为顶角的角平分线.∴OP垂直平分AB.
探究:PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C.
(1)写出图中所有的垂直关系;
OA⊥PA,OB ⊥PB,AB ⊥OP.
(3)写出图中所有的全等三角形;
△AOP≌△BOP, △AOC≌△BOC, △ACP≌△BCP.
(4)写出图中所有的等腰三角形;
(2)写出图中与∠OAC相等的角和图中相等的线段;
∠OAC=∠OBC=∠APC=∠BPC,OA=OB=OD=OE,PA=PB,AC=BC.
如图所示是一张三角形铁皮,如何在它上面截取一个面积最大的圆形铁皮?
作圆,使它和已知三角形的各边都相切.
已知:△ABC(如图).求作:和△ABC的各边都相切的圆.
作法:1.作∠ABC,∠ACB的平分线BM和CN,交点为I.2.过点I作ID⊥BC,垂足为D.3.以I为圆心,ID为半径作⊙I,⊙I就是所求的圆.
与三角形三边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.
三角形的内心到三角形的三边距离相等.
一个三角形的内切圆是唯一的.
1.如图,⊙O是∠ABC的内切圆,与AB、BC、CA分别相切于点D、E、F,∠DOE=120°,∠EOF=150°.求∠ABC的三个内角的大小.
解:⊙O为△ABC的内切圆,且点D、E、F为切点.∴∠ODB=∠OEB=∠ODA=∠OFA=∠OFC= ∠OEC=90°,∴∠A=360°-∠DOF-∠ADO-∠AFO =360-(360°-120°-150°)-90°-90°= 90°, ∠B=360°-∠DOE-∠BDO-∠BEO=60°, ∠C=360°-∠EOF-∠CFO-∠CEO=30°.即△ABC的三个内角的度数分别为90°,60°,30°.
2.△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且AB=5cm,BC=9cm,CA=6cm.求AD、BE和CF的长.
解:设AD=x cm,BE=y cm,CF=z cm.∵⊙O与AB,BC,CA分别相切于点D,E,F,∴AD=AF=x cm,BE=BD=y cm,CE=CF=z cm, AB=AD+BD=5cm,BC=BE+EC=9cm,AC=CF+AF=6cm.
∴设AD=1cm,BE=4cm,CF=5cm.
3.任意画一个三角形,然后作出它的内切圆.
解:(1)任意画一个△ABC,分别作∠A,∠B(或∠A与∠C,或∠B与∠C)的平分线,两角平分线的交点O即为△ABC的内切圆的圆心. (2)过点O作OD⊥AB,则OD即为△ABC的内切圆的半径.(3)以点O为圆心,以OD为半径作⊙O,则⊙O即为所求作的内切圆,如图所示.
4.如图,AE、AD、BC分别切⊙O于点E、D、F,若AD= 20,求△ABC的周长.
解:∵AD,AE切于⊙O于D,E,∴AD=AE=20.∵AD,BF切于⊙O于D,F,∴BD=BF,同理:CF=CE.∴C△ABC= AB+BC+AC=AB+BF+FC+AC =AB+BD+EC+AC=AD+AE=40.
5.如图,PA、PB是⊙O的两条切线,切点分别为点A、B,若直径AC=12,∠P=60°,求弦AB的长.
切线长定理:过圆外一点所画的圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
1.从课后习题中选取;2.完成练习册本课时的习题.
相关课件
这是一份初中数学华师大版九年级下册3. 切线习题课件ppt,共23页。
这是一份华师大版九年级下册第27章 圆27.2 与圆有关的位置关系3. 切线教学课件ppt,共30页。
这是一份初中数学华师大版九年级下册第27章 圆27.2 与圆有关的位置关系3. 切线教学ppt课件,共21页。










