初中数学华师大版九年级下册第27章 圆27.2 与圆有关的位置关系3. 切线教学ppt课件

这是一份初中数学华师大版九年级下册第27章 圆27.2 与圆有关的位置关系3. 切线教学ppt课件，共21页。
　　　　　　　　　　　　　　　　
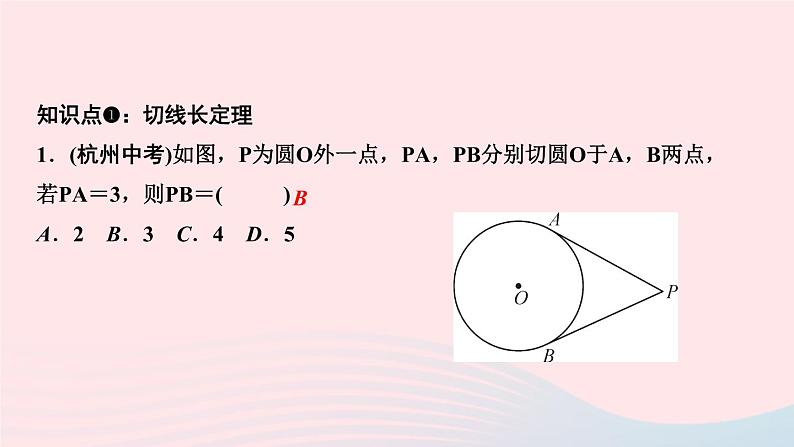
知识点❶：切线长定理1．(杭州中考)如图，P为圆O外一点，PA，PB分别切圆O于A，B两点，若PA＝3，则PB＝( )A．2 B．3 C．4 D．5
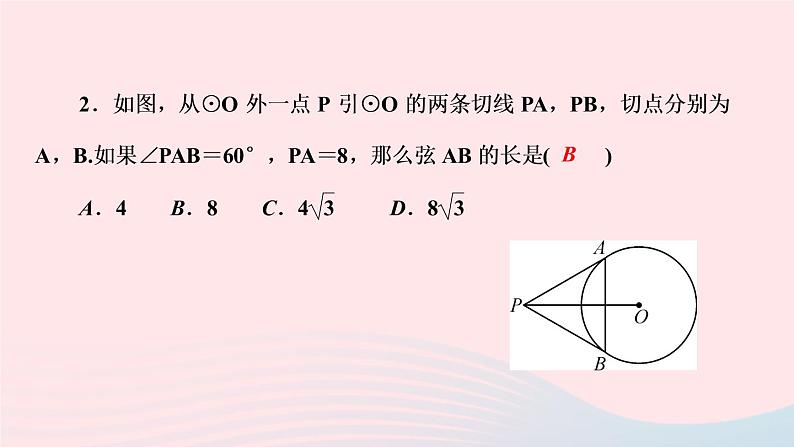
3．(2020·湘西州)如图，PA，PB为圆O的切线，切点分别为A，B，PO交AB于点C，PO的延长线交圆O于点D.下列结论不一定成立的是( )A.△BPA为等腰三角形B．AB与PD相互垂直平分C．点A，B都在以PO为直径的圆上D．PC为△BPA的边AB上的中线
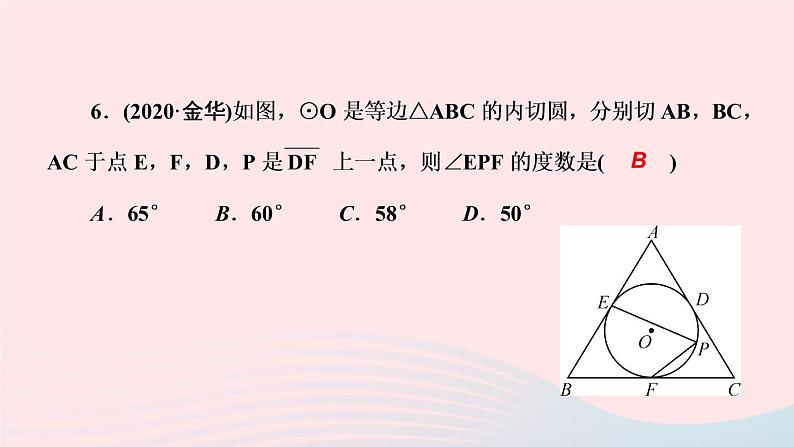
知识点❷：三角形的内切圆5．(习题2变式)《九章算术》是我国古代内容极为丰富的数学名著，书中有下列问题“今有勾八步，股十五步，问勾中容圆径几步？”其意思是：“如图，今有直角三角形，勾(短直角边)长为8步，股(长直角边)长为15步；问该直角三角形能容纳的圆形(内切圆)直径是多少？”( )A．3步 B．5步 C．6步 D．8步
9．(2020·青海)如图，在△ABC中，∠C＝90°，AC＝3，BC＝4，则△ABC的内切圆半径r＝____．
10．(2020·眉山)如图，点P为⊙O外一点，过点P作⊙O的切线PA，PB，点A，B为切点，连结AO并延长交PB的延长线于点C，过点C作CD⊥PO，交PO的延长线于点D.已知PA＝6，AC＝8，则CD的长为_________．
11．(天津中考)已知PA，PB分别与⊙O相切于点A，B，∠APB＝80°，C为⊙O上一点．(1)如图①，求∠ACB的大小；(2)如图②，AE为⊙O的直径，AE与BC相交于点D.若AB＝AD，求∠EAC的大小．
12．(习题12变式)如图，⊙O是△ABC的内切圆，与AB，BC，CA分别相切于点D，E，F，∠DEF＝45°.连结BO并延长交AC于点G，AB＝4，AG＝2.(1)求∠A的度数；(2)求⊙O的半径．
(1)证明：连结OC，如图①，∵AB是⊙O的直径，∴∠ACB＝90°，∴∠A＋∠B＝90°，∵OC＝OB，∴∠B＝∠OCB，∵∠BCM＝∠A，∴∠OCB＋∠BCM＝90°，即OC⊥MN，∴MN是⊙O的切线