
华师大版九年级下册3. 切线授课ppt课件
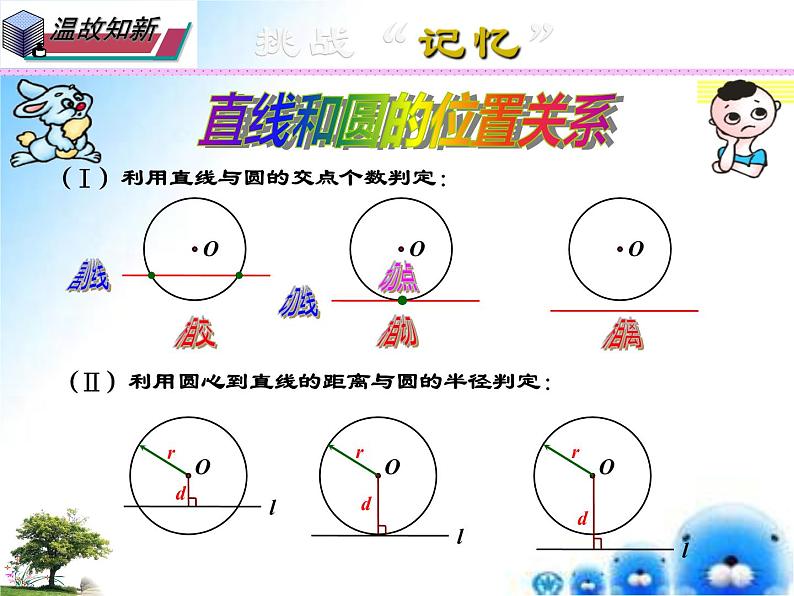
展开(Ⅰ)利用直线与圆的交点个数判定:
(Ⅱ)利用圆心到直线的距离与圆的半径判定:
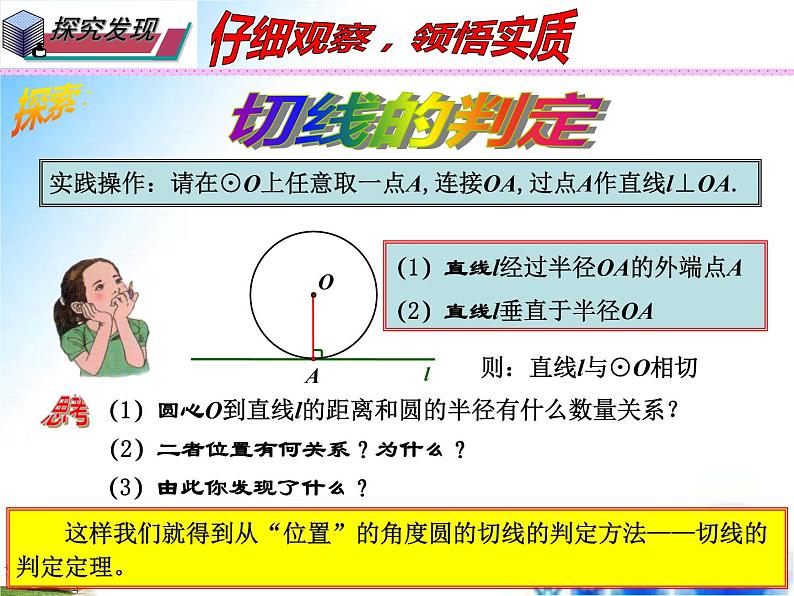
实践操作:请在⊙O上任意取一点A,连接OA,过点A作直线l⊥OA.
(3)由此你发现了什么?
(2)二者位置有何关系?为什么?
(1)直线l经过半径OA的外端点A
(2)直线l垂直于半径OA
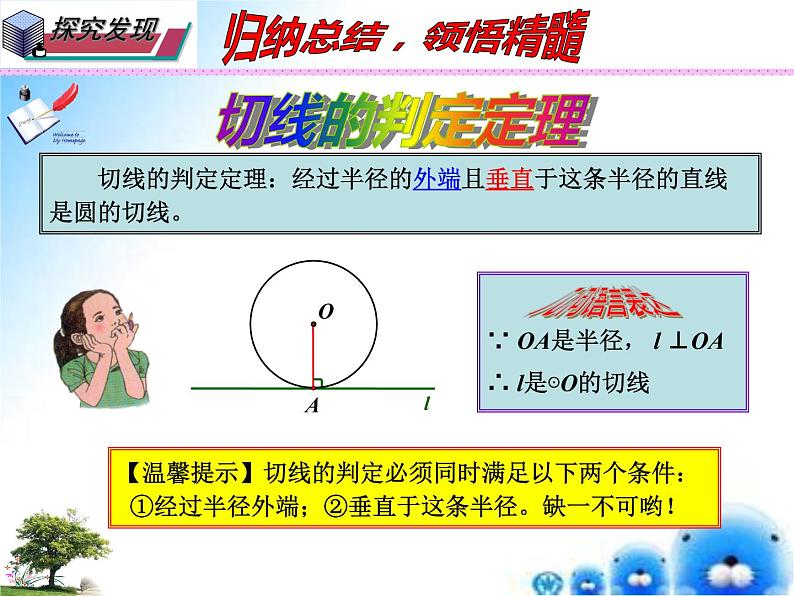
这样我们就得到从“位置”的角度圆的切线的判定方法——切线的判定定理。
【温馨提示】切线的判定必须同时满足以下两个条件: ①经过半径外端;②垂直于这条半径。缺一不可哟!
切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线。
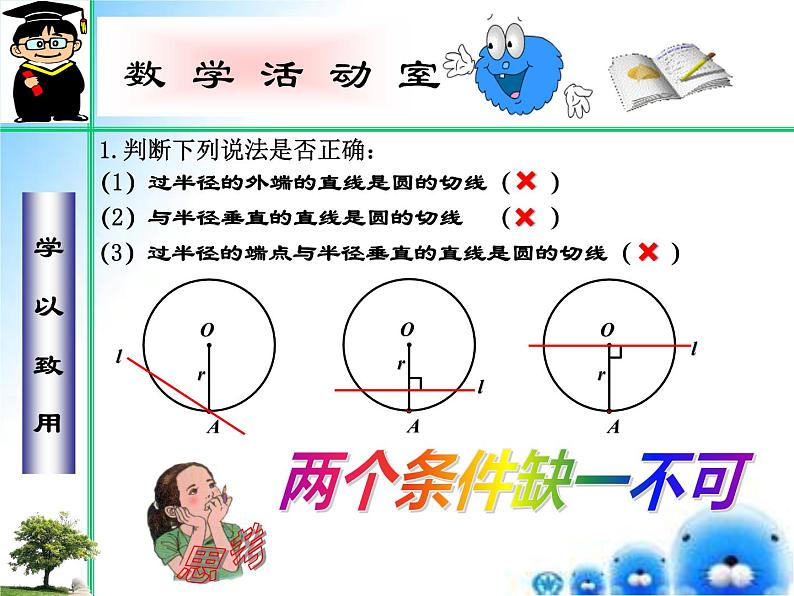
1.判断下列说法是否正确:
(1)过半径的外端的直线是圆的切线( )
(2)与半径垂直的直线是圆的切线 ( )
(3)过半径的端点与半径垂直的直线是圆的切线( )
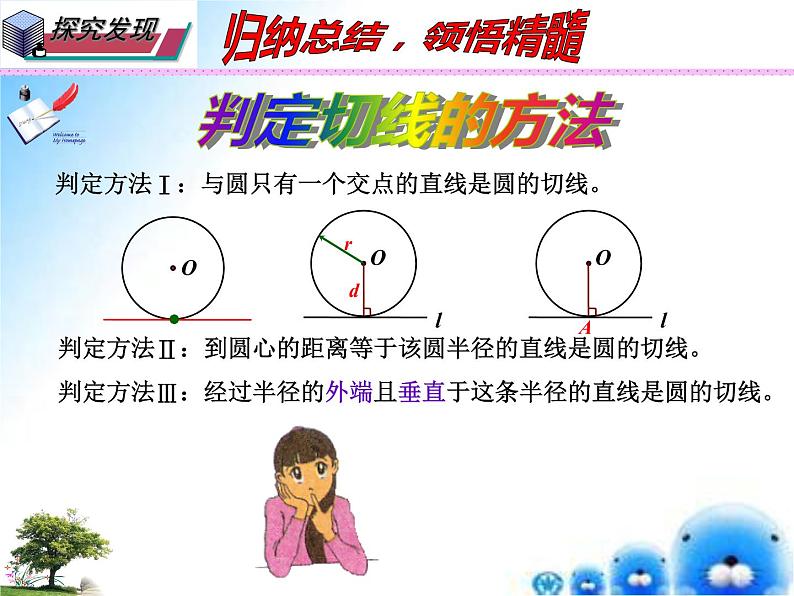
判定方法Ⅰ:与圆只有一个交点的直线是圆的切线。
判定方法Ⅱ:到圆心的距离等于该圆半径的直线是圆的切线。
判定方法Ⅲ:经过半径的外端且垂直于这条半径的直线是圆的切线。
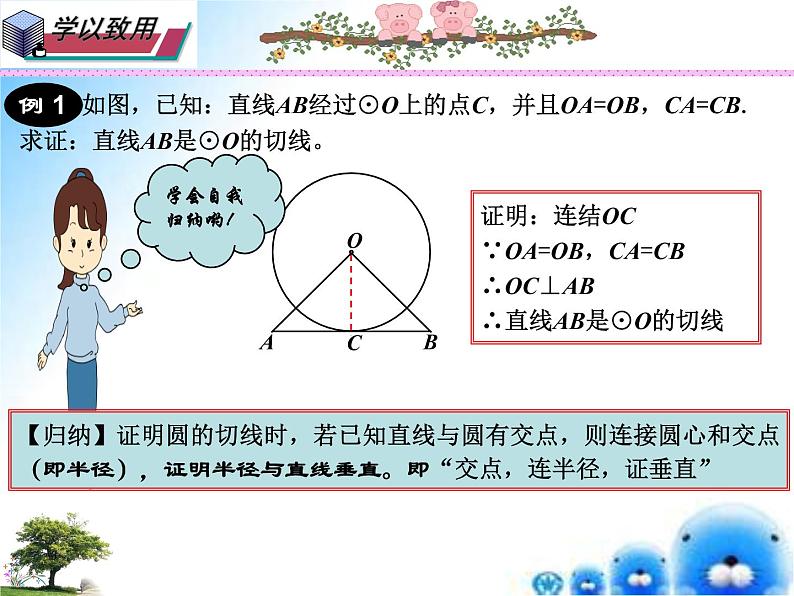
如图,已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线。
证明:连结OC∵OA=OB,CA=CB∴OC⊥AB∴直线AB是⊙O的切线
【归纳】证明圆的切线时,若已知直线与圆有交点,则连接圆心和交点(即半径),证明半径与直线垂直。即“交点,连半径,证垂直”
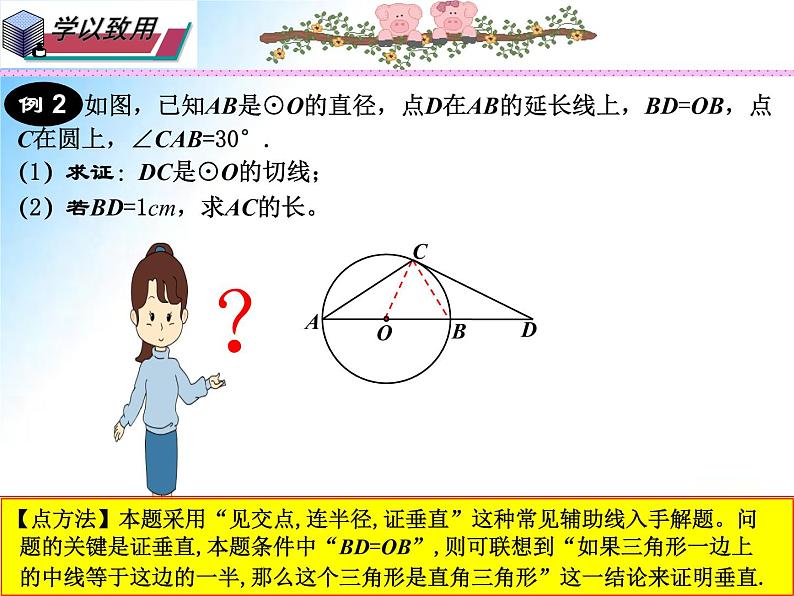
如图,已知AB是⊙O的直径,点D在AB的延长线上,BD=OB,点
C在圆上,∠CAB=30°.
【点方法】本题采用“见交点,连半径,证垂直”这种常见辅助线入手解题。问 题的关键是证垂直,本题条件中“BD=OB”,则可联想到“如果三角形一边上 的中线等于这边的一半,那么这个三角形是直角三角形”这一结论来证明垂直.
(1)求证:DC是⊙O的切线;
(2)若BD=1cm,求AC的长。
如图,在△ABC中,∠CAB=90°,∠CBA=50°,以AB为直径作⊙O
交BC于点D,点E在边AC上,且满足ED=EA.
(2)求证:直线BD与⊙O相切。
【点方法】已知直线与圆的公共点证切线的关键就是证明“半径与直线垂直”. 若已知有90°(直角),则可利用三角形全等进行转化,证明未知的角等于 90°,从而达到证明垂直的目的。
(1)求∠DOA的度数;
3.如图,AB是⊙O的直径,点C在⊙O上,连结BC、AC,过点A 作AB的垂线,过O作BC的平行线,两直线交于点D,连结DC 并延长交AB的延长线于点E.求证:DE是⊙O的切线。
如图,AB是⊙O的直径,AB=4,∠ABC=30°,BC交⊙O 于点D,D是
(2)过点D作DE⊥AC,垂足为E,求证:直线DE是⊙O的切线。
【点方法】已知一条直线与某条直线垂直,要证明另一条直线也与这条直线垂 直,则可证明这两条直线平行。当题目中出现“中点”,可结合圆心是任何直径 的中点,构造中位线,利用中位线定理证明平行,从而达到证明垂直的目的。
4.如图,在△ABC中,AB=AC,点O在边AB上,⊙O过点B且分 别与边AB、BC相交于点D、E,EF⊥AC,垂足为点F. 求证:直线EF是⊙O的切线
如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,以D
为圆心,DB的长为半径作⊙D.求证:AC与⊙ D相切。
【点方法】如果条件中不知道直线与圆是否有公共点,其证法是过圆心作直线 的垂线段,再证明垂线段等于半径的长即可,简记为:作垂线,证半径。
5.如图,AB是⊙O的直径,∠ABT=45°,AT=AB.
(1)求证:AT是⊙O的切线;
(2)连结OT交⊙O于点C,连结AC,求tan∠TAC的值。
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
初中数学华师大版九年级下册第27章 圆27.2 与圆有关的位置关系3. 切线精品课件ppt: 这是一份初中数学华师大版九年级下册<a href="/sx/tb_c21377_t3/?tag_id=26" target="_blank">第27章 圆27.2 与圆有关的位置关系3. 切线精品课件ppt</a>,文件包含2723第1课时切线的判定与性质pptx、2723第1课时反证法wmv等2份课件配套教学资源,其中PPT共38页, 欢迎下载使用。
初中数学华师大版九年级下册3. 切线优秀课件ppt: 这是一份初中数学华师大版九年级下册3. 切线优秀课件ppt,文件包含2723切线2课件pptx、2723切线2教案docx等2份课件配套教学资源,其中PPT共23页, 欢迎下载使用。
初中数学华师大版九年级下册3. 切线一等奖课件ppt: 这是一份初中数学华师大版九年级下册3. 切线一等奖课件ppt,文件包含2723切线1课件pptx、2723切线1教案docx等2份课件配套教学资源,其中PPT共22页, 欢迎下载使用。














