初中北师大版1 认识分式公开课第二课时教学设计

这是一份初中北师大版1 认识分式公开课第二课时教学设计，共4页。教案主要包含了分式的基本性质，分式基本性质的应用等内容，欢迎下载使用。


课题
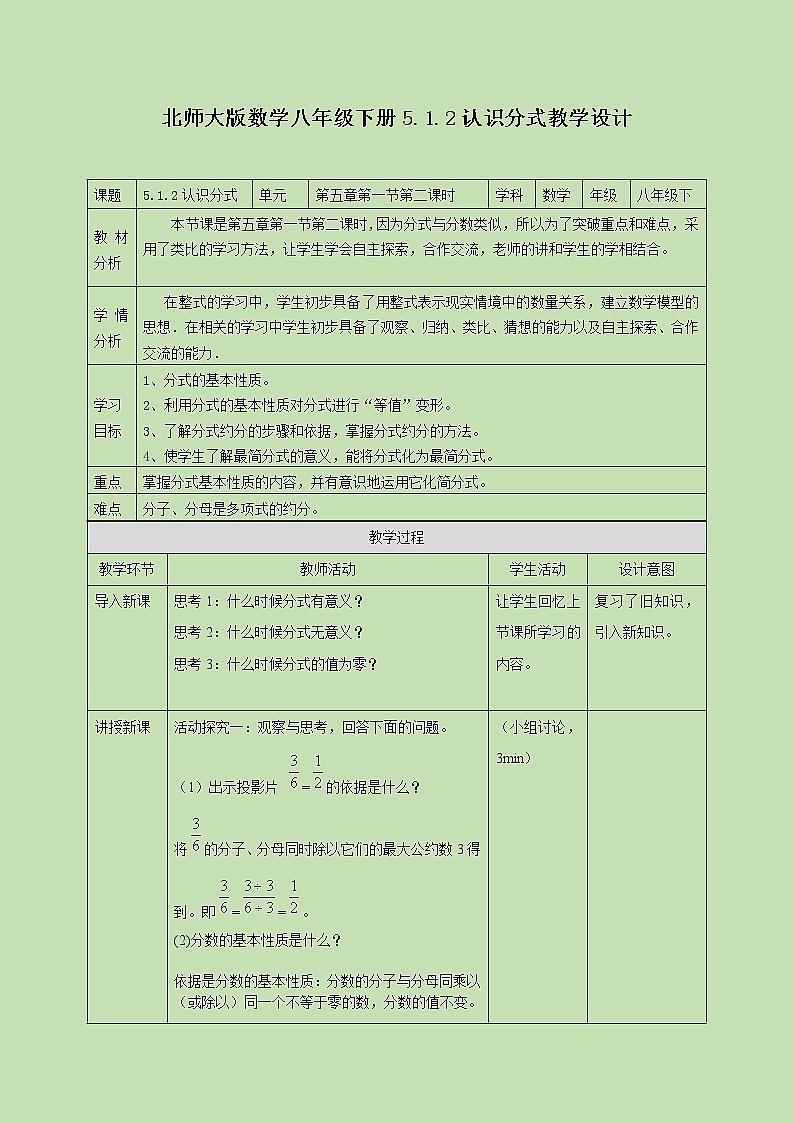
5.1.2认识分式
单元
第五章第一节第二课时
学科
数学
年级
八年级下
教材分析
本节课是第五章第一节第二课时,因为分式与分数类似，所以为了突破重点和难点，采用了类比的学习方法，让学生学会自主探索，合作交流，老师的讲和学生的学相结合。
学情分析
在整式的学习中，学生初步具备了用整式表示现实情境中的数量关系，建立数学模型的思想．在相关的学习中学生初步具备了观察、归纳、类比、猜想的能力以及自主探索、合作交流的能力．
学习
目标
1、分式的基本性质。
2、利用分式的基本性质对分式进行“等值”变形。
3、了解分式约分的步骤和依据，掌握分式约分的方法。
4、使学生了解最简分式的意义，能将分式化为最简分式。
重点
掌握分式基本性质的内容，并有意识地运用它化简分式。
难点
分子、分母是多项式的约分。
教学过程
教学环节
教师活动
学生活动
设计意图
导入新课
思考1：什么时候分式有意义？
思考2：什么时候分式无意义？
思考3：什么时候分式的值为零？
让学生回忆上节课所学习的内容。
复习了旧知识，引入新知识。
讲授新课
活动探究一：观察与思考，回答下面的问题。
（1）出示投影片 =的依据是什么？
将的分子、分母同时除以它们的最大公约数3得到。即==。
(2)分数的基本性质是什么？
依据是分数的基本性质：分数的分子与分母同乘以（或除以）同一个不等于零的数，分数的值不变。
(3)你认为分式与相等吗？与呢？与同伴交流。
分式与相等，在分式中，a≠0，所以==;
分式与也是相等的。在分式中，n≠0，所以==。
例2 下列等式的右边是怎样从左边得到的？
（1）=（y≠0）；（2）=
小结：应用分式的基本性质时，一定要确定分式在有意义的情况下才能应用．应用时要注意是否符合两个“同”：一是要同时作“乘法”或“除法”运算；二是“乘(或除以)”的对象必须是同一个不等于0的整式．
例3 化简下列各式：
（1）;（2）。
活动探究二：观察与思考，回答下面的问题。（小组讨论，3min）
1、约分的依据是什么？
2、当分子、分母是多项式时，约分时应先怎样？
把一个分式的分子和分母的公因式约去，这种变形我们称为分式的约分。
约分的基本步骤：
（１）若分子﹑分母都是单项式，则约简系数，并
（1）;
［师］在刚才化简第（1）题中的分式时，一位同学这样做的
议一议 在化简时，小颖是这样做的：=；小明是这样做的：=
你对他们两人的做法有何看法？与同伴交流。
注意：在化简结果中，分子和分母已没有公因式，这样的分式称为最简分式.化简分式时，通常把结果成为最简分式或整式。
课堂练习：
约分
化简下列分式:
拓展提高：
不改变分式的值，把下列各式的分子与分母中的各项系数化为整数。

作业布置：
已知a-b-3ab=0，求 的值。
（小组讨论，3min）
同学们可以注意到（1）中的分式，分子、分母都是单项式，把公有的因式分离出来，然后利用分式的基本性质，把公因式约去即可，这样的公因式如何分离出来呢？同学们可小组讨论。
独立完成，提问学生回答。
利用分数的基本性质可以对分数进行化简。利用分式的基本性质也可以对分式化简。
化简一个分数，首先找到分子、分母的最大公因数，然后利用分数的基本性质就可将分数化简。
让学生明白，约分过程中，有时还需运用分式的符号法则使最后结果形式简捷；约分的依据是分式的基本性质。
拓展学生的思维，加强学生应对难题的能力。
课堂小结
1﹑分式的基本性质。
2﹑分式基本性质的应用。
3﹑化简分式,通常要使结果成为最简分式或者整式。
（１）若分子﹑分母都是单项式，则约简系数，并约去相同字母的最低次幂；
（２）若分子﹑分母含有多项式，则先将多项式分解因式，然后约去分子﹑分母所有的公因式．
提问学生自己总结。
总结归纳本节课的内容，帮助学生整理思路，消化知识，构造严谨的知识体系。
板书
5.1.2 分式（二）
一、分式的基本性质。
二、分式基本性质的应用。
三、化简分式,通常要使结果成为最简分式或者整式。
例题
随堂练习