








- 湘教版数学七下:第4章 相交线与平行线小结与复习 课件+教案 课件 24 次下载
- 湘教版数学七下:5.1.1 轴对称图形课件+教案 课件 25 次下载
- 湘教版数学七下:5.2 旋转 课件+教案 课件 24 次下载
- 湘教版数学七下:5.3 图形变换的简单应用 课件+教案 课件 22 次下载
- 湘教版数学七下:第5章 轴对称与旋转小结与复习 课件+教案 课件 24 次下载
初中数学湘教版七年级下册5.1.2轴对称变换优质课ppt课件
展开5.1.2 轴对称变换教案
主备人: 审核人: 本章课时序号:2
课 题 | 轴对称变换 | 课型 | 新授课 |
教学目标 | 1. 理解轴对称变换的概念,成轴对称图形的概念; 2. 掌握轴对称变换的性质,成轴对称图形的性质; 3. 能根据要求作出与已知图形成轴对称的图形; 4. 能解答两个图形成轴对称的相关问题; 5. 感受成轴对称图形之美,激发学习数学的兴趣。 | ||
教学重点 | 1. 轴对称变换、成轴对称图形的概念; 2. 轴对称变换的性质,成轴对称图形的性质。 | ||
教学难点 | 1. 用轴对称变换的性质和成轴对称图形的性质解决问题。 2. 作出一个图形关于已知直线成轴对称的图形。 | ||
教 学 活 动 | |||
一、情景导入 复习提问: 如图,右边的图案是由左边的图形经过怎样的图形变换得到的?这种图形变换有什么性质?
生1:右边的图案是由左边的图形经过连续几次平移得到的。 生2:平移不改变图形的形状和大小,不改变直线的方向。 生3:一个图形和它经过平移所得的图形中,两组对应点的连线平行(或共线)且相等。 提出新问题,导入新课: 下图中左边的头像,经过变换可以得到右边的头像。这是一种怎样的图形变换呢?这种变换有哪些性质?
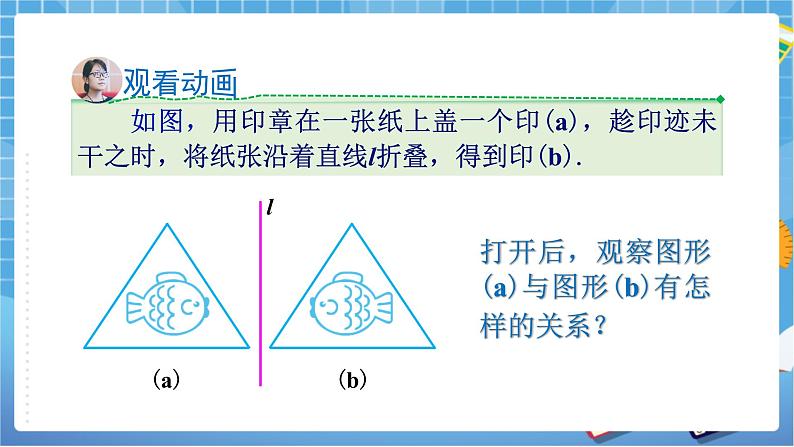
二、教学新知 (一)讲解轴对称变换的概念 1、 观看动画: 如图,用印章在一张纸上盖一个印(a),趁印迹未干之时,将纸张沿着直线l折叠,得到印(b). (1)教师播放动画,学生观看; (2)提问:打开后,观察图形(a)与图形(b)有怎样的关系? 生:将图形(a)沿直线l翻折,便可“复制”出图形(b). 2、 抽象概念: (1)轴对称变换:把图形(a)沿着直线l翻折并将图形“复印”下来得到图形(b),就叫做该图形关于直线l作了轴对称变换,也叫轴反射.图形(a)叫做原像,图形(b)叫做图形(a)在这个反射下的像. (2)如果一个图形关于某一条直线作轴对称变换后,能够与另一个图形重合,那么就说这两个图形关于这条直线对称,也称这两个图形成轴对称.这条直线叫做对称轴. (3)原像与像中能互相重合的两个点,其中一点叫做另一个点的对应点.例如,图中,点A′叫做点A的对应点. (二)探究轴对称变换的性质 1、 出示问题: 如图,三角形ABC和三角形A′B′C′关于直线l成轴对称,点P和P′是对应点,线段PP′交直线l于点D.那么线段PP′与对称轴l有什么关系呢? 2、 学生讨论后,教师启发: 因为三角形ABC和三角形A′B′C′关于直线l成轴对称,将上图沿直线l折叠,则点P与P′重合,所以PD与P′D,∠1与∠2也重合.故有PD=P′D,∠1=∠2=90°.即直线l垂直平分线段PP′. 3、 归纳性质,并用ppt展示: 成轴对称图形的性质: 成轴对称的两个图形,对应点的连线被对称轴垂直平分。 4、 教师指出:反过来,如果两个图形的对应点的连线被同一条直线垂直平分,那么这 两个图形关于这条直线对称. 三、教学例题 (一)教学例1 例1 如图,已知直线l及直线外一点P,求作点P′,使它与点P关于直线l对称. 1、 讨论作法:因为成轴对称的两个图形,对应点的连线被对称轴垂直平分。因此需作 出直线l的垂线,并在直线l两侧的垂线上截取相等的线段。 2、 教师用动画展示作图过程,学生观看。 3、 用ppt展示作法: 作法: 1. 过点P作PQ⊥l,交l于点O. 2. 在直线PQ上,截取OP′=OP. 则点P′即为所求作的点. 4、 做一做:如图,已知线段AB和直线l,作出与线段AB关于直线l对称的图形. (1)引导学生说出作法:先作出线段两个端点的对应点A′,B′,再连接A′B′。 (2)学生作图,教师巡视,发现问题及时纠正。 (二) 教学例2 例2 如图,已知三角形ABC和直线l,作出与三角形ABC关于直线l对称的图形. 1、 分析:要作三角形ABC关于直线l的对称图形,只要作出三角形的顶点A,B,C关于直线l的对应点A′,B′,C′. 连接这些对应点,得到的三角形A′B′C′,就是三角形ABC关于直线l对称的图形. 2、 教师用动画展示作图过程,学生观看。 3、 用ppt展示作法: 作法: 1. 过点A作直线l的垂线,垂足为点O,在垂线上截取OA′=OA,点A′就是点A关于直线l的对称点. 2. 类似地,分别作出点B,C关于直线l的对称点B′,C′. 3. 连接A′B′,B′C′,C′A′得到三角形A′B′C′即为所求。 4、 小结作法:根据成轴对称图形的性质,先作出图形的关键对应点,再连线成图。 四、课堂练习 (一)巩固练习 1、 课后练习第2题。 学生回答都成轴对称,画出对称轴,标出一对对应点。教师巡视指导。 2、 习题5.1第3题。 学生回答:蓝色的三角形与三角形2、3、4成轴对称.整个图形是轴对称图形.共有4条对称轴. 3、 习题5.1第5题。 (1)学生交流讨论解法(注意说清解法依据) (2)教师展示解答过程: 解:因为三角形ABC和三角形A′B′C′关于直线l对称,所以∠A′B′C′=∠ABC=90°.三角形A′B′C′的周长=三角形ABC的周长=3+4+5=9 (二)能力提升 4、 如图,将△ABC沿直线DE折叠,使点B与点A重合,已知AC=5,BC=17,则△ADC的周长为( ) A. 12 B. 17 C. 22 D. 27 【答案】C 【解析】叠就是作轴对称变换,因此AD=BD,△ADC的周长=AD+DC+AC=BD+DC+AC=BC+AC =17+5=22. 5、 如图,将△ABC沿直线AF作轴对称变换,得到△ADE.已知∠BAE=25°,∠CAF=17.5°. (1)求∠BAC的度数; (2)当∠B是多少度时,AD⊥DE? 【解析】(1)根据轴对称变换的性质得∠EAF=∠CAF=17.5°,所以∠BAC=∠BAE+2∠CAF=25°+2×17.5°=60°. (2)∵AD⊥DE,∴∠AED=90°,∴∠ACB=90°. 在△ABC中,由三角形的内角和性质可得∠B=30°. 四、课堂总结 1、 什么是轴对称变换? 学生回答后用ppt展示: 把图形(a)沿着直线l翻折并将图形“复印”下来得到图形(b),就叫做该图形关于直线l作了轴对称变换。. 2、 轴对称变换有什么性质? 学生回答后用ppt展示: (1)轴对称变换不改变图形的形状和大小. (2)即:图形经过轴对称变换,长度、角度和面积等都不改变. 3、 关于直线成轴对称的图形有什么性质? 学生回答后用ppt展示: (1)成轴对称的两个图形,对应点的连线被对称轴垂直平分. (2)反过来,如果两个图形的对应点的连线被同一条直线垂直平分,那么这两个图形关于这条直线对称. 五、作业布置 1、 以树干为对称轴,画出树的另一半(习题5.1第4题) 2、 用轴对称变换设计服装.(习题5.1第6题) 3、 找生活中成轴对称的实例. | |||
板书设计 | 5.1.2 轴对称变换 1、 轴对称变换的概念; 2、 轴对称变换的性质; 3、 成轴对称图形的概念; 4、 成轴对称图形的性质; 5、 用轴对称变换的方法作成轴对称的图形。 | ||
湘教版七年级下册5.1.2轴对称变换图片ppt课件: 这是一份湘教版七年级下册<a href="/sx/tb_c95292_t3/?tag_id=26" target="_blank">5.1.2轴对称变换图片ppt课件</a>,共27页。PPT课件主要包含了作轴对称图形的方法,∠O′A′B′,A′B′,B′C′,∠A′B′C′,轴对称的性质,轴对称变换,作图方法等内容,欢迎下载使用。
数学七年级下册5.1.2轴对称变换课堂教学课件ppt: 这是一份数学七年级下册5.1.2轴对称变换课堂教学课件ppt,文件包含512轴对称变换课件pptx、512轴对称变换练习doc、512轴对称变换教案doc、512轴对称变换学案doc等4份课件配套教学资源,其中PPT共22页, 欢迎下载使用。
数学七年级下册5.1.2轴对称变换课文内容ppt课件: 这是一份数学七年级下册5.1.2轴对称变换课文内容ppt课件,文件包含512轴对称变换课件ppt、512轴对称变换教案DOCX等2份课件配套教学资源,其中PPT共18页, 欢迎下载使用。













