


初中第1章 直角三角形1.3 直角三角形全等的判定图文ppt课件
展开判定两个三角形全等有哪些方法?有两边和其中一边的对角对应相等的两个三角形是否全等?
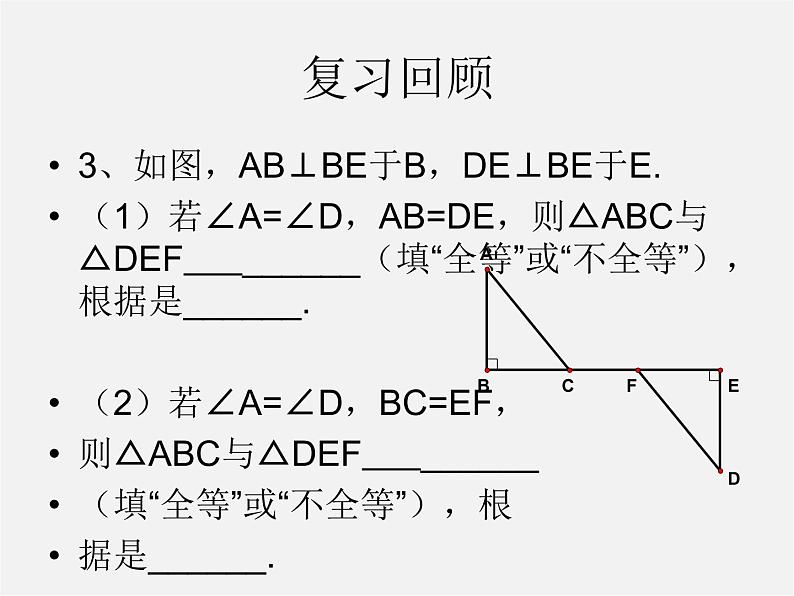
3、如图,AB⊥BE于B,DE⊥BE于E.(1)若∠A=∠D,AB=DE,则△ABC与△DEF ______(填“全等”或“不全等”),根据是______.(2)若∠A=∠D,BC=EF,则△ABC与△DEF ______(填“全等”或“不全等”),根据是______.
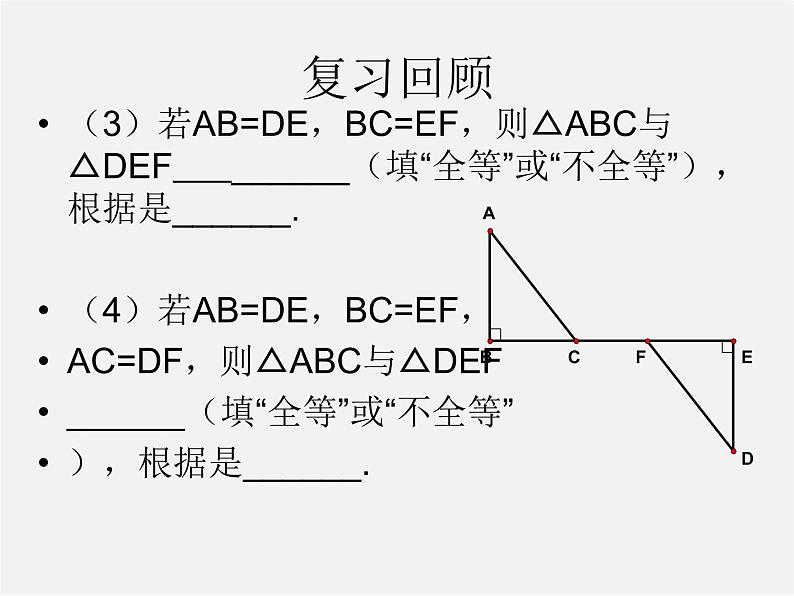
(3)若AB=DE,BC=EF,则△ABC与△DEF ______(填“全等”或“不全等”),根据是______.(4)若AB=DE,BC=EF,AC=DF,则△ABC与△DEF______(填“全等”或“不全等”),根据是______.
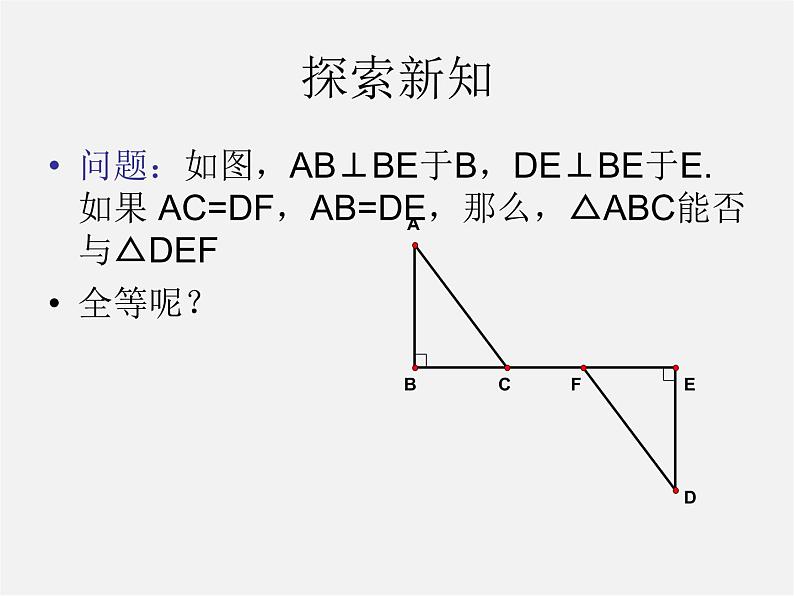
问题:如图,AB⊥BE于B,DE⊥BE于E. 如果 AC=DF,AB=DE,那么,△ABC能否与△DEF全等呢?
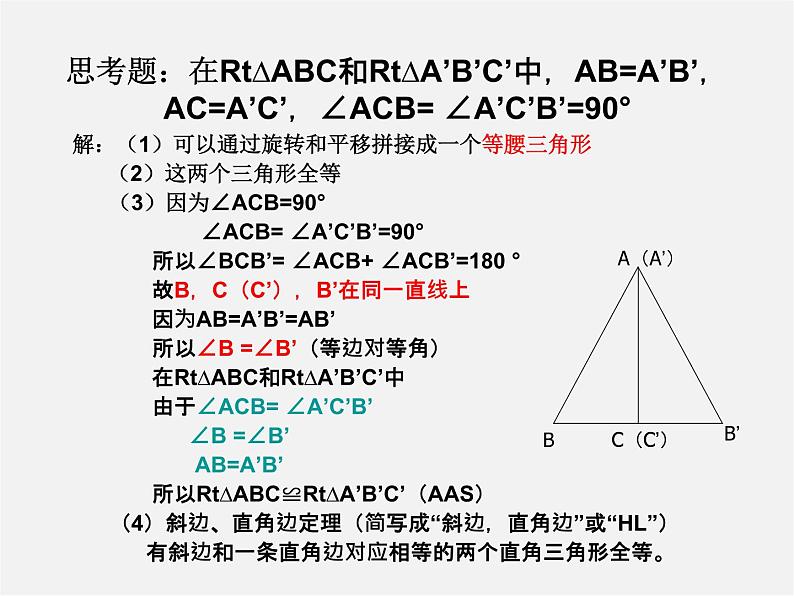
思考题:在Rt∆ABC和Rt∆A’B’C’中,AB=A’B’,AC=A’C’,∠ACB= ∠A’C’B’=90°
你能把这两个三角形通过平移、旋转或轴反射等变换拼接成一个等腰三角形吗?从上面(1)的操作中,你能猜测这两个直角三角形全等吗?请用推理的方法说明你猜想的正确性。你能用语言概括上面发现的结论吗?
解:(1)可以通过旋转和平移拼接成一个等腰三角形 (2)这两个三角形全等 (3)因为∠ACB=90° ∠ACB= ∠A’C’B’=90° 所以∠BCB’= ∠ACB+ ∠ACB’=180 ° 故B,C(C’),B’在同一直线上 因为AB=A’B’=AB’ 所以∠B =∠B’(等边对等角) 在Rt∆ABC和Rt∆A’B’C’中 由于∠ACB= ∠A’C’B’ ∠B =∠B’ AB=A’B’ 所以Rt∆ABC≌Rt∆A’B’C’(AAS) (4)斜边、直角边定理(简写成“斜边,直角边”或“HL”) 有斜边和一条直角边对应相等的两个直角三角形全等。
直角三角形全等的判定定理
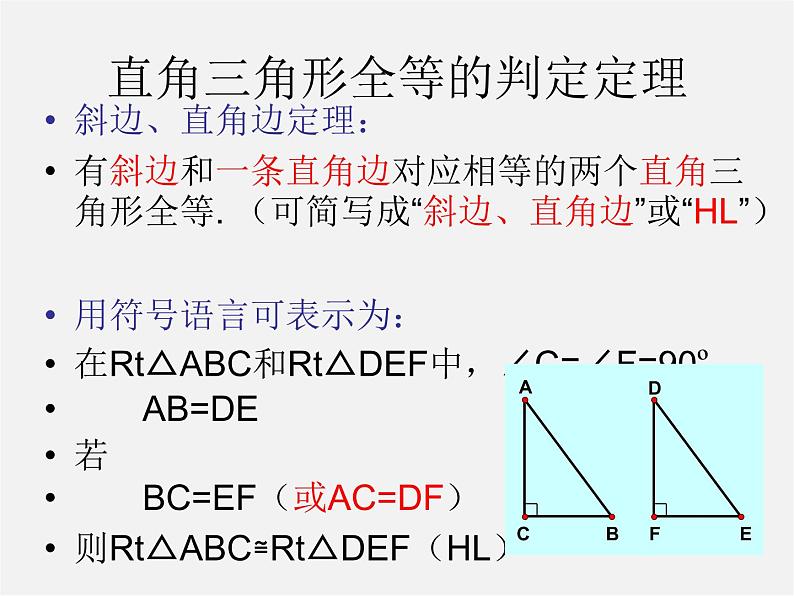
斜边、直角边定理:有斜边和一条直角边对应相等的两个直角三角形全等. (可简写成“斜边、直角边”或“HL”)用符号语言可表示为:在Rt△ABC和Rt△DEF中,∠C=∠F=90º, AB=DE若 BC=EF(或AC=DF)则Rt△ABC≌Rt△DEF(HL)
例1、如图,∠AOB内部有一条射线OC,P是OC上一点,PD⊥OA于D,PE⊥OB于E,且PD=PE.求证:OP平分∠AOB.证明:∵PD⊥OA,PE⊥OB∴△PEO和△PDO是Rt△.在Rt△PEO和Rt△PDO中, OP=OP (公共边) PD=PE (已知)∴Rt△PEO≌Rt△PDO(HL)∴∠AOC=∠BOC,即:OP平分∠AOB.
1、如图,AC⊥CB,BD⊥BC,AB=DC,AB与CD平行吗?为什么?
2、如图, AC与BD交于点O, 且AC=BD, AD⊥AC, BC⊥BD.求证:DO=CO.
3、如图,∠ABD=∠ACD=90º,∠1=∠2,则AD平分∠BAC. 请说明理由.
4、判断题:(对的打“T”,错的打“F”)(1)两条直角边分别相等的两个直角三角形全等. ( )(2)有一角和一斜边分别相等的两个直角三角形全等. ( )(3)有一边相等的两等腰直角三角形全等.( )(4)一锐角和斜边对应相等的两个直角三角形全等. ( )(5)斜边和一条直角边对应相等的两个直角三角形全等. ( )
1、判定直角三角形全等的特殊判定“HL”定理:有斜边和一条直角边对应相等的两个直角三角形全等. (可简写成“斜边、直角边”或“HL”)2、角平分线定理的逆定理:到一个角两边的距离相等的点在这个角的角平分线上.3、直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法: SAS、ASA、AAS、SSS,还有直角三角形特殊的判定方法——“HL”.
已知:如图,在△ABC和△DEF中,AP、DQ分别是高,并且AB=DE,AP=DQ,∠BAC=∠EDF,求证:△ABC≌△DEF
∠BAC=∠EDF, AB=DE,∠B=∠E
分析: △ABC≌△DEF
Rt△ABP≌Rt△DEQ
AB=DE,AP=DQ
已知AB//CD, ∠A=90 °、AB=CE、BC=DE,试问DE与BC的位置关系是怎样的?
解:因为AB//CD, ∠A=90 ° 所以∠DCA=180 °- ∠A=90 °(两直线平行,同旁内角互补) 在Rt∆ABC和Rt∆CED中, 因为AB=CE BC=DE 所以Rt∆ABC≌Rt∆CED(HL) 所以∠1= ∠D(全等三角形对应角相等) ∠1+ ∠2= ∠2+ ∠D=90° (直角三角形两锐角互余)(或者∠2= ∠B,得到∠1+ ∠2= ∠1+ ∠B=90°) 因此∠EMC=90° 即DE⊥BC
4、如图,已知A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC,连结BD交AC于M,若AB=CD,试说明AC与BD互相平分.
初中数学湘教版八年级下册2.7 正方形教案配套ppt课件: 这是一份初中数学湘教版八年级下册2.7 正方形教案配套ppt课件,共24页。PPT课件主要包含了可以知道,∵DF⊥DE,∴∠1∠2等内容,欢迎下载使用。
初中数学湘教版八年级下册1.3 直角三角形全等的判定图文ppt课件: 这是一份初中数学湘教版八年级下册1.3 直角三角形全等的判定图文ppt课件,共11页。PPT课件主要包含了图1-22,图1-23,图1-24,图1-25,连接AB,答不对等内容,欢迎下载使用。
初中湘教版1.3 直角三角形全等的判定教案配套课件ppt: 这是一份初中湘教版1.3 直角三角形全等的判定教案配套课件ppt,共27页。PPT课件主要包含了忆一忆,想一想,动动手做一做,你发现了什么,直角边公理,条件1,条件2,SSS,小试牛刀,解BDCD等内容,欢迎下载使用。













