2021学年第十一章 三角形11.2 与三角形有关的角11.2.1 三角形的内角教学演示课件ppt

这是一份2021学年第十一章 三角形11.2 与三角形有关的角11.2.1 三角形的内角教学演示课件ppt，共18页。

同学们，你们知道其中的道理吗？
一天，三角形蓝和三角形红见面了
红不服气的说：“那可不好说噢，你自己量量看！”
蓝用量角器量了量自己和红的三个内角，就不再说话了！
1.情境激趣 引出课题
蓝炫耀的说：“我的个子比你大，所以我的内角和比你大！”
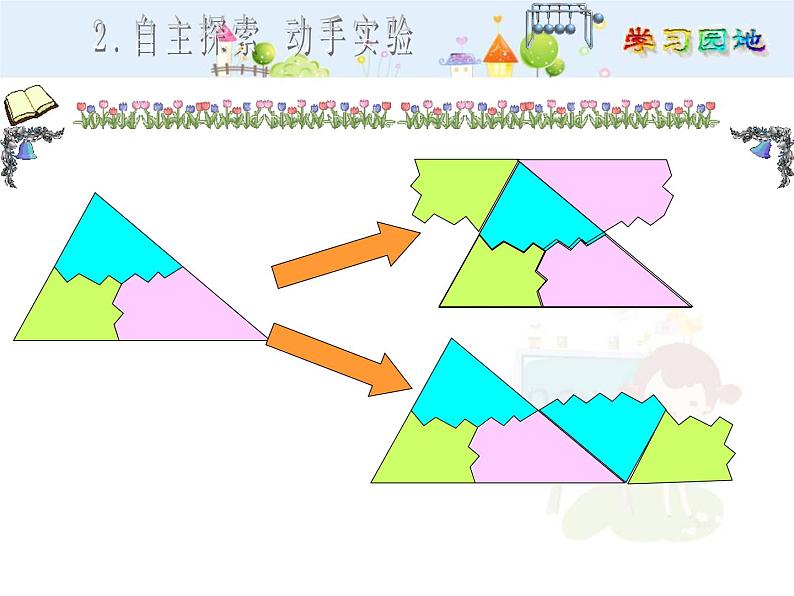
三角形的三个内角和是180°，你是怎样得知的？
2.自主探索 动手实验
拿出三角形，将它的两个内角撕下，把三个内角拼合在一起看看，你能量得它们的和为180°吗？
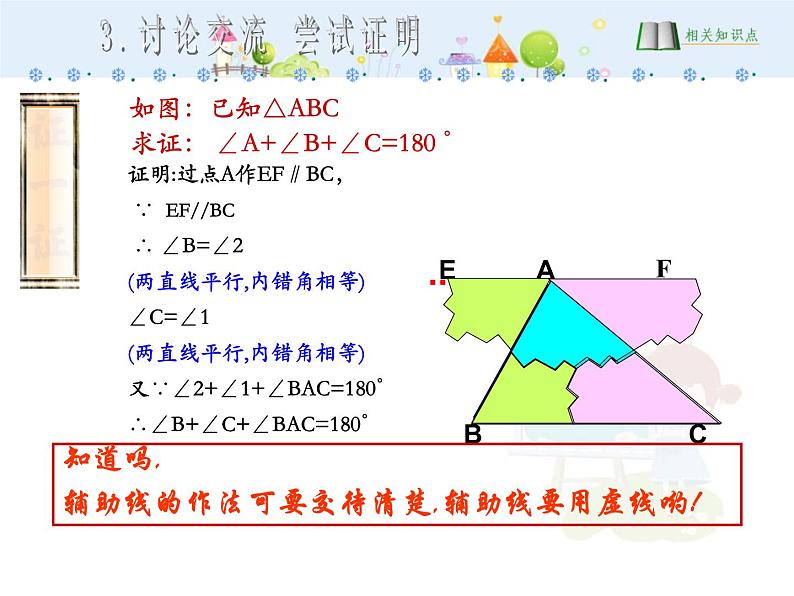
如图：已知△ABC 求证： ∠A+∠B+∠C=180 °
证明:过点A作EF∥BC， ∵ EF//BC ∴ ∠B=∠2(两直线平行,内错角相等) ∠C=∠1(两直线平行,内错角相等) 又∵∠2+∠1+∠BAC=180°∴∠B+∠C+∠BAC=180°
知道吗, 辅助线的作法可要交待清楚,辅助线要用虚线哟!
3.讨论交流 尝试证明
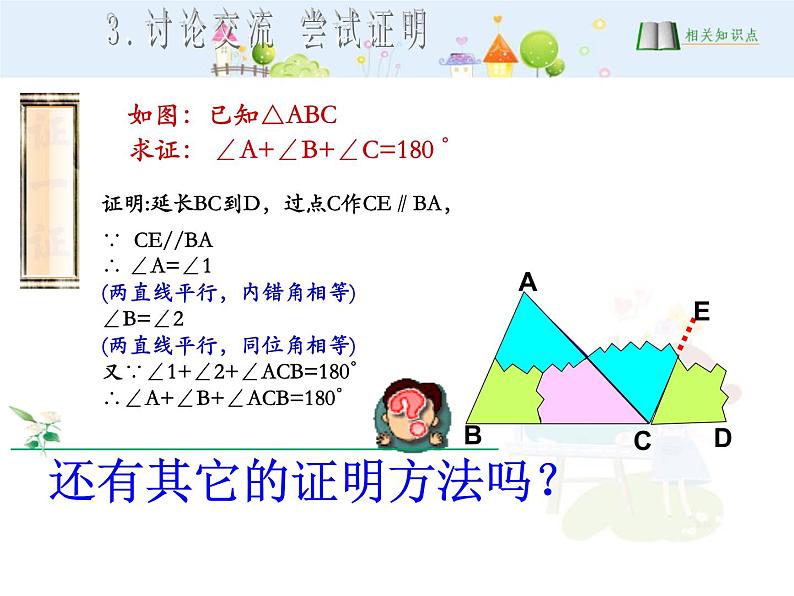
证明:延长BC到D，过点C作CE∥BA，∵ CE//BA∴ ∠A=∠1 (两直线平行，内错角相等)∠B=∠2(两直线平行，同位角相等)又∵∠1+∠2+∠ACB=180°∴∠A+∠B+∠ACB=180°
还有其它的证明方法吗？
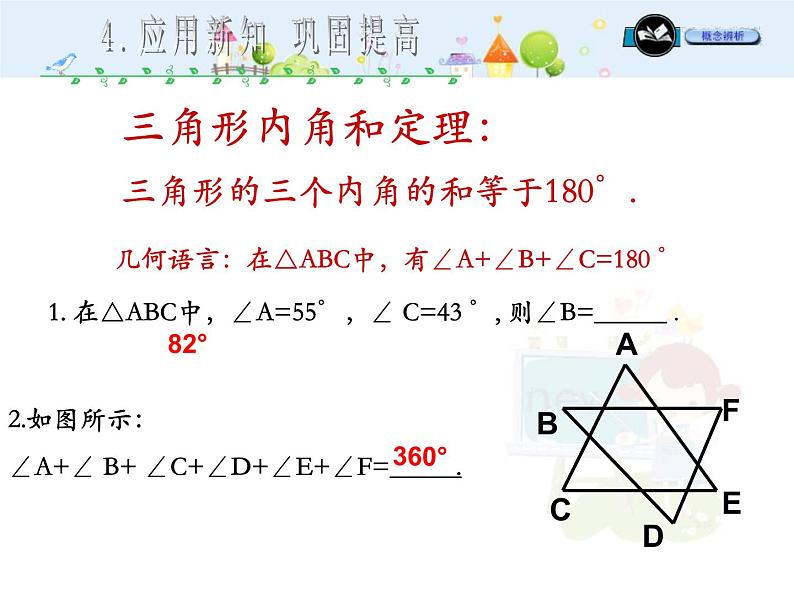
三角形内角和定理：三角形的三个内角的和等于180°.
几何语言：在△ABC中，有∠A+∠B+∠C=180 °
1. 在△ABC中，∠A=55°，∠ C=43 °, 则∠B= .
2.如图所示：∠A+∠ B+ ∠C+∠D+∠E+∠F= .
4.应用新知 巩固提高
例1：如图，在△ ABC中， ∠ BAC=40°， ∠ B=75 ° ，AD是△ ABC 的角平分线，求∠ ADB的度数。
解：由∠ BAC=40°AD是角平分线得∠BAD=20 ° 在△ ABD中， ∠ ADB=180 °--∠B--∠BAD =180°--75°--20° =85°
例2：如图，C岛在A岛的北偏东50°方向，B岛在A岛的北偏东80 °方向，C岛在B岛的北偏西40 °方向。从C岛看A、B两岛的视角∠ACB是多少度？
解：由题意得∠DAC=50° ∠DAB= 80° ∠CBE=40°
∴∠CAB=∠DAB- ∠CAB = 80°- 50°=30°
又∵AD//BE∴∠DAB+∠ABE=180° ∴∠ABE =180°-∠DAB = 180°-80°=100°
∴∠ABC=∠ABE- ∠CBE =100°- 40°=60°
∴在△ABC中，∠ACB=180°-∠CAB- ∠CBA =180°- 30°-60° =90°
在△ABC中， ∠A :∠B:∠C=1:2:3，则△ABC的形状是_________.
下列说法中正确的是（ ）A三角形的内角中最多有2个锐角B三角形的内角中最多有2个钝角C三角形的内角中最多有1个直角D三角形的内角都大于60°
如图∠1+∠ 2+ ∠ 3+∠4=___________ 。
如图AD//BC，CE⊥AB，垂足为E，∠A= 125°则∠BCE 的度数是_________.
6.畅谈体会 课外延伸
1、通过本节课学习，你有哪些收获？
（1）如图，在△ABC中，∠ABC和∠ACB的角平分线相交 于点O，若∠A=70°，求∠BOC的度数。
（2）把（1）中的∠A=70°这个条件去掉，试探索∠BOC和 ∠A之间有怎样的数量关系。