初中数学人教版九年级上册24.2.2 直线和圆的位置关系教课ppt课件

这是一份初中数学人教版九年级上册24.2.2 直线和圆的位置关系教课ppt课件，共17页。PPT课件主要包含了两个条件缺一不可等内容，欢迎下载使用。

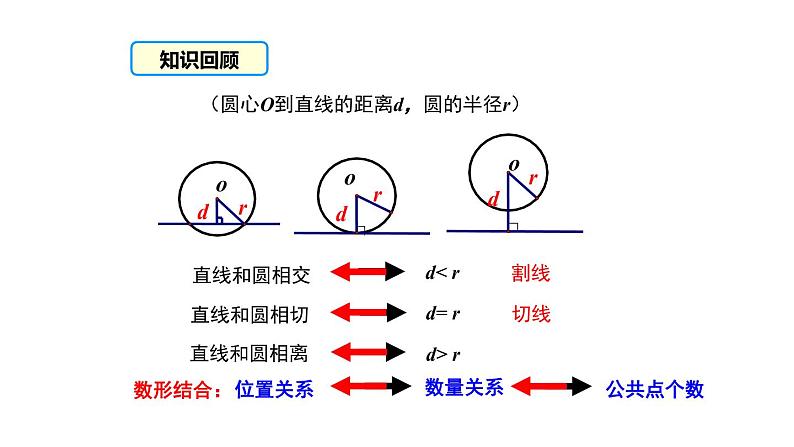
（圆心O到直线的距离d，圆的半径r）
在⊙O中,经过半径OA的外端点A作直线BC⊥OA,则圆心O到直线BC的距离是多少?______,直线BC和⊙O有什么位置关系?_________.
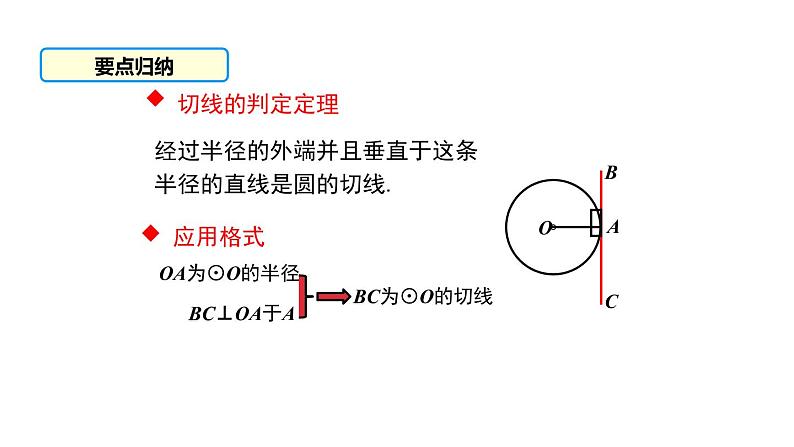
∵ OA 为⊙O的半径 且OA⊥BC,
∴ BC为⊙O的切线.
经过半径的外端并且垂直于这条半径的直线是圆的切线.
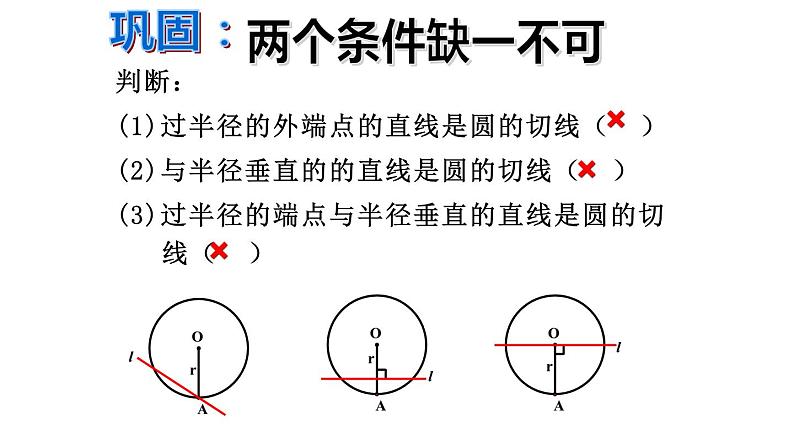
判断：(1)过半径的外端点的直线是圆的切线（ ）(2)与半径垂直的的直线是圆的切线（ ）(3)过半径的端点与半径垂直的直线是圆的切线（ ）
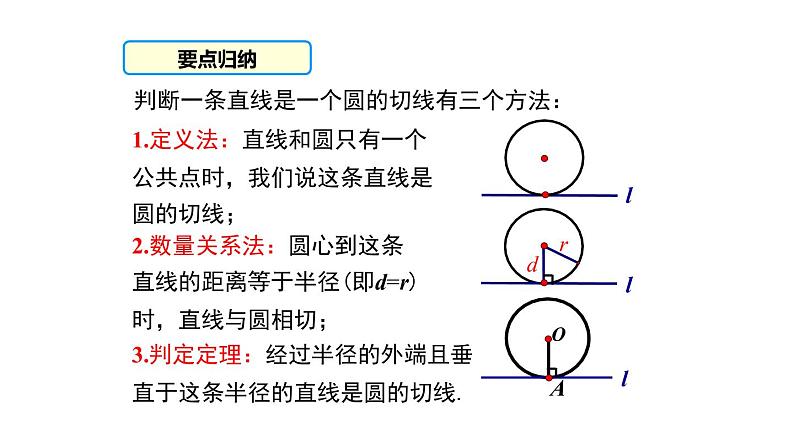
判断一条直线是一个圆的切线有三个方法：
1.定义法：直线和圆只有一个公共点时，我们说这条直线是圆的切线；
2.数量关系法：圆心到这条直线的距离等于半径(即d=r)时，直线与圆相切；
3.判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线.
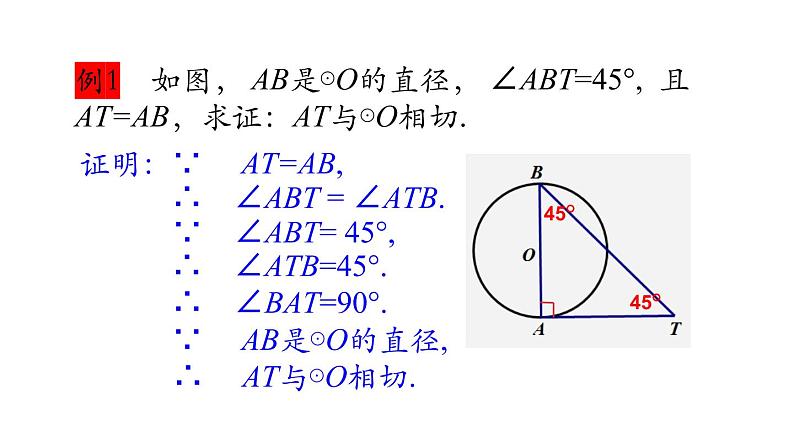
例1 如图， AB是⊙O的直径， ∠ABT=45°, 且AT=AB，求证：AT与⊙O相切.
证明：∵ AT=AB,
∴ ∠ABT = ∠ATB.
∵ ∠ABT= 45°,
∴ ∠ATB=45°.
∴ ∠BAT=90°.
∵ AB是⊙O的直径,
∴ AT与⊙O相切.
例2.直线AB经过⊙O上的点C,并且OA=OB,CA=CB.求证:直线AB是⊙O的切线.
分析：由于AB过⊙O上的点C，所以连接OC，只要证明AB⊥OC即可。
有交点，连半径，证垂直
1、如图，线段AB经过圆心O，交⊙O于点A、C，∠BAD＝∠B＝30°，BD交圆于点D。求证：BD是⊙O的切线。
∴直线BD是⊙O的切线
∵ ∠BOD＝2∠BAD＝60°
∴∠BDO＝180°－∠B－∠BOD＝90°
例3、如图,△ABC中,AB=AC,O是底边BC中点，腰AB与⊙O相切于D点，求证：AC是⊙O 的切线.
无交点，作垂直，证半径
2、 如图，在Rt△ABC 中，∠ABC =90°，∠BAC的平分线交BC于D，以D为圆心，DB长为半径作⊙D．求证：AC 是⊙O 的切线．
1.定义法:和圆有且只有一个公共点的直线是圆的切线.2.数量法(d=r):和圆心距离等于半径的直线是圆的切线.3.判定定理:经过半径外端且垂直于这条半径的直线是 圆的切线.
证明直线与圆相切有如下三种途径:
即 证切线时常用辅助线添加方法： ①有交点，连半径，证垂直；②无交点，作垂直，证半径.
如果l是⊙O的切线,切点为A,那么半径OA与直线l是不是一定垂直呢?
圆的切线垂直于过切点的半径
例4 如图，PA是⊙O的切线，切点为A，PO的延长线交⊙O于点B，连接AB.若∠B=25°，求∠P的度数.
∵∠AOP=2∠B=50°，
∴∠P=180°-90°-50°=40°.
见切线，连切点，得垂直
4.如图，在⊙O的内接四边形ABCD中，AB是直径，∠BCD=120°，过D点的切线PD与直线AB交于点P，则∠ADP的度数为（ ）A．40° B．35° C．30° D．45°
3.如图所示，A是⊙O上一点，且AO=5,PO=13,AP=12,则PA与⊙O的位置关系是 .
练一练