初中数学人教版七年级下册9.3 一元一次不等式组课时训练

这是一份初中数学人教版七年级下册9.3 一元一次不等式组课时训练，共7页。试卷主要包含了知识点，考点点拨与训练等内容，欢迎下载使用。
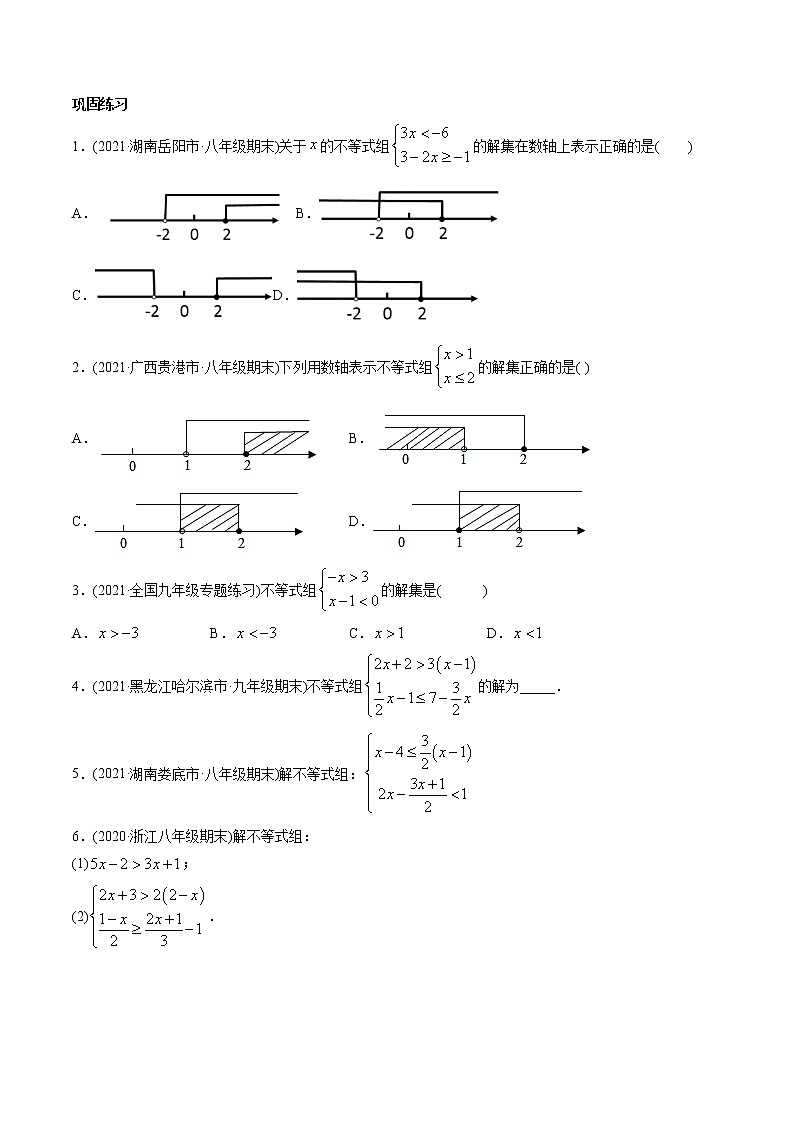
专题9.3一元一次不等式组典例体系(本专题共35题19页) 一、知识点1、不等式组中含有一个未知数，并且所含未知数的项的次数都是1，这样的不等式组叫一元一次不等式组。使不等式组中的每个不等式都成立的未知数的值叫不等式组的解，一个不等式组的所有的解组成的集合，叫这个不等式组的解集解(简称不等式组的解)。不等式组的解集可以在数轴上表示出来。求不等式组的解集的过程叫解不等式组。2、、解一元一次不等式组的一般步骤：①求出这个不等式组中各个不等式的解集；②利用数轴求出这些不等式的解集的公共部分，得到这个不等式组的解集。如果这些不等式的解集的没有公共部分，则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )。3、确定不等式组的解的口诀：大大取大，小小取小，大小小大取中间，大大小小无处找。二、考点点拨与训练考点1：解一元一次不等式组典例：(2020·浙江八年级期末)解不等式组，并把不等式组的解在数轴上表示出来．方法或规律点拨本题考查了不等式组的解法，用数轴表示不等式的解集时，要注意“两定”：一是定界点，一般在数轴上只标出原点和界点即可．定边界点时要注意，点是实心还是空心，若边界点含于解集为实心点，不含于解集即为空心点；二是定方向，定方向的原则是：“小于向左，大于向右”．巩固练习1．(2021·湖南岳阳市·八年级期末)关于的不等式组的解集在数轴上表示正确的是(    )A．B．
C．D．
2．(2021·广西贵港市·八年级期末)下列用数轴表示不等式组的解集正确的是( )A． B．C． D．3．(2021·全国九年级专题练习)不等式组的解集是(　　　)A． B． C． D．4．(2021·黑龙江哈尔滨市·九年级期末)不等式组的解为_____．5．(2021·湖南娄底市·八年级期末)解不等式组：6．(2020·浙江八年级期末)解不等式组：(1)；(2)．7．(2021·浙江金华市·八年级期末)解不等式组．8．(2021·浙江绍兴市·八年级期末)解下列一元一次不等式组．9．(2021·湖南怀化市·八年级期末)解不等式(或组)：(1)(2)10．(2021·浙江杭州市·八年级期末)解关于x的不等式组：考点2：求不等式组的整数解典例：(2021·湖南怀化市·八年级期末)已知不等式组．(1)解这个不等式组，并把它的解集在数轴上表示出来．(2)若是这个不等式组的最小整数解，求的值．方法或规律点拨本题主要考查了一元一次不等式组的求解，结合代数式求值是解题的关键．巩固练习1．(2020·浙江杭州市·九年级期末)不等式组的最大整数解为__________．2．(2021·贵州铜仁市·八年级期末)不等式组的正整数解是______．3．(2020·浙江嘉兴市·八年级期末)不等式组的整数解为____________．4．(2021·辽宁本溪市·九年级期末)不等式组的整数解是_________．6．(2021·浙江宁波市·八年级期末)解下面一元一次不等式组，并写出它的所有非负整数解．．7．(2021·湖南岳阳市·八年级期末)解不等式组：，并写出它的所有非负整数解．9．(2021·全国七年级)解不等式组：，并求出最小整数解与最大整数解的和．考点3：列一元一次不等式组典例：试写出一个不等式，使它的解集满足下列条件：(1)不等式的正整数解只有1，2，3；(2)不等式的整数解只有－2，－1，0，1．巩固练习1．(2020·浙江杭州市·九年级一模)为了治理环境，九年级部分同学去植树，若每人平均植树7棵，还剩9棵；若每人平均植树9棵．则有1名同学植树的棵树小于8棵．若设同学人数为x人，下列各项能准确的求出同学人数与种植的树木的数量的是(    )A．7x+9﹣9(x﹣1)＞0 B．7x+9﹣9(x﹣1)＜8C． D．2．(2019·浙江杭州市·八年级期末)小明要制作一个长方形的相片框架，这个框架的长为，面积不小于，则宽的长度应满足的不等式组为(    )A． B． C． D．3．(2020·临沂商城实验学校七年级期末)某种商品的进价为80元，出售时标价为120元，后来由于该商品积压，商店准备打折出售，但要保证利润率不低于5%，则至多可打几折？如果将该商品打x折销售，则下列不等式中能正确表示该商店的促销方式的是(　　)A．120x≥80×5% B．120x﹣80≥80×5%C．120×≥80×5% D．120×﹣80≥80×5%4．(2019·赤壁市神山中学七年级期末)七年级某班部分学生植树，若每人平均植树8棵，还剩7棵；若每人植树9棵，则有一名学生植树的棵树多于3棵而小于6棵．若设学生人数为x人，则植树棵树为(8x7)人，则下面给出的不等式(组)中，能准确求出学生人数与种植树木数量的是(      )A．8x769(x1) B．8x739(x1)C． D．5．(2019·全国八年级单元测试)某企业次定购买，两种型号的污水处理设备共8台，具体情况如下表： 型型价格(万无台)1210月污水处理能力(吨月)200160经预算，企业最多支出89万元购买设备，且要求月处理污水能力不低1380吨，该企业有哪些购买方案呢？这解决这个问题，高购买型污水处理设备台，所列不等式组下确是　　A． B．C． D．6．已知两个语句：①式子的值在1(含1)与3(含3)之间；②式子的值不小于1且不大于3．请回答以下问题：(1)两个语句表达的意思是否一样(不用说明理由)？(2)把两个语句分别用数学式子表示出来．考点4：一元一次不等式组的应用典例：(2020·浙江嘉兴市·八年级期末)某企业新增了一个化工项目，为了节约资源，保护环境，该企业决定购买A、B两种型号的污水处理设备共10台，具体情况如下表：经预算，企业最多支出136万元购买设备，且要求月处理污水能力不低于2150吨． A型B型价格(万元/)1512月污水处理能力(吨/月)250200(1)该企业有哪几种购买方案？(2)哪种方案更省钱？并说明理由．方法或规律点拨此题考查方案类不等式组的实际应用，有理数的混合运算，正确理解题意，根据题意列得不等式组是解题的关键．巩固练习1．(2020·福建省惠安第三中学七年级月考)运行程序如图所示，规定：从“输入一个值”到“结果是否”为一次程序操作，如果程序操作进行了两次就停止，那么的取值范围可能是(   )A． B． C． D．2．(2021·浙江湖州市·八年级期末)为了美化校园，某学校决定利用现有的332盆甲种花卉和310盆乙种花卉，搭配A，B两种园艺造型共50个，摆放在校园道路两侧．已知一个A种园艺造型需甲种花卉7盆，乙种花卉5盆；一个B种园艺造型需甲种花卉6盆，乙种花卉8盆．(1)问搭配A，B两种园艺造型共有几种方案？(2)若一个A种园艺造型的成本是200元，一个B种园艺造型的成本是300元，哪种方案成本最低？请写出此方案．4．(2021·湖南邵阳市·八年级期末)“一方有难，八方相助”是中华民族的优良传统．“新冠肺炎”疫情期间，我市向湖北省某县捐赠A型医疗物资290件和B型医疗物资100件．计划租用甲、乙两种型号的汽车共8辆运送过去．经了解，甲种汽车每辆最多能载A型医疗物资40件和B型医疗物资10件，乙种汽车每辆最多能载A型医疗物资30件和B型医疗物资20件．(1)请你帮助设计所有可能的租车方案；(2)如果甲种汽车每辆的运费是1200元，乙种汽车每辆的运费是1000元，这次运送的费用最少需要多少钱？5．(2021·四川成都市·八年级期末)2020年12月7日，成都市郫都区新增1例本土新冠肺炎确诊病例，让全体市民再次加强了疫情防范意识．某单位准备用3000元购买医用口罩和洗手液发放给全体职工，若医用口罩购买500个，洗手液购买100瓶，则剩余200元；若医用口罩购买800个，洗手液购买80瓶，则还差40元．(1)求医用口罩和洗手液的单价；(2)根据疫情防控实际需要，单位决定购买医用口罩500个，洗手液和酒精消毒喷雾共90瓶，若需购买洗手液的瓶数最多为75瓶且购买酒精消毒喷雾的瓶数不超过洗手液瓶数的，酒精消毒喷雾每瓶的单价是32元，请你设计一种购买方案，要求所花的费用最少，并求出最少费用．6．(2021·湖南娄底市·八年级期末)某校准备组织290名师生进行野外考察活动，行李共有100件．学校计划租用甲、乙两种型号的汽车共8辆，经了解，甲种汽车每辆最多能载40人和10件行李，乙种汽车每辆最多能载30人和20件行李．(1)设租用甲种汽车辆，请你帮助学校设计所有可能的租车方案．(2)如果甲、乙两种汽车每辆车的租车费用分别为2500元和2000元，请你选择最省钱的一种方案．7．(2020·浙江嘉兴市·八年级期末)某商场销售A、B两种型号的计算器，两种计算器的进货价格分别为每台15元，20元．商场销售5台A型号和1台B型号计算器，可获利润38元；销售6台A型号和3台型号计算器，可获利润6元．(1)求商场销售A、B两种型号计算器的销售价格分别是多少元？(2)商场准备用不多于1250元的资金购进A、B两种型号计算器共70台，且全部售出后至少获利460元．问：最少需要购进A型号的计算器多少台？最多可购进A型号的计算器多少台？8．(2020·浙江绍兴市·八年级其他模拟)筹建中的迪荡中学需720套单人课桌椅(如图)，光明厂承担了这项生产任务，该厂生产桌子的必须5人一组．每组每天可生产12张：生产椅子的必须4人一组，每组每天可生产24把．已知学校筹建组要求光明厂6天完成这项生产任务．(1)问光明厂平均每天要生产多少套单人课桌椅？(2)现学校筹建组要求至少提前1天完成这项生产任务．光明厂生产课桌椅的员工增加到84名，试给出一种分配生产桌子、椅子的员工数的方案．9．(2021·广东深圳市·深圳外国语学校八年级期末)某商家欲购进甲､乙两种抗疫用品共180件，其进价和售价如表： 甲乙进价(元/件)1435售价(元/件)2043(1)若商家计划销售完这批抗疫用品后能获利1240元，问甲､乙两种用品应分别购进多少件？(请用二元一次方程组求解)(2)若商家计划投入资金少于5040元，且销售完这批抗疫用品后获利不少于1314元，请问有哪几种购货方案？并直接写出其中获利最大的购货方案．