初中数学华师大版九年级下册2. 二次函数y=ax2+bx+c的图象与性质教学ppt课件

这是一份初中数学华师大版九年级下册2. 二次函数y=ax2+bx+c的图象与性质教学ppt课件，

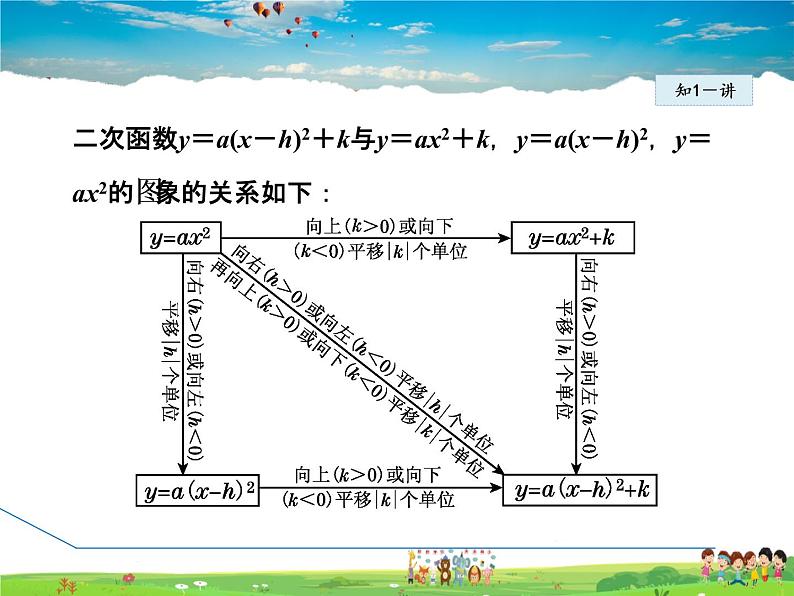
第26章 二次函数26.2 二次函数的图象与性质第4课时 二次函数y=a(x-h)²+k 的图象与性质1课堂讲解二次函数y＝a(x-h)2+k与y＝ax2之间的关系二次函数y＝a(x-h)2+k的图象二次函数y＝a(x-h)2+k的性质2课时流程逐点导讲练课堂小结作业提升 抛物线y=ax2能否通过平移得到y＝a(x－h)2＋k呢？如果能，怎么平移？1知识点知1－导二次函数y=a(x-h)2+k与y=ax2之间的关系知1－讲二次函数y＝a(x－h)2＋k与y＝ax2＋k，y＝a(x－h)2，y＝ax2的图象的关系如下：知1－讲例1 〈泰安〉将抛物线y＝3x2向上平移3个单位，再向左平移 2个单位，那么得到的抛物线对应的函数关系式为(　　) A．y＝3(x＋2)2＋3　　　　　B．y＝3(x－2)2＋3 C．y＝3(x＋2)2－3 D．y＝3(x－2)2－3 由“上加下减”的原则可知，将抛物线y＝3x2向上平移3个单 位所得抛物线对应的函数关系式为y＝3x2＋3；由“左加右 减”的原则可知，将抛物线y＝3x2＋3向左平移2个单位所得 抛物线对应的函数关系式为y＝3(x＋2)2＋3，故选A.A导引：知1－讲 将抛物线在平面直角坐标系中平移，关键是顶点坐标在发生变化，抛物线的形状和大小不变，故紧扣顶点式y＝a(x－h)2＋k中h、k的变化即可．知1－练（来自教材）试说明：分别通过怎样的平移，可以由抛物线 得到抛物线 和抛物 线 如果要得到抛物线 那么应该将抛物线 作怎样的平移？知1－练2 (中考·成都)将抛物线y＝x2向左平移2个单位长度， 再向下平移3个单位长度，得到的抛物线对应的函 数关系式为(　　) A．y＝(x＋2)2－3 B．y＝(x＋2)2＋3 C．y＝(x－2)2＋3 D．y＝(x－2)2－3知1－练(中考·扬州)将抛物线y＝x2＋1先向左平移2个单位长 度，再向下平移3个单位长度，所得抛物线对应的函 数关系式是(　　) A．y＝(x＋2)2＋2 B．y＝(x＋2)2－2 C．y＝(x－2)2＋2 D．y＝(x－2)2－2知1－练把抛物线y＝(x＋1)2向下平移2个单位长度，再向右 平移1个单位长度，所得到的抛物线对应的函数关 系式是(　　) A．y＝(x＋2)2＋2 B．y＝(x＋2)2－2 C．y＝x2＋2 D．y＝x2－22知识点知2－讲二次函数y=a(x-h)2+k的图象知2－讲例2 抛物线y＝3(x－1)2＋2的开口方向、顶点坐标、对 称轴分别是(　　) A．向下、(1，2)、直线x＝1　　 　B．向上、(－1，2)、直线x＝－1 C．向下、(－1，2)、直线x＝－1 D．向上、(1，2)、直线x＝1 抛物线y＝3(x－1)2＋2的开口向上，顶点坐标为(1， 2)，对称轴为直线x＝1，故选D.导引：D知2－讲 本题运用了性质判断法，运用二次函数的性质，结合图象进行判断．试说出函数y = a(x-h)2+k(a、h、k是常数，a≠0)的图象的开口方向、对称轴 和顶点坐标，并填写下表：知2－练（来自教材）2 (中考·新疆)抛物线y＝(x－1)2＋2的顶点坐标是(　　) A．(－1，2) B．(－1，－2) C．(1，－2) D．(1，2)知2－练3 (中考·益阳)若抛物线y＝(x－m)2＋(m＋1)的顶点在第 一象限，则m的取值范围为(　　) A．m＞1 B．m＞0 C．m＞－1 D．－1＜m＜0知2－练4 (中考·兰州)抛物线y＝(x－1)2－3的对称轴是(　　) A．y轴 B．直线x＝－1 C．直线x＝1 D．直线x＝－33知识点二次函数y=a(x-h)2+k的性质知3－讲1. 二次函数y＝a(x－h)2＋k的图象及性质如下表：知3－讲续表：知3－讲要点精析：(1)由于从y＝a(x－h)2＋k(a≠0)中可以直接看出抛物线 的顶点坐标，所以通常把y＝a(x－h)2＋k叫做二次 函数的顶点式；其顶点坐标为(h，k)．(2)二次函数y＝a(x－h)2＋k的图象是一条抛物线，决 定抛物线开口方向的是a的符号，决定开口大小的 是|a|.形状相同，顶点相同时，开口方向相反的两条 抛物线对应的函数表达式的二次项系数互为相反数．知3－讲(3)二次函数y＝a(x－h)2＋k的图象的对称轴与顶点横 坐标的关系：对称轴为直线x＝h，其中h为顶点的 横坐标．2.二次函数y＝a(x－h)2＋k的图象：把二次函数y＝ax2 的图象先向左(h＜0)或向右(h＞0)平移|h|个单位得 到二次函数y＝a(x－h)2的图象，再向上(k＞0)或向 下(k＜0)平移|k|个单位得到二次函数y＝a(x－h)2＋k 的图象．知3－讲二次函数y＝a(x－h)2＋k的图象的平移规律归纳如下表：(其中m>0)知3－讲例3 对于抛物线 y=-（ x+1） 2+3，下列结论： ① 抛物线的开口向下； ② 对称轴为直线 x=1；③ 顶点坐标为（ -1，3）；④ 当 x>1 时， y 随 x 的增大而减小 .其中正确结论有（ ）A. 1 个 B. 2 个 C. 3 个 D. 4 个 C知3－讲①∵ a=-1<0，∴抛物线的开口向下，正确；②对称轴为直线 x=-1，错误；③顶点坐标为（ -1， 3），正确；④当 x>1 时， y 随 x 的增大而减小，正确 .综上所述，正确结论是①③④，共 3 个，故选 C.解： 知3－讲 解答此类题有两种思路，思路一：将三点的横坐标分别代入函数表达式，求出对应的y1，y2，y3的值，再比较大小，但这样计算比较困难，显然不是最佳的方案；思路二：根据二次函数图象的特征来比较，利用增减性以及点在抛物线上的大致位置，关键是这些点与对称轴的位置关系来确定y1，y2，y3的大小，显然这种方法比较简单．知3－练(中考·泰安)对于抛物线y＝－ (x＋1)2＋3，下列结论： ①抛物线的开口向下；②对称轴为直线x＝1；③顶点 坐标为(－1，3)；④x＞1时，y随x的增大而减小，其 中正确的个数为(　　) A．1 B．2 C．3 D．4知3－练已知二次函数y＝a(x－h)2＋k(a＜0)的图象如图所示，当－5≤x≤0时， 下列关于函数值y的说法正确的是(　　) A．有最小值－5，最大值0 B. 有最小值－3，最大值6 C. 有最小值0，最大值6 D. 有最小值2，最大值6知3－练(中考·天津)已知二次函数y＝(x－h)2＋1(h为常数)， 在自变量x的值满足1≤x≤3的情况下，与其对应的 函数值y的最小值为5，则h的值为(　　) A．1或－5 B．－1或5 C．1或－3 D．1或3抛物线y＝a(x－h)2＋k是轴对称图形．函数y＝a(x－h)2＋k的增减性：(1)a>0时，在对称轴x＝h左侧，y随x的增大而减小； 在对称轴x＝h右侧，y随x的增大而增大．(2)a<0时，在对称轴x＝h左侧，y随x的增大而增大； 在对称轴x＝h右侧，y随x的增大而减小．1.必做:完成教材中习题2.补充: 请完成剩余部分习题