人教A版 (2019)必修 第一册3.2 函数的基本性质学案及答案

这是一份人教A版 (2019)必修 第一册3.2 函数的基本性质学案及答案，共12页。学案主要包含了知识点一，知识点二，知识点三，例1-1，例1-2，例3-1，例3-2，例4-1等内容，欢迎下载使用。

1．结合二次函数的图象，判断一元二次方程根的存在性及根的个数，从而了解函数的零点与方程根的联系；
2．掌握零点存在的判定定理．
（预习教材P142~ P144，回答下列问题）
复习1：如何求一元二次方程的实数解呢？
由可得：
当 0，方程有两根，为 ；
当 0，方程有一根，为 ；
当 0，方程无实根．
复习2：一元二次方程的根
与一元二次函数的图象之间有什么关系？
通过上面表格，你有什么发现： ．

【知识点一】函数的零点与方程的解
（1）对于函数，我们把使 的实数叫做函数的 ．
这样，函数的零点就是方程的实数解，也就是函数的图像与轴的交点的横坐标．

（2）函数零点的求法：
代数法：若方程可解，其实数根就是函数的零点．
几何法：若方程难以直接求解，将其改，
进一步改为，在同一坐标系中分别画出两个函数和的图像，两图像交点的横坐标就是函数的零点．
自我检测1-1：函数的图象与轴的交点坐标及其零点分别是 ．
自我检测1-2：函数存在零点吗？若有，你能求出零点吗？
【知识点二】函数零点的存在性定理
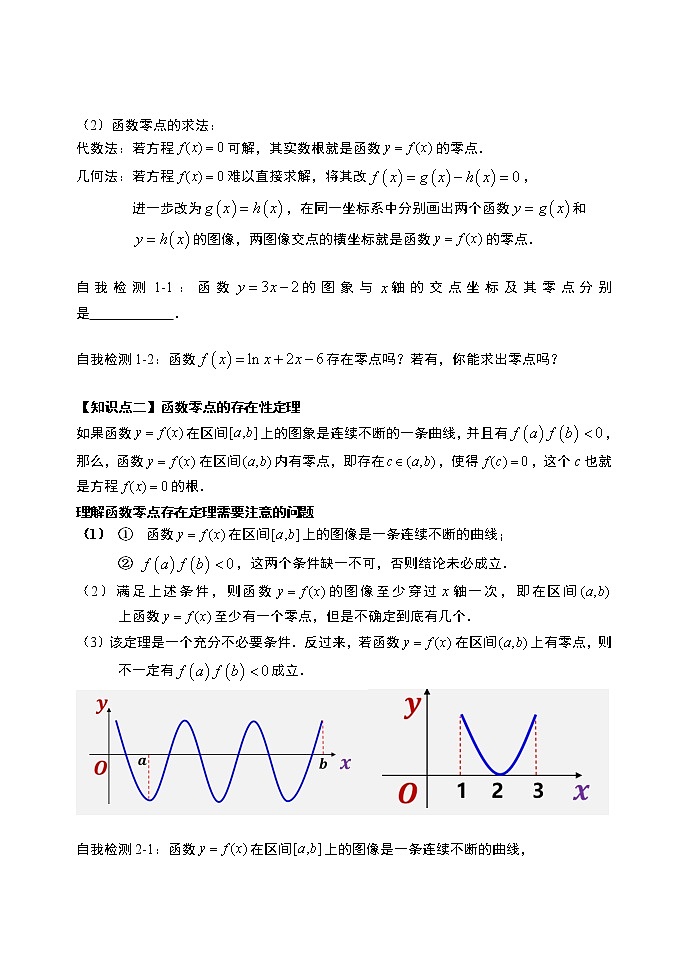
如果函数在区间上的图象是连续不断的一条曲线，并且有，那么，函数在区间内有零点，即存在，使得，这个c也就是方程的根．
理解函数零点存在定理需要注意的问题
（1） ① 函数在区间上的图像是一条连续不断的曲线；
② ，这两个条件缺一不可，否则结论未必成立．
（2）满足上述条件，则函数的图像至少穿过轴一次，即在区间 上函数至少有一个零点，但是不确定到底有几个．
（3）该定理是一个充分不必要条件．反过来，若函数在区间上有零点，则不一定有成立．
自我检测2-1：函数在区间上的图像是一条连续不断的曲线，
在上存在唯一零点
自我检测2-2：函数，你能求出该函数零点的大致范围吗？
【知识点三】常见函数的零点分布情况
题型一 函数零点的概念及求法
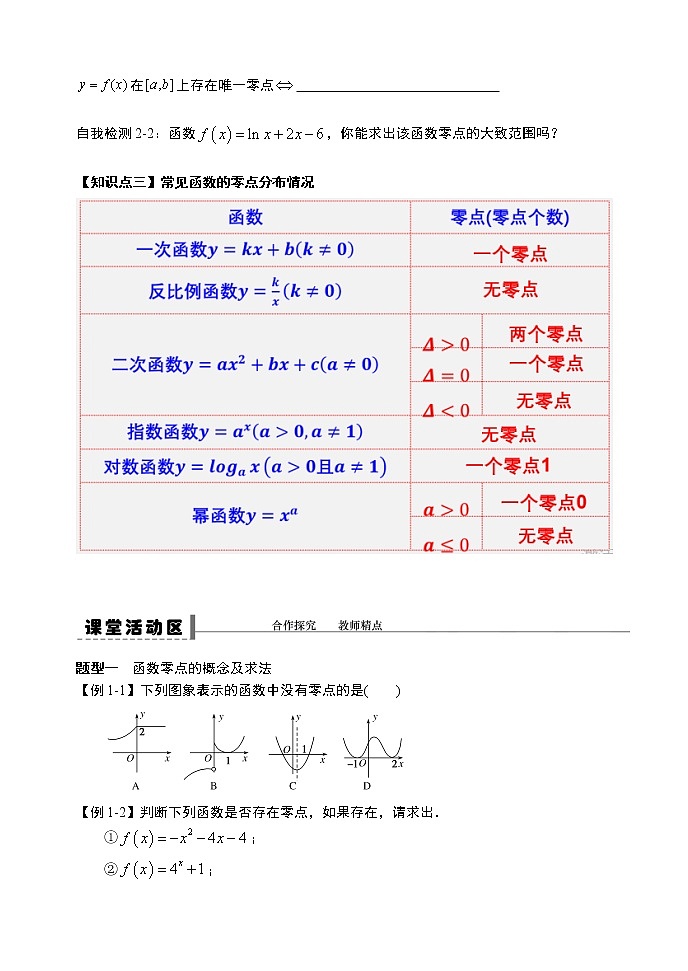
【例1-1】下列图象表示的函数中没有零点的是( )
【例1-2】判断下列函数是否存在零点，如果存在，请求出．
①；
②；
③．
题型二 确定函数零点的个数
【例2】判断下列函数零点的个数
（1） （2）
（3） （4）
题型三 判断函数的零点所在的大致区间
【例3-1】设是函数的零点，则所在的区间为( )
A． B．
C． D．
【例3-2】已知函数，．若存在2个零点，则的取值范围是( )
A． B．
C． D．
题型四 二次型函数的根分布问题
【例4-1】已知函数的零点是和，求函数的零点．
【例4-2】已知二次函数，在下列条件下，求实数的取值范围．
(1)零点均大于1；
(2)一个零点大于1，一个零点小于1；
(3)一个零点在内，另一个零点在内．
1．函数的零点是（ ）
A．B．
C．D．不存在
2．函数在下列区间内一定有零点的是( )
A． B．
C． D．
3．已知函数唯一的零点在区间，，内，那么下列命题不正确的是( )
A．函数在区间或内有零点 B．函数在内无零点
C．函数在内一定有零点 D．函数在内不一定有零点
4．已知，则函数的零点的个数为( )
A．1 B．2
C．3 D．4
5．若二次函数的两个零点分别是和，则的值为________．
§4．5．1 函数的零点与方程的解答案
导学目标：
1．结合二次函数的图象，判断一元二次方程根的存在性及根的个数，从而了解函数的零点与方程根的联系；
2．掌握零点存在的判定定理．
（预习教材P142~ P144，回答下列问题）
复习1：如何求一元二次方程的实数解呢？
由可得：
当 0，方程有两根，为 ；
当 0，方程有一根，为 ；
当 0，方程无实根．
复习2：一元二次方程的根
与一元二次函数的图象之间有什么关系？
通过上面表格，你有什么发现： ．

【知识点一】函数的零点与方程的解
（1）对于函数，我们把使 的实数叫做函数的 ．
这样，函数的零点就是方程的实数解，也就是函数的图像与轴的交点的横坐标．

（2）函数零点的求法：
代数法：若方程可解，其实数根就是函数的零点．
几何法：若方程难以直接求解，将其改，
进一步改为，在同一坐标系中分别画出两个函数和的图像，两图像交点的横坐标就是函数的零点．
自我检测1-1：函数的图象与轴的交点坐标及其零点分别是 ．
【答案】，
自我检测1-2：函数存在零点吗？若有，你能求出零点吗？
【答案】存在
【知识点二】函数零点的存在性定理
如果函数在区间上的图象是连续不断的一条曲线，并且有，那么，函数在区间内有零点，即存在，使得，这个c也就是方程的根．
理解函数零点存在定理需要注意的问题
（1） ① 函数在区间上的图像是一条连续不断的曲线；
② ，这两个条件缺一不可，否则结论未必成立．
（2）满足上述条件，则函数的图像至少穿过轴一次，即在区间 上函数至少有一个零点，但是不确定到底有几个．
（3）该定理是一个充分不必要条件．反过来，若函数在区间上有零点，则不一定有成立．
自我检测2-1：函数在区间上的图像是一条连续不断的曲线，
在上存在唯一零点
自我检测2-2：函数，你能求出该函数零点的大致范围吗？
【答案】

【知识点三】常见函数的零点分布情况
题型一 函数零点的概念及求法
【例1-1】下列图象表示的函数中没有零点的是( )
【例1-2】判断下列函数是否存在零点，如果存在，请求出．
①；
②；
③．
【答案】(1)A (2) ；没有；．
题型二 确定函数零点的个数
【例2】判断下列函数零点的个数
（1） （2）
（3） （4）
【答案】(1)1个 (2) 3个 ；（3）1个；（4）3个．
题型三 判断函数的零点所在的大致区间
【例3-1】设是函数的零点，则所在的区间为( )
A． B．
C． D．
【答案】 C
【例3-2】已知函数，．若存在2个零点，则的取值范围是( )
A． B．
C． D．
【答案】 C
题型四 二次型函数的根分布问题
【例4-1】已知函数的零点是和，求函数的零点．
【答案】
【例4-2】已知二次函数，在下列条件下，求实数的取值范围．
(1)零点均大于1；
(2)一个零点大于1，一个零点小于1；
(3)一个零点在内，另一个零点在内．
【答案】(1)因为方程x2－2ax＋4＝0的两根均大于1，结合二次函数的单调性与零点存在性定理得eq \b\lc\{\rc\ (\a\vs4\al\c1(－2a2－16≥0，,f1＝5－2a＞0，,a＞1，))解得2≤a＜eq \f(5,2)．
即a的取值范围为eq \b\lc\[\rc\)(\a\vs4\al\c1(2，\f(5,2)))．
(2)因为方程x2－2ax＋4＝0的一个根大于1，一个根小于1，结合二次函数的单调性与零点存在性定理得f(1)＝5－2a＜0，解得a＞eq \f(5,2)．
即a的取值范围为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5,2)，＋∞))．
(3)因为方程x2－2ax＋4＝0的一个根在(0,1)内，另一个根在(6,8)内，结合二次函数的单调性与零点存在性定理得eq \b\lc\{\rc\ (\a\vs4\al\c1(f0＝4＞0，,f1＝5－2a＜0，,f6＝40－12a＜0，,f8＝68－16a＞0，))
解得 eq \f(10,3)＜a＜eq \f(17,4).
即a的取值范围为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(10,3)，\f(17,4))).
1．函数的零点是（ ）
A．B．
C．D．不存在
【答案】C
2．函数在下列区间内一定有零点的是( )
A． B．
C． D．
【答案】C
3．已知函数唯一的零点在区间，，内，那么下列命题不正确的是( )
A．函数在区间或内有零点 B．函数在内无零点
C．函数在内一定有零点 D．函数在内不一定有零点
【答案】C
4．已知，则函数的零点的个数为( )
A．1 B．2
C．3 D．4
【答案】B
5．若二次函数的两个零点分别是和，则的值为________．．
【答案】
判别式
一元二次方程的解
一元二次函数图象与轴的交点的横坐标
判别式
一元二次方程的解
一元二次函数图象与轴的交点的横坐标