






2021-2022学年度北师大版九年级中考复习课件 专题三 圆的综合题
展开
这是一份2021-2022学年度北师大版九年级中考复习课件 专题三 圆的综合题,共55页。PPT课件主要包含了专题训练等内容,欢迎下载使用。
专题三 圆的综合题
(9年7考,近5年每年1道解答题)
类型1 与切线性质有关的证明与计算(9年5考:2020、2019、2018、2016、2013)
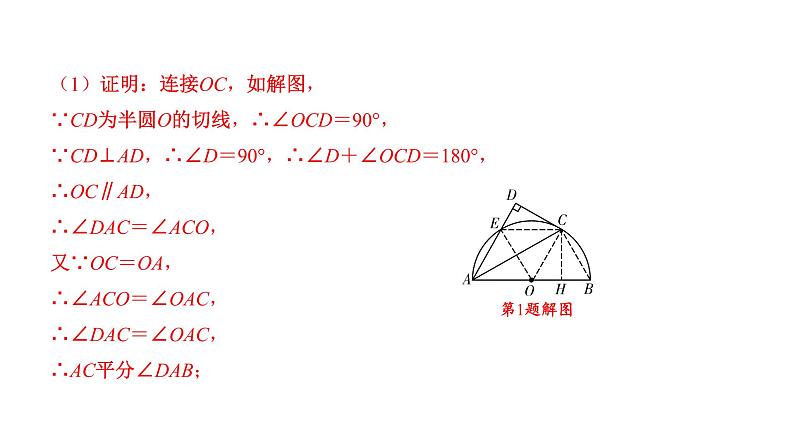
1.(2020十堰)如图,AB为半圆O的直径,C为半圆O上一点,AD与过点C的切 线垂直,垂足为D,AD交半圆O于点E. (1)求证:AC平分∠DAB; (2)若AE=2DE,试判断以O,A,E,C为顶点的四边形的形状,并说明理由.
(1)证明:连接OC,如解图,∵CD为半圆O的切线,∴∠OCD=90°,∵CD⊥AD,∴∠D=90°,∴∠D+∠OCD=180°,∴OC∥AD,∴∠DAC=∠ACO,又∵OC=OA,∴∠ACO=∠OAC,∴∠DAC=∠OAC,∴AC平分∠DAB;
(2)解:四边形EAOC为菱形,理由如下:连接EC、BC、EO,过点C作CH⊥AB于点H,如解图,由圆内接四边形对角互补可知,∠B+∠AEC=180°,又∵∠AEC+∠DEC=180°,∴∠DEC=∠B,又∵∠B+∠CAB=90°,∠DEC+∠DCE=90°,∴∠CAB=∠DCE,又∵∠CAB=∠CAE,∴∠DCE=∠CAE,且∠D=∠D,∴△DCE∽△DAC,∴ = ,设DE=x,则AE=2x,AD=AE+DE=3x,∴CD2=AD·DE=3x2,∴CD= x,
在Rt△ACD中,tan ∠DAC= ,∴∠DAC=30°,∴∠DAO=2∠DAC=60°,∵OA=OE,∴△OAE为等边三角形,由同弧所对的圆周角等于圆心角的一半可知:∠EOC=2∠EAC=60°,OE=OC,∴△EOC为等边三角形,∴EA=AO=OE=EC=CO,即EA=AO=OC=CE,∴四边形EAOC为菱形.
2.(2020陕西)如图,△ABC是⊙O的内接三角形,∠BAC=75°,∠ABC= 45°.连接AO并延长,交⊙O于点D,连接BD.过点C作⊙O的切线,与BA的延 长线相交于点E. (1)求证:AD∥EC; (2)若AB=12,求线段EC的长.
(1)证明:如解图,连接OC,∵CE与⊙O相切于点C,∴∠OCE=90°,∵∠ABC=45°,∴∠AOC=90°,∵∠AOC+∠OCE=180°,∴AD∥EC;
(2)解:如解图,过点A作AF⊥EC交EC于点F,∵∠BAC=75°,∠ABC=45°,∴∠ACB=60°,∴∠D=∠ACB=60°,∵AD是⊙O的直径,∴∠ABD=90°,∴sinD= ,∴AD= ,∴OA=OC= ,∵AF⊥EC,∠OCE=90°,∠AOC=90°,∴四边形OAFC是矩形,又∵OA=OC,∴四边形OAFC是正方形,∴CF=AF=OA=4 ,∵∠BAD=90°-∠D=30°,∴∠EAF=180°-90°-30°=60°,∵tan ∠EAF= ,∴EF= AF=12,∴CE=CF+EF=12+4 .
3.(2020北京)如图,AB为⊙O的直径,C为BA延长线上一点,CD是⊙O的切线 ,D为切点,OF⊥AD于点E,交CD于点F. (1)求证:∠ADC=∠AOF; (2)若sin C= ,BD=8,求EF的长.
(1)证明:如解图,连接OD,∵AB为⊙O的直径,∴∠ADB=90°,∴AD⊥BD,∵OF⊥AD,∴OF∥BD,∴∠AOF=∠B,∵CD是⊙O的切线,D为切点,∴∠CDO=90°,∴∠CDA+∠ADO=∠ADO+∠BDO=90°,∴∠CDA=∠BDO,∵OD=OB,∴∠ODB=∠B,∴∠AOF=∠ADC;
(2)解:由(1)知OF∥BD,AO=OB,∴AE=DE,∴OE= BD= ×8=4,∵sinC= ,∴设OD=x,则OC=3x,OB=x,∴CB=4x,∵OF∥BD,∴△COF∽△CBD,∴ ,∴ ,∴OF=6,∴EF=OF-OE=6-4=2.
4. 如图,AB是⊙O的直径,过点A作⊙O的切线AP,点C是射线AP 上的动点,连接CO交⊙O于点E,过点B作BD∥CO,交⊙O于点 D,连接DE,OD,CD. (1)求证:CA=CD; (2)当四边形EOBD是菱形时,求∠ACO的度数; (3)若BD=m,则当四边形ACDO是正方形时,AC的长度为多少(用含m的式 子表示)?
(1)证明:∵BD∥OC,∴∠AOC=∠OBD,∠DOC=∠ODB,∵OB=OD,∴∠ODB=∠OBD,∴∠AOC=∠DOC,在△AOC和△DOC中, ,∴△AOC≌△DOC(SAS),∴CA=CD;
(2)解:当四边形EOBD是菱形时,OB=BD,∵OB=OD,∴OB=OD=BD,∴△OBD为等边三角形,∴∠OBD=60°,∴∠AOC=∠OBD=60°,∵AP是⊙O的切线,∴∠OAC=90°,∴∠ACO=30°;(3)解:当四边形ACDO是正方形时,AC=OA=OD,∠AOD=90°,∴∠DOB=90°,∵OB=OD,∴OB= ,∴AC=OB= .
5.(2020江西21题9分)已知∠MPN的两边分别与⊙O相切于点A,B,⊙O的半 径为r.(1)如图①,点C在点A,B之间的优弧上,∠MPN=80°,求∠ACB的度数;(2)如图②,点C在圆上运动,当PC最大时,要使四边形APBC为菱形,∠APB 的度数应为多少?请说明理由;(3)若PC交⊙O于点D,求第(2)问 中对应的阴影部分的周长(用含r 的式子表示).
解:(1)如解图①,连接OA,OB,∵PA,PB为⊙O的切线,∴∠PAO=∠PBO=90°,∵∠APB+∠PAO+∠PBO+∠AOB=360°,∴∠APB+∠AOB=180°,∵∠APB=80°,∴∠AOB=100°,∴∠ACB=50°;
(2)当∠APB=60°时,四边形APBC是菱形,理由如下:如解图②,连接OA,OB,由(1)可知,∠AOB+∠APB=180°,∵∠APB=60°,∴∠AOB=120°,∴∠ACB=60°=∠APB,∵点C运动到PC距离最大,∴PC经过圆心,∵PA,PB为⊙O的切线,∴PA=PB,∠APC=∠BPC=30°,又∵PC=PC,∴△APC≌△BPC(SAS),∴∠ACP=∠BCP=30°,AC=BC,∴∠APC=∠ACP=30°,∴AP=AC,∴AP=AC=PB=BC,∴四边形APBC是菱形;(3)阴影部分的周长为 .
6. 已知,AB是⊙O的直径,AB=16,点C在⊙O的半径OA上运动,PC⊥AB,垂 足为C,PC=10,PT为⊙O的切线,切点为T. (1)如图①,当C点运动到O点时,求PT的长; (2)如图②,当C点运动到A点时,连接PO,BT,求证:PO∥BT; (3)如图③,设PT=y,AC=x,求y与x的解析式并求出y的最小值.
(1)解:如解图①,连接OT,则OT⊥PT,∴∠OTP=90°,∵AB是⊙O的直径,AB=16,∴OT= AB=8,在Rt△CTP中,由勾股定理得:PT= ;
(2)证明:如解图②,连接OT,∵PC⊥AB,点C与点A重合,AB是⊙O的直径,∴PA是⊙O的切线,∵PT为⊙O的切线,∴PA=PT,在△OPA和△OPT中, ,∴△OPA≌△OPT(SSS),∴∠AOP=∠TOP= ∠AOT,∵∠AOT=2∠B,∴∠AOP=∠B,∴PO∥BT;
(3)解:如解图③,连接PO,OT,∵AB是⊙O的直径,AB=16,AC=x,∴OC=OA-AC= AB-AC=8-x,OT=8,∵PC⊥AB,∴∠PCO=90°,在Rt△PCO中,由勾股定理得:PO= ,∵PT为⊙O的切线,∴PT⊥OT,在Rt△OTP中,由勾股定理得:y=PT= = = = . ∴当x=8时,y有最小值为6.
类型2 与切线判定有关的证明与计算(9年5考:2019、2018、2017、2014、2013)
1.(2018江西20题8分)如图,在△ABC中,O为AC上一点,以点O为圆心,OC为半径作圆,与BC相切于点C,过点A作AD⊥BO交BO的延长线于点D,且∠AOD=∠BAD. (1)求证:AB为⊙O的切线; (2)若BC=6,tan ∠ABC= ,求AD的长.
(1)证明:如解图,过点O作OE⊥AB于点E,∵AD⊥BO于点D,∴∠ADO=90°,∴∠BAD+∠ABD=90°,∠AOD+∠OAD=90°,∵∠AOD=∠BAD,∴∠ABD=∠OAD,又∵BC为⊙O的切线,∴AC⊥BC,∴∠BCO=∠ADO=90°,∵∠BOC=∠AOD,∴∠OBC=∠OAD=∠ABD,在△BOC和△BOE中,∵ ,∴△BOC≌△BOE(AAS),∴OE=OC,∵OE⊥AB,∴AB是⊙O的切线;
(2)解:∵∠ABC+∠BAC=90°,∠EOA+∠BAC=90°,∴∠EOA=∠ABC,∵tan ∠ABC= ,BC=6,∴AC=BC·tan ∠ABC=8,则AB=10,由(1)知BE=BC=6,∴AE=AB-BE=4,∵tan ∠EOA=tan ∠ABC= ,∴ ,∴OE=3, OB= ,由(1)可知∠ABD=∠OBC,∠ADB=∠ACB=90°,∴△ABD∽△OBC, ∴ ,即 ,∴AD= .
2.(2020宁夏)如图,在△ABC中,∠B=90°,点D为AC上一点,以CD为直径 的⊙O交AB于点E,连接CE,且CE平分∠ACB. (1)求证:AE是⊙O的切线; (2)连接DE,若∠A=30°,求 .
(1)证明:如解图,连接OE,∵CE平分∠ACB,∴∠ACE=∠BCE,又∵OE=OC,∴∠ACE=∠OEC,∴∠BCE=∠OEC,∴OE∥BC,∴∠AEO=∠B,又∵∠B=90°,∴∠AEO=90°,即OE⊥AE,∵OE为⊙O的半径,∴AE是⊙O的切线;
(2)解:如解图,连接DE,∵CD是⊙O的直径,∴∠DEC=90°,∴∠DEC=∠B,又∵∠DCE=∠ECB,∴△DCE∽△ECB,∴ ,∵∠A=30°,∠B=90°,∴∠ACB=60°,∴∠DCE= ∠ACB= ×60°=30°,∴ =cs ∠DCE=cs 30°= ,∴ .
3.(2020于都县模拟)如图①,∠ABC=90°,O为射线BC上一点,OB=4,以 点O为圆心, 长为半径作⊙O交BC于点D,E. (1)当射线BA绕点B按顺时针方向旋转多少度时与⊙O相切?请说明理由; (2)若射线BA绕点B按顺时针方向旋转60°时与⊙O相交于M,N两点,如图 ②,求 的长.
解:(1)当射线BA绕点B按顺时针方向旋转45°或135°时与⊙O相切.理由如下:如解图①,设切点为F,连接OF,则OF⊥BF,在Rt△OBF中,OF= ,OB=4,∴sin ∠OBF= ,∴∠OBF=∠BOF=45°,∴∠ABF=45°,同理:当∠ABF=135°时,AB与⊙O相切,∴当射线BA绕点B按顺时针方向旋转45°或135°时与⊙O相切;
(2)过点O作OH⊥AB于点H,如解图②,∵射线BA绕点B按顺时针方向旋转60°时与⊙O相交于M、N两点,∴∠ABC=30°,∴OH= OB= ×4=2,在Rt△OMH中,OM= ,∴cs ∠MOH= ,∴∠MOH=45°,∴∠MON=90°,∴ 的长为 .
4.(2020福建)如图,AB与⊙O相切于点B,AO交⊙O于点C,AO的延长线交⊙O 于点D,E是 上不与B,D重合的点,sin A= . (1)求∠BED的大小; (2)若⊙O的半径为3,点F在AB的延长线上,且BF= ,求证:DF与⊙O 相切.
(1)解:连接OB,如解图,∵AB与⊙O相切于点B,∴∠ABO=90°,∵sin A= ,∴∠A=30°,∴∠BOD=∠ABO+∠A=120°,∴∠BED= ∠BOD=60°;
(2)证明:连接OF,如解图,∵AB是⊙O的切线,∴∠OBF=90°,∵BF= ,OB=3,∴tan ∠BOF= ,∴∠BOF=60°,∵∠BOD=120°,∴∠BOF=∠DOF=60°,在△BOF和△DOF中, ,∴△BOF≌△DOF(SAS),∴∠OBF=∠ODF=90°,即OD⊥DF,∵OD是⊙O的半径,∴DF与⊙O相切.
5.(2020烟台)如图,在▱ABCD中,∠D=60°,对角线AC⊥BC,⊙O经过点 A,B,与AC交于点M,连接AO并延长与⊙O交于点F,与CB的延长线交于点E ,AB=EB. (1)求证:EC是⊙O的切线; (2)若AD= ,求 的长(结果保留π).
(1)证明:连接OB,如解图,∵四边形ABCD是平行四边形,∴∠ABC=∠D=60°,∵AC⊥BC,∴∠ACB=90°,∴∠BAC=30°,∵BE=AB,∴∠E=∠BAE,∵∠ABC=∠E+∠BAE=60°,∴∠E=∠BAE=30°,∵OA=OB,∴∠ABO=∠OAB=30°,∴∠OBC=30°+60°=90°,∴OB⊥CE,∵点B在⊙O上,∴EC是⊙O的切线;
(2)解:∵四边形ABCD是平行四边形,∴BC=AD= ,过点O作OH⊥AM于点H,连接OM,则四边形OBCH是矩形,∴OH=BC= ,∴OA= =4,∠AOM=2∠AOH=60°,∴ 的长为 .
6. 点B是⊙O外一点,BP是∠ABC的平分线,BA与⊙O的一个交点为D,过点D作 BP的垂线交BP于点E,交BC于点F,交⊙O于点G. (1)如图①,BC与⊙O交于点M和点N,当点G是 的中点时,求证:BA是 ⊙O的切线; (2)如图②,当BC过点O时,画出点 O到BP的距离d,猜想线段FG与 d有怎样的数量关系,并证明.
(1)证明:如解图①,连接OD,OG,∵BP是∠ABC的平分线,∴∠DBE=∠FBE,∵DG⊥BP,∴∠BED=∠BEF=90°,∵BE=BE,∴△DBE≌△FBE(ASA),∴∠BDE=∠BFE,∵∠BFE=∠GFN,∴∠GFN=∠BDE,∵点G是 的中点,∴OG⊥MN,∴∠G+∠GFN=90°,∵OD=OG,∴∠G=∠ODG,∴∠ODG+∠BDF=90°,∴∠BDO=90°,∴OD⊥AB,∵点D在⊙O上,∴BA是⊙O的切线;
(2)解:FG=2d,证明:如解图②,过点O作OH⊥BP于点H,交AB于点M,∴∠BHM=∠BHO=90°,∵BP是∠ABC的平分线,∴∠MBH=∠OBH,∵BH=BH,∴△MBH≌△OBH(ASA),∴OH=HM,∠BMH=∠BOH,∴OM=2OH,连接OD,OG,∵OD=OG,∴∠ODG=∠OGD,∵OM⊥BP,DG⊥BP,∴OM∥DG,∴∠ODG=∠DOM,∠BOM=∠BFD,∴∠DOM=∠G,∴∠BMO=∠DFO,∴∠DMO=∠OFG,∵OD=OG,∴△ODM≌△GOF(AAS),∴OM=FG,∴FG=2OH,即FG=2d.
7.(2020九江市模拟)如图,已知AB是⊙O的直径,BE是⊙O的弦,BC是∠ABE 的平分线且交⊙O于点C,连接AC,CE,过点C作CD⊥BE,交BE的延长线于 点D.(1)∠DCE ∠CBE;(填“>”“<”或“=”)(2)求证:DC是⊙O的切线;(3)若⊙O的直径为10,sin∠BAC= ,求BE的长.
(1)解:=;【解法提示】∵AB为⊙O的直径,∴∠ACB=90°,∵CD⊥BE,∴∠D=90°,∴∠ACB=∠D,∵BC是∠ABE的平分线,∴∠ABC=∠CBD,∴△ABC∽△CBD,∴∠BAC=∠BCD,∵四边形ABEC是圆内接四边形,∴∠CED=∠BAC,∴∠BCD=∠CED,∵∠DBC+∠BCD=90°,∠ECD+∠CED=90°,∴∠DCE=∠CBE;
(2)证明:如解图,连接OC,∵OB=OC,∴∠OBC=∠OCB,∵∠ABC=∠CBD,∴∠OCB=∠CBD,∴OC∥BD,∵CD⊥BD,∴OC⊥CD,∵点C在⊙O上,∴CD是⊙O的切线;
(3)解:∵⊙O的直径为10,sin ∠BAC= ,∴sin ∠BAC= ,∴BC=8,∴AC= ,∵△ABC∽△CBD,∴ ,即 ,∴CD=4.8,BD=6.4,∵∠CDE=∠ACB=90°,∠CED=∠BAC,∴△CED∽△BAC,∴ ,即 ,∴DE=3.6,∴BE=BD-DE=6.4-3.6=2.8.
8.(2020江西样卷四)如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=2 ,以点A为圆心,AC长为半径的圆交CA的延长线于点D,作DE∥AB交⊙A于 点E,直线EB交射线AC于点F. (1)求证:直线 EF是⊙A的切线; (2)点P是半径AC上的动点,以点P为圆 心,4为半径的⊙P交直线EF于点M, N.当△MPN是直角三角形时,如图② 所示,求AP的长.
(1)证明:如解图①,连接AE.∵AE=AD,∴∠AED=∠ADE.又∵DE∥AB,∴∠AED=∠EAB,∠CAB=∠ADE,∴∠CAB=∠EAB.∵AC=AE,AB=AB,∴△CAB≌△EAB,∴∠AEB=∠ACB=90°,∴AE⊥EF,∵AE是⊙A的半径,∴直线EF是⊙A的切线;
(2)解:如解图②,连接AE,过点P作PH⊥EF于点H.∵等腰Rt△PMN,PM=PN=4,∴PH= . ∵∠AEB=∠ACB=90°,∴△FBC∽△FAE,∴ ,∴EF=2CF. 设CF=x,∴EF=2x,由(1)知BE=BC=2,∴FB=2x-2,∴在Rt△BCF中,(2x-2)2=22+x2,∴x= 或x=0(舍去).∵PH∥AE,∴△FPH∽△FAE,∴ .设AP=y,∴ ,∴y= ,即AP的长为 .
9.(2020江西样卷一)如图,AB是⊙O的直径,AB=BD,DO交⊙O于点F,点E 是线段OF上一动点,连接BE并延长交⊙O于点C,连接AC,tan ∠ABC的值会 随着点E的运动而发生变化. (1)如图①,当tan ∠ABC= ,AC∥OE时, 求证:直线BD是⊙O的切线; (2)如图②,当tan ∠ABC=1,直线BD与⊙O 相切,AB=4时, ①求CD的长;②求 的值.
(1)证明:∵AB是直径.∴∠C=90°.∵tan ∠ABC= ,∴AC= BC.∵AC∥OD,∴OD⊥BC,∴BE= BC,∴AC=BE.∵AB=DB,∴Rt△ACB≌Rt△BED,∴∠A=∠DBE.∵∠A+∠ABC=90°,∴∠DBE+∠ABC=90°,即∠DBO=90°,∴BD⊥AB,∵AB是⊙O的直径,∴BD是⊙O的切线;
(2)解:①∵直线BD是⊙O的切线,∴∠ABD=90°.∵tan ∠ABC=1,AB是直径,AB=4,∴∠ABC=45°,AC=BC= ,∴∠DBC=45°,∴∠ABC=∠DBC.∵AB=BD,BC=BC,∴△ABC≌△DBC,∴AC=DC= ;
10.(2020江西样卷五)如图,在⊙O中,OA=OB=6,∠AOB=120°,点P是AB上一动点,PC⊥OP,且PC=OP.(1)如图①,若点P与点A重合,则PC与⊙O的位置关系是 ;(2)如图②,过点C作CD⊥AB于点D,则PD的长是否是一个定值?若是,则PD= ;若不是,请简述理由;(3)如图③,若点C落在⊙O上,求PA的长.
图① 图② 图③ 备用图
解:(1)相切;(2)是,3;(3)过点O作OE⊥AB于点E,连接OC.在△OBA中,OA=OB=6,∠AOB=120°,∴∠A=30°,OE=3,AE= .∵PO=PC,PC⊥PO,∴△OPC是等腰直角三角形.∵点C在⊙O上,OC=6,∴OP= ,∴PE= .①当点C落在劣弧AB上时,如解图①,AP=AE-PE= -3;②当点C落在优弧AB上时,如解图②,AP=AE+PE= +3;∴当点C落在⊙O上时, AP= 3.
相关课件
这是一份北师大版九年级下册第三章 圆综合与测试教学课件ppt,共9页。
这是一份九年级中考数学专题复习课件 圆的综合题,共60页。PPT课件主要包含了第1题图,第1题解图,第2题图,第2题解图,第3题图,第3题解图,第4题图,第3题解图①,第3题解图②,第4题图①等内容,欢迎下载使用。
这是一份初中数学北师大版九年级下册5 确定圆的条件备课ppt课件,共11页。PPT课件主要包含了确定圆的条件,三点定圆,三角形与圆的位置关系,结束寄语等内容,欢迎下载使用。



![2021-2022学年度北师大版九年级中考复习课件 专题七 二次函数综合题 [Repaired]](http://jx-previews-01.oss-cn-hangzhou.aliyuncs.com/2/3/12286897/0/0.jpg?x-oss-process=image/resize,w_202)




