2021-2022学年度北师大版九年级中考复习课件 专题四 实物情景应用题

这是一份2021-2022学年度北师大版九年级中考复习课件 专题四 实物情景应用题，共60页。PPT课件主要包含了专题训练，第1题图，第2题图，不稳定性，三角形具有稳定性等内容，欢迎下载使用。
专题四　实物情景应用题 （近9年每年1道）
类型1　三角形模型（9年7考：2015－2020、2012）
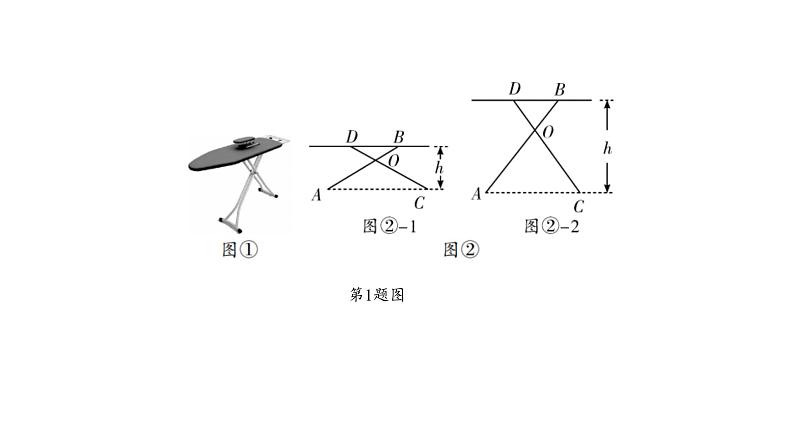
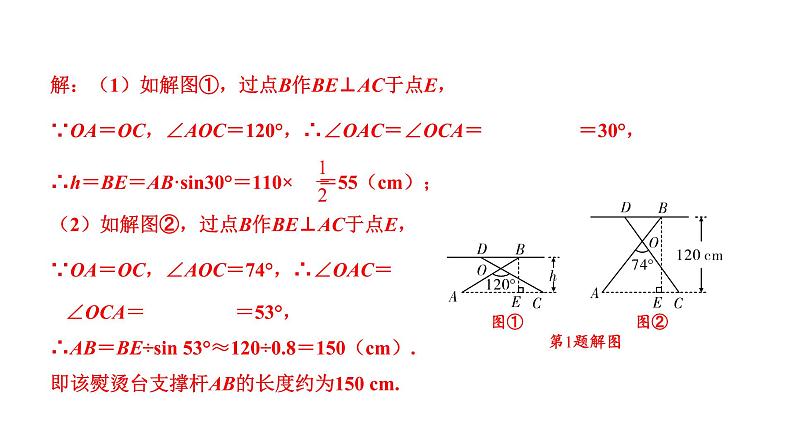
1.（2020湖州）有一种升降熨烫台如图①所示，其原理是通过改变两根支撑杆夹 角的度数来调整熨烫台的高度．图②是这种升降熨烫台的平面示意图，AB和 CD是两根相同长度的活动支撑杆，点O是它们的连接点，OA＝OC，h（cm） 表示熨烫台的高度． （1）如图②－1，若AB＝CD＝110 cm，∠AOC＝120°，求h的值； （2）爱动脑筋的小明发现，当家里这种升降熨烫台的高度为120 cm时，两根 支撑杆的夹角∠AOC是74°（如图②－2）.求该熨烫台支撑杆AB的长度 （结果精确到1 cm）． （参考数据：sin37°≈0.6，cs37°≈0.8，sin53°≈0.8，cs53°≈0.6）
解：（1）如解图①，过点B作BE⊥AC于点E，∵OA＝OC，∠AOC＝120°，∴∠OAC＝∠OCA＝ ＝30°，∴h＝BE＝AB·sin30°＝110× ＝55（cm）；（2）如解图②，过点B作BE⊥AC于点E，∵OA＝OC，∠AOC＝74°，∴∠OAC＝ ∠OCA＝ ＝53°，∴AB＝BE÷sin 53°≈120÷0.8＝150（cm）.即该熨烫台支撑杆AB的长度约为150 cm.
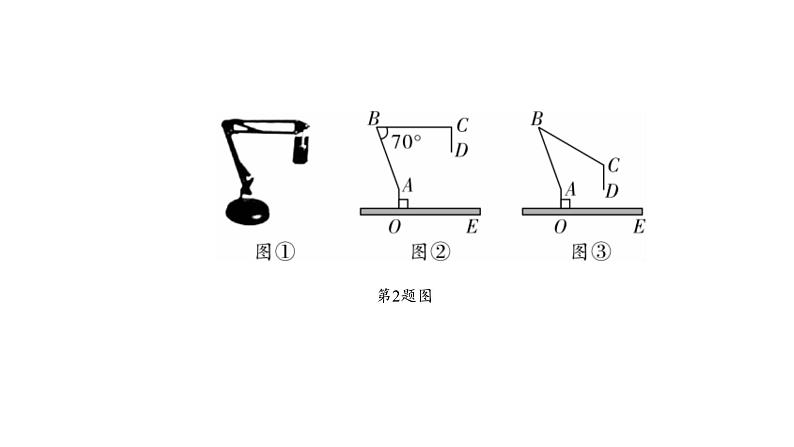
2.（2019江西20题8分）图①是一台实物投影仪，图②是它的示意图，折线B －A－O表示固定支架，AO垂直水平桌面OE于点O，点B为旋转点，BC可转动 ，BC绕点B顺时针旋转时，投影探头CD始终垂直于水平桌面OE，经测量： AO＝6.8 cm，CD＝8 cm，AB＝30 cm，BC＝35 cm. （结果精确到0.1）. （1）如图②，∠ABC＝70°，BC∥OE. ①填空：∠BAO＝ °； ②求投影探头的端点D到桌面OE的距离； （2）如图③，将（1）中的BC向下旋转，当投影探头的端点D到桌面OE的距离 为6 cm时，求∠ABC的大小. （参考数据：sin70°≈0.94，cs20°≈0.94， sin36.8°≈0.60，cs53.2°≈0.60）
解：（1）①160；②如解图①，过点A作AF⊥BC于点F，则AF＝AB·sin ∠ABF＝30sin70°≈28.2（cm），∴投影探头的端点D到桌面OE的距离为：AF＋OA－CD≈28.2＋6.8－8＝27.0（cm）；
（2）如解图②，作DH⊥OE于点H，过点B作BM⊥CD，与DC的延长线相交于点M，过A作AF⊥BM于点F，则∠MBA＝70°，AF≈28.2 cm，DH＝6 cm，BC＝35 cm，CD＝8 cm，AO＝6.8 cm，∴CM＝AF＋AO－DH－CD≈28.2＋6.8－6－8＝21（cm），∴sin ∠MBC＝ ＝0.6，∴∠MBC＝36.8°，∴∠ABC＝∠ABM－∠MBC＝33.2°.
3.（2020新余市模拟）图①是一种电脑桌的实物图，此电脑桌的桌面可调节，图②和图③是其可调节桌面的侧面示意图，在点C处固定安装了一根长度一定的支撑臂CB.点B可在AD上滑动，AC＝25 cm.（1）在图②中，当BC⊥AC时，测得∠A＝45°，求支撑臂CB的长；（2）在图③中，当BC与AC不垂直时，测得∠BAC＝22°，求此时AB的长；（3）从图②到图③过程中，求点C在此运动过程中的路径长．（参考数据：sin22°≈0.37，cs22°≈0.93，tan22°≈0.40，π≈3.14，结果保留到0.1 cm）
解：（1）∵AC⊥BC，∠A＝45°，∴∠ACB＝90°，∠CBA＝∠A＝45°，∴BC＝AC＝25（cm）；（2）如解图，过点C作CH⊥AB于点H.∵AC＝CB，CH⊥AB，∴AH＝HB＝AC·cs22°≈23.25（cm），∴AB＝2AH≈46.5（cm）；（3）∵AC旋转的角度为45°－22°＝23°，∴点C在此运动过程中的路径长为 ≈10.0（cm）.
4.（2020江西样卷七）某电水壶采用的是蒸气智能感应控温，具有水沸腾后自动 断电、防干烧断电的功能．如图①，将壶盖打开时，壶盖与闭合时盖面之间 的夹角可抽象为∠AOB，壶身侧面与底座（壶盖及底座厚度忽略不计）之间 的夹角可抽象为∠ODC（如图②）．若壶嘴及手柄部分不考虑，量得壶盖直 径和底座直径分别为8 cm，12 cm，∠ODC＝80°. （1）求底座周长比壶盖周长长多少；（结果保留π） （2）将壶盖打开时，若量得∠AOB＝74°，求壶盖最高点A距离底座所在平面 的高度．（参考数据：sin74°≈ ，sin80°≈ ，tan74°≈ ， tan80°≈ ，结果精确到0.1 cm）
解：（1）由题知，壶盖及底座的周长分别为8π cm，12π cm.∴底座周长比壶盖周长长12π －8π＝4π（cm）；（2）如解图，过点A作AE⊥OB于点E，过点O作OF⊥CD于点F，则△AOE和△ODF均为直角三角形．∵壶盖和底座的直径分别为8 cm，12 cm，∴OA＝8 cm，DF＝2 cm.∵∠AOB＝74°，∠ODC＝80°，∴AE＝OA·sin 74°≈8× ＝7.68（cm），OF＝DF·tan 80°≈2× ＝11.34（cm）.∴壶盖最高点A距离底座所在平面的高度为AE＋OF≈7.68＋11.34≈19.0（cm）.
5.（2020江西样卷六）某班为了营造书香教室，培养学生阅读的习惯，在教室一 角放置了一种创意书架（如图①），书架由七块长度一样的长木板拼接而成，其中三块横向长木板与地面平行，另外四块拼成双“A”形状，若忽略其厚度， 其基本结构可简化为图②.已知点A，C，E在地面上，AB∥CD，BC∥DE，AB ＝BC＝CD＝DE＝AE＝200 cm.（1）求书架的高度（即点B到地面的距离）；（2）现有一批厚度均为2 cm，高度均为35 cm的图书，若要将此种图书按图② 所示方式自然竖放在阴影部分这一格子中，已知阴影部分格子的层高为 62.5 cm，阴影部分格子的底边长为84 cm，则阴影部分格子中最多可摆放 多少本这样的图书？（参考数据： ≈3.87）
解：（1）如解图，过点B作BF⊥AE于点F.∵AB∥CD，BC∥DE，AB＝BC＝CD＝DE，∴∠BAC＝∠BCA＝∠DEC＝∠DCE，∴△BAC≌△DCE，∴AC＝CE＝ AE＝100 cm.∵AB＝BC，BF⊥AE，∴AF＝ AC＝50 cm.∴BF＝ ，即书架的高度约为193.5 cm；（2）如解图，∵MH∥AE，∴∠GMH＝∠BAF.∵∠GHM＝∠BFA＝90°，∴△GMH∽△BAF，∴ ，即 ，得MH≈9（cm）.∴最多可以放置图书（84－9×2）÷2＝33（本）.
6.（2020衢州改编）图①是由七根连杆链接而成的机械装置，图②是其示意 图．已知O，P两点固定，连杆PA＝PC＝140 cm，AB＝BC＝CQ＝QA＝60 cm ，OQ＝50 cm，O，P两点间距与OQ长度相等．当OQ绕点O转动时，点A，B ，C的位置随之改变，点B恰好在线段MN上来回运动．当点B运动至点M或N时 ，点A，C重合，点P，Q，A，B在同一直线上（如图③）. （1）求点P到MN的距离； （2）当点P，O，A在同一直线上时，点Q到MN的距离为多少？
解：（1）如解图①，延长PO交MN于点T，过点O作OH⊥PQ于点H.由题意得OP＝OQ＝50 cm，PQ＝PA－AQ＝140－60＝80（cm），PM＝PA＋BC＝140＋60＝200（cm），PT⊥MN.∵OH⊥PQ，∴PH＝HQ＝ PQ＝40（cm）.∵csP＝ ，∴ ，∴PT＝160（cm），∴点P到MN的距离为160 cm；
（2）如解图②，当O，P，A共线时，过点Q作QH⊥PT于点H.设HA＝x cm.由题意得AT＝PT－PA＝160－140＝20（cm），OA＝PA－OP＝140－50＝90（cm），OQ＝50 cm，AQ＝60 cm，∵QH⊥OA，∴QH2＝AQ2－AH2＝OQ2－OH2，∴602－x2＝502－（90－x）2，解得x＝ ，∴HT＝AH＋AT＝ （cm），∴当点P，O，A在同一直线上时，点Q到MN的距离为 cm.
7.（2020江西样卷四）图①是家用“垂直式蒸汽除皱熨烫机”，由底座（主机）、 支撑杆、活动衣架和熨烫头组成．图②是其平面抽象示意图，矩形ABMN为底 座，CF为支撑杆，CF⊥AB.现测得底座高AN＝34 cm，固定杆CD＝38 cm，DE 是可伸缩杆，衣架宽GH＝46 cm，且GH⊥DF，∠G＝∠H＝15°.衣架E处的 左右是活扣，解开E处左活扣后，FG可绕点F逆时针旋转至支撑杆，EG可绕点 G顺时针旋转的最大角度是105°（如图③）． （1）求衣架的高EF； （2）解开E处活扣后，FG自然旋转至支撑杆，EG旋转至最大角度，伸缩杆ED 完全缩起，求此时点E离地面的高度. （结果精确到0.1 cm.参考数据： sin15° ≈0.26, cs15°≈0.97，tan15°≈0.27）
解：（1）∵∠G＝∠H＝15°，∴FG＝FH.∵GH⊥DF，∴GE＝EH＝ GH＝23（cm）.在Rt△FGE中，∵tan15°＝ ，∴EF≈0.27×23≈6.2（cm）.∴衣架的高EF约为6.2 cm；
（2）如解图，在Rt△FGE中，cs15°＝ ，∴GF≈23.7（cm），∴G′F＝GF≈23.7（cm），∴G′D＝G′F－EF≈23.7－6.2＝17.5（cm）.由题意，知∠FG′E′＝105°＋15°＝120°，作E′P⊥CF于点P，则∠E′＝30°，∴G′P＝ G′E′＝ GE＝11.5（cm），∴CP＝CD－G′D－G′P≈38－17.5－11.5＝9.0（cm），∴CP＋AN＝9.0＋34＝43.0（cm），∴此时点E离地面的高度约为43.0 cm.
8.（2020衡阳）小华同学将笔记本电脑水平放置在桌子上，当显示屏的边缘线 OB与底板的边缘线OA所在水平线的夹角为120°时，感觉最舒适（如图①）． 侧面示意图为图②；使用时为了散热，他在底板下面垫入散热架，如图③，点 B，O，C在同一直线上，OA＝OB＝24 cm，BC⊥AC，∠OAC＝30°. （1）求OC的长； （2）如图④，垫入散热架后，要使显示屏的边缘线OB′与水平线的夹角仍保持 120°，求点B′到AC的距离．（结果保留根号）
解：（1）在Rt△AOC中，∵OA＝24 cm，∠OAC＝30°.∴OC＝ OA＝ ×24＝12（cm）；（2）如解图，过点B′作B′D⊥AC，垂足为D，过点O作OE⊥B′D，垂足为E，由题意得，OA＝OB′＝24（cm），当显示屏的边缘线OB′与水平线的夹角仍保持120°时，可得∠AOB′＝150°，∴∠B′OE＝60°.∵∠ACO＝∠B′EO＝90°，∴在Rt△B′OE中，B′E＝OB′×sin60°＝ （cm），又∵OC＝DE＝ （cm），∴B′D＝B′E＋DE＝ ＋12（cm），即点B′到AC的距离为（12＋ ）cm.
9.（2020南昌市二模）如今，不少人在购买家具时追求简约大气的风格，图①所 示的是一款非常畅销的简约落地收纳镜，其支架的形状固定不变，镜面可随 意调节，图②所示的是其侧面示意图，其中OD为镜面，EF为放置物品的收纳 架，AB，AC为等长的支架，BC为水平地面，已知OA＝44 cm，OD＝120 cm ，BD＝40 cm，∠ABC＝75°.（结果精确到1 cm.参考数据：sin75°≈0.97， cs75°≈ 0.26，tan75°≈3.73， ≈1.41， ≈1.73） （1）求支架顶点A到地面BC的距离； （2）如图③，将镜面顺时针旋转15°，求此时收纳镜顶部端点O到地面BC的 距离．
解：（1）如解图①，过点A作AI⊥BC于点I.∵OA＝44 cm，OD＝120 cm，∴AD＝OD－OA＝76 cm，∵BD＝40 cm，∴AB＝AD＋BD＝76＋40＝116（cm）.∵∠ABC＝75°，∴在Rt△ABI中，AI＝AB·sin75°≈116×0.97≈113（cm）；答：支架顶点A到地面BC的距离约为113 cm.
（2）如解图②，过点O作OG⊥BC于点G.过点A作AH⊥OG于点H，∵∠BAC＝30°，∠DAE＝15°，∴∠OAC＝135°，∵∠HAI＝90°，∠CAI＝15°，∴∠HAC＝75°，∴∠OAH＝60°，∴OH＝OA·sin60°＝44× ＝ （cm）.∵HG＝AI≈113 cm，∴OG＝OH＋HG≈ ＋113≈151（cm）.答：端点O到地面BC的距离为151 cm.
10.（2020江西样卷八）图①是某校外墙安装的一款红外线监控摄像头，图②是其 简单抽象示意图．点O为摄像头的光源，由光源O射出的红外线形成光线OB ，OC，摄像头上下平移时，红外线的张角∠BOC不变．已知∠BOC＝60°， ∠AOB＝15°，OA垂直于地面且OA＝3 m. （1）求该摄像头能监控到的地面上的最大宽度BC； （2）若距离OA 18 m处有一辆汽车，要使摄像头能监控到该辆汽车，应将摄 像头沿墙面向上至少平移多少米？（不考虑其他因素，结果精确到0.01 m）（参考数据：sin15°≈0.26，sin75°≈0.97，tan15°≈0.27，tan75°≈3.73）
解：（1）在Rt△AOB中，OA＝3，∠AOB＝15°，∵tan ∠AOB＝ ，∴tan15°＝ ，即AB＝3tan15°≈3×0.27＝0.81（m）.在Rt△AOC中，OA＝3，∵∠AOC＝∠BOC＋∠AOB＝75°，∴∠ACO＝15°.∵tan ∠ACO＝ ，∴tan15°＝ ，即AC＝ ≈11.11（m）.∴BC＝AC－AB≈11.11－0.81＝10.30（m）；
（2）如解图，设将摄像头向上平移x m到点P处，刚好能监控到该辆汽车，设该辆汽车位于点Q.由题意可知，OB∥PD，OC∥PQ，∠DPQ＝∠BOC＝60°，∠APD＝∠AOB＝15°，在Rt△APQ中，AP＝3＋x，∠APQ＝∠APD＋∠DPQ＝15°＋60°＝75°.∵tan ∠APQ＝ ，∴tan 75°＝ ，即3.73×（3＋x）≈18，解得x≈1.83.∴应将摄像头沿墙面向上至少平移1.83 m．
11. 图①是一款“雷达式”懒人椅．当懒人椅完全展开时，其侧面示意图如图②所 示，金属杆AB，CD在点O处连接，且分别与金属杆EF在点B，D处连接．金 属杆CD的OD部分可以伸缩（即OD的长度可变）．已知OA＝50 cm，OB＝ 20 cm，OC＝30 cm.DE＝BF＝5 cm.当把懒人椅完全叠合时，金属杆AB，CD ，EF重合在一条直线上（如图③所示），此时点E和点A重合. （1）如图②，已知∠BOD＝6∠ODB，∠OBF＝140°. ①求∠AOC的度数； ②求点A，C之间的距离； （2）如图③，当懒人椅完全叠合时，求CF与CD的长.
解：（1）①∵∠OBF＝∠BOD＋∠ODB，∠BOD＝6∠ODB，∴6∠ODB＋∠ODB＝∠OBF，∴7∠ODB＝140°，∴∠ODB＝20°，∴∠BOD＝6×20°＝120°.∵∠AOC＝∠BOD，∴∠AOC＝120°；②连接AC，过点A作AG⊥CD于点G，如解图，∵∠AOC＝120°，∴∠AOG＝180°－120°＝60°.∵AG⊥CD，∴∠OGA＝90°，∴∠OAG＝90°－60°＝30°，∴OG＝ OA＝ ×50＝25（cm），
由勾股定理得：AG＝ （cm）.∵CG＝OC＋OG＝30＋25＝55（cm），∴AC＝ ＝70（cm），∴点A，C之间的距离为70 cm；（2）CF＝OC－OB－BF＝30－20－5＝5（cm），CD＝OC＋OA－DE＝30＋50－5＝75（cm），即CF的长为5 cm，CD的长为75 cm.
类型2　四边形模型（2014）
1.（2020绍兴）如图①为搭建在地面上的遮阳棚，图②、图③是遮阳棚支架的示 意图．遮阳棚支架由相同的菱形和相同的等腰三角形构成，滑块E，H可分别 沿等长的立柱AB，DC上下移动，AF＝EF＝FG＝1 m.（1）若移动滑块使AE＝EF，求∠AFE的度数和棚宽BC的长．（2）当∠AFE由60°变为74°时，问棚宽BC是增加还是减少？增加或减少了多 少？（结果精确到0.1 m，参考数据： ≈1.73，sin37°≈0.60，cs37°≈0.80，tan37°≈0.75）
解：（1）∵AE＝EF＝AF＝1，∴△AEF是等边三角形，∴∠AFE＝60°，如解图，连接MF并延长交AE于点K，则FM＝2FK，∵△AEF是边长为1的等边三角形，∴AK＝ m，∴FK＝ m，∴FM＝2FK＝ m，∴BC＝4FM＝ ≈6.92≈6.9（m）；（2）∵∠AFE＝74°，∴∠AFK＝37°，∴KF＝AF·cs37°≈0.80 m，∴FM＝2FK≈1.60 m，∴BC＝4FM≈6.40 m＜6.92 m，6.92－6.40＝0.52≈0.5(m).答：当∠AFE由60°变为74°时，棚宽BC是减少了， 减少了0.5 m．
2. 如图①是某工厂生产的多功能儿童滑板车示意图，已知前后车轮半径相同， 车杆AB的长为100 cm，点D是AB的中 点，前支撑板DE＝50 cm，支撑点E在 水平线BC上，∠B＝53°.（参考数 据：sin53°≈0.80，cs53°≈0.60， tan53°≈1.33）（1）求支撑点E与前轮轴心B之间的距离BE的长；（2）根据需要，滑板车可变形为如图②所示的自行车，前支撑板DE变形为座板 后与水平面BC平行，后支撑板EC＝60 cm，求变形后两轴心之间的距离BC 的长．
解：（1）如解图①，过点D作DF⊥BE于点F，由题意知BD＝DE＝50 cm，∠B＝53°，∴BF＝BD cs ∠B≈50×0.6＝30（cm），∴BE＝2BF＝60 cm；
（2）如解图②，过点D作DM⊥BC于点M，过点E作EN⊥BC于点N，由题意知四边形DENM是矩形，∴MN＝DE＝50 cm，在Rt△DBM中，BM＝BD csB≈50×0.6＝30（cm），EN＝DM＝BD sin B≈50 ×0.8＝40（cm)，在Rt△CEN中，∵CE＝60 cm，∴CN＝ cm，则BC＝30＋50＋ ＝（80＋ ）（cm）.
3.疫情期间部分学生选择在家用电视观看网络课程，为了保护眼睛，电视机的安 装高度有一定的要求．如图所示，小嘉家的壁挂电视机的安装高度AB为1米，电 视的中心位置D（AC的中点）比平视视线EF低8 cm（这样观看眼睛最不容易 疲劳），电视机宽度AC为60 cm，眼到 凳子平面的高度EH为75 cm. （1）求小嘉应选用凳子的高度； （2）若看电视的视角∠CEF为3°时， 观看感最好，求此时凳子中心H到 墙AB的距离（电视机的厚度忽略不计）.（参考数据：sin3°≈0.052 3， cs3°≈0.999 7，tan3°≈0.055 0）
解：（1）如解图，作HP⊥BC于点P，则四边形PBGH、FPHE为矩形，∴BF＝GE，PF＝HE＝75 cm.∵AD＝ AC＝30 cm，∴BF＝BA＋AD＋DF＝100＋30＋8＝138（cm），∴HG＝PB＝BF－PF＝138－75＝63（cm）.即小嘉应选用凳子的高度为63 cm；（2）在Rt△CEF中，tan ∠CEF＝ ≈0.055 0.∵CF＝CD－DF＝22 cm，∴BG＝EF≈22÷0.055 0＝400（cm），∴此时凳子中心H到墙AB的距离约为400 cm.
4.（2020江西省模拟）某班为了培养学生的阅读习惯，在教室一角放置了一种创 意书架，如图①所示．书架可看作由 两个相同的平行四边形木制格子叠合 而成，忽略其厚度，其平面示意图可 简化为图②，测得▱ABCD与▱EFGH 中，∠B＝∠F＝80°，AD＝45 cm， AB＝30 cm，且BI＝14 cm，FI＝8 cm，FG∥BC. （1）依题意可知，DJ＝ cm，JH＝ cm，∠CJH＝ °； （2）求书架的高度和宽度．（参考数据：sin80°≈0.98，cs80°≈0.17， tan80°≈5.67.结果保留一位小数）
解：（1）8；14；100；（2）过点A作AM⊥BC于点M，过点F作FN⊥BC于点N，∵∠B＝∠EIC＝∠FIN＝80°，AB＝30，FI＝8，∴AM＝AB·sin80°≈30×0.98＝29.4，FN＝IF·sin80°≈8×0.98＝7.84，∴书架的高度为AM＋FN＝29.4＋7.84≈37.2 cm，过点A作AP⊥CD于点P，过点H作HQ⊥CD于点Q，∵∠D＝∠DJH＝80°，AD＝45，HJ＝14，∴AP＝AD·sin80°≈45×0.98＝44.1，HQ＝HJ·sin80°≈14×0.98＝13.72，∴书架的宽度为AP＋HQ＝44.1＋13.72≈57.8 cm.
5.（2019上海）图①是某小型汽车的侧面示意图，其中矩形ABCD表示该车的后备 箱，在打开后备箱的过程中，箱盖ADE可以绕点A逆时针方向旋转，当旋转角 为60°时，箱盖ADE落在AD′E′的位置（如图②所示）．已知AD＝90厘米，DE ＝30厘米，EC＝40厘米. （1）求点D′到BC的距离； （2）求E，E′两点的距离.
解：（1）如解图①，过点D′作D′H⊥BC，垂足为点H，交AD于点F，由题意，得AD′＝AD＝90（厘米），∠DAD′＝60°. ∵四边形ABCD是矩形，∴AD∥BC，∴∠AFD′＝∠BHD′＝90°. 在Rt△AD′F中，D′F＝AD′·sin ∠DAD′＝90×sin 60°＝ （厘米）. 又∵CE＝40厘米，DE＝30厘米，∴FH＝DC＝DE＋CE＝70（厘米），∴D′H＝D′F＋FH＝（ ＋70）厘米. 答：点D′到BC的距离为（ ＋70）厘米；
（2）连接AE，AE′，EE′，如解图②，由题意，得AE′＝AE，∠EAE′＝60°，∴△AEE′是等边三角形，∴EE′＝AE. ∵四边形ABCD是矩形，∴∠ADE＝90°. 在Rt△ADE中，AD＝90厘米，DE＝30厘米，∴AE＝ （厘米），∴EE′＝ （厘米）.答：E，E′两点的距离是 厘米．
6.（2020南昌一模）如图①，是某保温杯的实物图和平面抽象示意图，点A，B是 保温杯上两个固定点，与两活动环相连，把手CD与两个活动环AD，BC相连， 现测得AD＝BC＝2.6 cm，AB＝17 cm，如图②，当A，D，C三点共线时，恰好 AC⊥BC. （1）求把手CD的长； （2）如图③，当CD∥AB时， 求∠ADC的度数．（参考 数据：sin57.5°≈0.843， cs57.5°≈0.538，tan57.5°≈1.570）
解：（1）∵在Rt△ABC中，∠C＝90°，∴AC＝ （cm），∴CD＝AC－AD＝16.8－2.6＝14.2（cm）；
（2）如解图，分别过C，D作CE⊥AB于点E，DF⊥AB于点F.∵CD∥AB，∴∠CDF＝∠DFE＝∠CEF＝90°，∴四边形CDFE是矩形，∴DF＝CE，EF＝CD.又∵AD＝BC，∴△ADF≌△BCE（HL），∴AF＝BE＝ （AB－EF）＝ ×（17－14.2）＝1.4（cm），∴cs ∠DAF＝ ≈0.538，∴∠DAF＝57.5°.∵CD∥AB，∴∠ADC＝180°－∠DAF＝122.5°.
7.（2019江西样卷）图①是一个家用花架，将实物图的主体部分抽象成图②.花架 接口处可活动，如图③，将实物图的主体部分抽象成图④.ER＝CQ＝60 cm， 点K，H，N，M分别是RE，CQ的三等分点，SC＝HT＝PN＝RZ＝45 cm，RQ＝ KN＝HM＝EC＝DE＝15 cm，AB＝30 cm，RZ∥PN∥HT∥SC∥AB， AD∥ER∥BQ，且AD＝40 cm，花架移轮直径为6 cm，在图④中∠RES＝60°. （1）根据四边形的 ，图①能变形到图③，在图④中为了稳定花架， 在花架底部可以固定一根木条，其理由是 ． （2）在图④中连接RS，ZC，求证：四边形RSCZ是矩形. （3）一盆吊兰从盆底垂下的长度为50 cm，在图④中，判断：吊兰至少应放在花 架哪一层，才不会接触到地面？（ ≈1.732）
（1）解：不稳定性；三角形具有稳定性；（2）证明：如解图，连接RS，ZC，过点S作SJ⊥ER于点J.在Rt△SEJ中，∠RES＝60°，SE＝SC－EC＝45－15＝30（cm），∴EJ＝15 cm，SJ＝ （cm）.∵RE＝60 cm，∴RJ＝60－15＝45（cm）.在Rt△SRJ中，tan ∠SRE＝ ，∴∠SRE＝30°，∴∠RES＋∠SRE＝90°，∴∠RSE＝90°.∵RZ∥SC，SC＝RZ，∴四边形RSCZ为矩形；
（3）解：∵一盆吊兰从盆底垂下的长度为50 cm，MB＝MC＋BC＝ QC＋DA＝60 （cm），如解图，连接MA，由（2）可证∠MAB＝90°.在Rt△MAB中，∠MBA＝∠RES＝60°，∴MA＝MB·sin ∠MBA＝60× （cm）.∴点M到地面的距离为（ ＋6）cm≈57.96 cm>50 cm，答：吊兰至少应放在花架MT层，才不会接触到地面．
类型3　圆模型（2013）
1.（2013江西21题9分）如图①，一辆汽车的背面，有一种特殊形状的刮雨器， 忽略刮雨器的宽度可抽象为一条折线OAB，如图②所示，量得连杆OA长为 10cm，雨刮杆AB长为48 cm，∠OAB＝120°. 若启动一次刮雨器，雨刮杆AB 正好扫到水平线CD的位置，如图③所示. （1）求雨刮杆AB旋转的最大角度及O，B两点之间的距离；（结果精确到0.01） （2）求雨刮杆AB扫过的最大面积．（结果保留π的整数倍）（参考数据：sin60°＝ ，cs60°＝ ，tan60°＝ ， ≈26.851，可使用科学计算器）
解：（1）A点转到C点，B点转到D点，启动一次刮雨器，雨刮杆AB正好扫到水平线CD的位置，故雨刮杆AB旋转的最大角度为180°.过点O作OE⊥BA，交BA延长线于点E，连接BO，如解图①，∵∠OAB＝120°，∴∠OAE＝60°，∴∠EOA＝30°.∵OA长为10 cm，∴EA＝ OA＝5（cm），∴EO＝ （cm）.∵AB＝48 cm，∴EB＝48＋5＝53(cm)，∴BO＝ ≈53.70（cm）.答：雨刮杆AB旋转的最大角度为180°，O、B两点之间的距离约为53.70 cm；
（2）如解图②，∵雨刮杆AB旋转180°得到CD，即△OCD与△OAB关于点O中心对称，∴△BAO≌△DCO，∴S△BAO＝S△DCO，∴雨刮杆AB扫过的最大面积S＝ π（OB2－OA2）＝1 392π（cm2）. 答：雨刮杆AB扫过的最大面积为1 392π cm2.
2.（原创推荐）某幼儿园中，将小朋友玩的呼啦圈放在一个槽内，其主视图如图 ①所示，将其抽象为平面图形如图②所示，矩形ACDB的边CD与⊙O相切于 点E，测得∠EAC＝58°，呼啦圈的半径为40 cm（忽略呼啦圈的宽度）. （1）求呼啦圈放置槽的深度AC；（结果保留1位小数） （2）求呼啦圈在放置槽中部分的长度（阴影部 分的弧长）.（结果保留1位小数．参考数 据：sin58°≈0.85，cs58°≈0.53， tan58°≈1.60，π≈3.14）
解：（1）如解图，连接OA，OE，过点O作OF⊥AE于点F，则AE＝2EF，∠OEF＝∠EAC＝58°.在Rt△OEF中，EF＝OE·cs58°≈21.2（cm），∴AE≈42.4（cm），在Rt△ACE中，可得AC＝AE·cs58°≈22.5（cm）.答：呼啦圈放置槽的深度AC约为22.5 cm；（2）∵∠OAE＝∠OEF＝58°，∴∠AOE＝64°.如解图，连接OB，可得∠AOB＝128°，∴ （cm）.答：呼啦圈在放置槽中部分的长度约为89.3 cm.
3.（2020连云港节选）筒车是我国古代利用水力驱动的灌溉工具，唐代陈廷章在 《水轮赋》中写道：“水能利物，轮乃曲成”．如图，半径为3 m的筒车⊙O按逆 时针方向每分钟转 圈，筒车与水面分别交于点A、B，筒车的轴心O距离水 面的高度OC长为2.2 m，筒车上均匀分布着若干个盛水筒．若以某个盛水筒P 刚浮出水面时开始计算时间． （1）经过多长时间，盛水筒P首次到达最高点？ （2）若接水槽MN所在直线是⊙O的切线，且与直线AB交于点M，MO＝ 8 m．求盛水筒P从最高点开始，至少经过多长时间恰好在直线MN上．（参考数据：cs43°＝sin47°≈ ，sin16°＝cs74°≈ ，sin22°＝cs68°≈ ）
解：（1）如解图①，连接OA.由题意，筒车每秒旋转360°× ÷60＝5°，在Rt△ACO中，cs ∠AOC＝ .∴∠AOC≈43°，∴ ＝27.4（秒）.答：经过27.4秒，盛水筒P首次到达最高点；
（2）如解图②，∵点P在⊙O上，且MN与⊙O相切，∴当点P在MN上时，此时点P是切点，连接OP，则OP⊥MN，延长CO交⊙O于点H.在Rt△OPM中，cs ∠POM＝ ，∴∠POM≈68°，在Rt△COM中，cs ∠COM＝ ，∴∠COM≈74°，∴∠POH＝180°－∠POM－∠COM≈180°－68°－74°＝38°，∴需要的时间为 ＝7.6（秒）.答：盛水筒P从最高点开始，至少经过7.6秒恰好在直线MN上．
4.（2020江西省模拟）如图是一个桌面会议话筒示意图，中间BC部分是一段可 弯曲的软管，在弯曲时可形成一段圆弧，设圆弧所在圆的圆心为O，线段AB ， CD均与圆弧相切，点B，C分别为切点，已知AB的长为10 cm，CD的长为 25.2 cm. （1）如图①，若话筒弯曲后CD与桌面AM平行，此时CD距离桌面14 cm，求弧 BC的长度（结果保留π）； （2）如图②，若话筒弯曲后弧BC所对的圆心角度数为60°，求话筒顶端D到 桌面AM的距离（结果保留一位小数）.（参考数据： ≈1.73）
解：（1）∵线段AB，CD均与圆弧相切，∴OB⊥AB，OC⊥CD，∴CD∥OB∥AM，∴∠BOC＝∠OCD＝90°.∵CD距离桌面14 cm，AB的长为10 cm，∴半径OC为4 cm.∴弧BC的长度为 ＝2π（cm）.即弧BC的长度为2π cm；
（2）如解图，过点C作CN⊥DM于点N，设BO的延长线与DM交于点H，过点C作CG⊥OB于点G.易得四边形CGHN是矩形，∴CN∥OB，CG＝NH.∴∠OCN＝∠BOC＝60°.∵∠OCD＝90°，∴∠NCD＝30°，∴DN＝ CD＝ ×25.2＝12.6（cm）.∵弧BC的长度为2π cm，∴2π＝ .∴OB＝OC＝6（cm），∴CG＝OC·sin 60°＝6× ≈5.2（cm），∴DM＝DN＋CG＋AB＝12.6＋5.2＋10＝27.8（cm）．答：话筒顶端D到桌面AM的距离是27.8 cm.