初中数学8 图形的位似优秀课时练习

这是一份初中数学8 图形的位似优秀课时练习，共19页。试卷主要包含了在平面直角坐标系中，已知点A等内容，欢迎下载使用。

2021-2022学年北师大版九年级数学上册《4.8图形的位似》同步达标测评（附答案）
一．选择题（共8小题，满分32分）
1．如图，在△AOB中，A，B两点在x轴的上方，以点O为位似中心，在x轴的下方按1：2的相似比作△AOB的位似图形△A'OB'．设点B的对应点B'的坐标是（4，﹣2），则点B的坐标是（　　）

A．（2，1） B．（2，﹣1） C．（﹣2，1） D．（﹣2，﹣1）
2．如图，△ABO缩小后变为△A'B'O，其中A、B的对应点分别为A'、B'，点A、B、A'、B'均在格点上，若线段AB上有点P（m，n），则点P在A'B'上的对应点P'的坐标为（　　）

A．（，n） B．（m，n） C．（m，） D．（）
3．如图，在平面直角坐标系中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且面积比为1：9，点A、B、E点在x轴上，若点D的坐标为（1，2），则点G的坐标为（　　）

A．（3，6） B．（4，8） C．（6，12） D．（6，10）

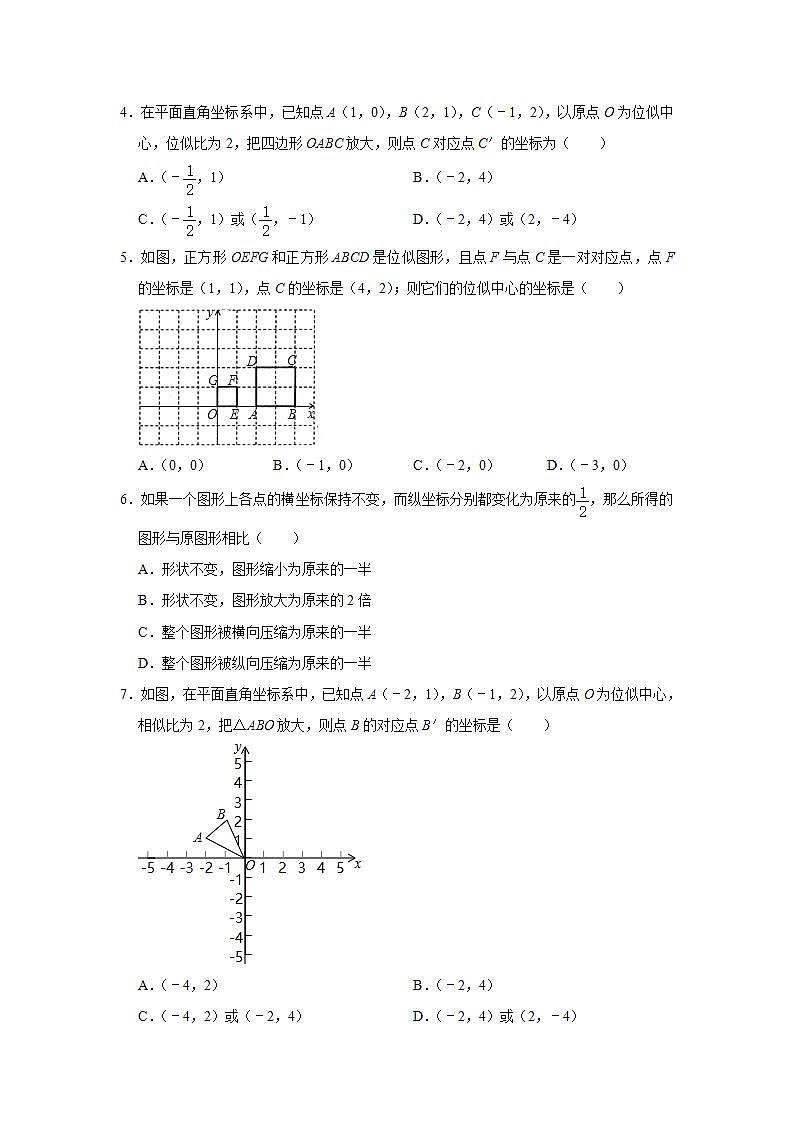
4．在平面直角坐标系中，已知点A（1，0），B（2，1），C（﹣1，2），以原点O为位似中心，位似比为2，把四边形OABC放大，则点C对应点C′的坐标为（　　）
A．（﹣，1） B．（﹣2，4）
C．（﹣，1）或（，﹣1） D．（﹣2，4）或（2，﹣4）
5．如图，正方形OEFG和正方形ABCD是位似图形，且点F与点C是一对对应点，点F的坐标是（1，1），点C的坐标是（4，2）；则它们的位似中心的坐标是（　　）

A．（0，0） B．（﹣1，0） C．（﹣2，0） D．（﹣3，0）
6．如果一个图形上各点的横坐标保持不变，而纵坐标分别都变化为原来的，那么所得的图形与原图形相比（　　）
A．形状不变，图形缩小为原来的一半
B．形状不变，图形放大为原来的2倍
C．整个图形被横向压缩为原来的一半
D．整个图形被纵向压缩为原来的一半
7．如图，在平面直角坐标系中，已知点A（﹣2，1），B（﹣1，2），以原点O为位似中心，相似比为2，把△ABO放大，则点B的对应点B′的坐标是（　　）

A．（﹣4，2） B．（﹣2，4）
C．（﹣4，2）或（﹣2，4） D．（﹣2，4）或（2，﹣4）
8．如图，△ABC中，A，B两个顶点在x轴的上方，点C的坐标是（﹣1，0）．以点C为位似中心，在x轴的下方作△ABC的位似图形，并把△ABC的边长放大到原来的2倍，记所得的像是△A′B′C．设点B的对应点B′的横坐标是a，则点B的横坐标是（　　）

A． B． C． D．
二．填空题（共13小题，满分52分）
9．如图，△ABC与△A′B′C′是位似图形，点O是位似中心，若OA＝2AA′，S△ABC＝9，则S△A'B'C′＝　 　．

10．若将一个正方形的各边长扩大为原来的4倍，则这个正方形的面积扩大为原来的 　 　倍．
11．如图，已知，直角坐标系中，点E（﹣4，2），F（﹣1，﹣1），以O为位似中心，按比例尺2：1把△EFO缩小，则点E的对应点E′的坐标为　 　．

12．如图，在平面直角坐标系中，正方形OABC与正方形ODEF是位似图形，点O为位似中心．位似比为2：3，点B、E在第一象限，若点A的坐标为（1，0），则点E的坐标是　 　．

13．如图，在平面直角坐标系中，正方形OABC和正方形ADEF的边OA、AD分别在x轴上，OA＝2，AD＝3，则正方形OABC和正方形ADEF位似中心的坐标是　 　．

14．在如图所示的格点图中，每个小正方形的边长都是1，以点O为位似的中心，画出△A'B′C′，使△ABC与△A′B'C′的相似比为1：2，则点C′的坐标为　 　．

15．如图，△OAB与△OCD是以点O为位似中心的位似图形，相似比为3：4，∠OCD＝90°，∠AOB＝60°，若点B的坐标是（6，0），则点C的坐标是　 　．

16．如图，在平面直角坐标系xOy中，△ABC与△A′B′C′的顶点的横、纵坐标都是整数．若B（5，2），△ABC与△A′B′C′是位似图形，则位似中心的坐标是　 　．

17．如图，正方形OABC和正方形DEFG是位似图形，点B坐标为（﹣1，1），点F坐标为（4，2），且位似中心在这两个图形的同侧，则位似中心的坐标为　 　．

18．如图，在平行四边形ABCD中，F是AD延长线上一点，连接BF分别交AC、CD于P、E，则图中的位似三角形共有　 　对．

19．如图，矩形OABC与矩形ODEF是位似图形，P是位似中心，点B（4，2），E（﹣2，1），则点P的坐标为　 　．

20．如图，正方形OEFG和正方形ABCD是位似形，点F的坐标为（1，1），点C的坐标为（4，2），则这两个正方形位似中心的坐标是　 　．

21．如图，正方形ABCD和正方形OEFG中，点A和点F的坐标分别为（3，2），（﹣1，﹣1），则两个正方形的位似中心的坐标是　 　，　 　．

三．解答题（共5小题，满分36分）
22．如图，△ABC在坐标平面内，三个顶点的坐标分别为A（0，2），B（2，2），C（4，4）（正方形网格中，每个小正方形的边长为1）．
（1）画出△ABC关于x轴的对称图形△A1B1C1，并写出点B1的坐标．
（2）以点O为位似中心，在第三象限画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为1：2．



23．如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别为A（﹣1，2），B（﹣3，4），C（﹣2，6）．
（1）画出△ABC绕点A顺时针旋转90°后得到的△A1B1C1，写出点C1的坐标．
（2）以原点O为位似中心，画出将△A1B1C1三条边放大为原来的2倍后得△A2B2C2，写出点B2的坐标．


24．如图，在边长为1个单位长度的小正方形组成的网格中，建立如图所示的平面直角坐标系，并给出了格点△ABC（顶点为网格线的交点）．
（1）画出△ABC关于y轴对称的△A1B1C1；
（2）以点O为位似中心，将△ABC作位似变换得到△A2B2C2，使得A2B2＝2AB，画出位似变换后的△A2B2C2；
（3）A1C1和B2C2之间的位置关系为 　 　．



25．如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，3），B（4，1），C（1，1）．
请解答下列问题：
（1）画出△ABC关于x轴成轴对称的△A1B1C1，并直接写出点B1的坐标；
（2）以原点O为位似中心，位似比为1：2，在y轴的左侧，画出△A1B1C1放大后的图形△A2B2C2，并直接写出A2点的坐标．



26．如图，在平面直角坐标系中，△ABC三个顶点的坐标分别为A（1，1）、B（4，2）、C（3，5）．
（1）请画出△ABC关于x轴的对称图形△A1B1C1；
（2）以0为位似中心，在第三象限内画出△ABC的位似图形△A2B2C2，且位似比为1；
（3）借助网格，利用无刻度直尺画出线段CD，使CD平分△ABC的面积．（保留确定点D的痕迹）


参考答案
一．选择题（共8小题，满分32分）
1．解：设点B的坐标为（x，y），
因为点B的对应点B'的坐标是（4，﹣2），
所以根据位似变换的坐标特点得﹣2•x＝4，﹣2•y＝﹣2，
即x＝﹣2，y＝1，故点B的坐标为（﹣2，1）．
故选：C．
2．解：∵△ABO缩小后变为△A′B′O，其中A、B的对应点分别为A′、B′点A、B、A′、B′均在图中在格点上，
即A点坐标为：（4，6），B点坐标为：（6，2），A′点坐标为：（2，3），B′点坐标为：（3，1），
∴线段AB上有一点P（m，n），则点P在A′B′上的对应点P′的坐标为：（）．
故选：D．
3．解：∵正方形ABCD中的点D的坐标为（1，2），
∴OA＝1，AB＝2．
∴OB＝3
∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且面积比为1：9，即相似比为1：3，
∴△OBC∽△OEF，且＝，
∴＝＝，
∴＝，即＝
解得，BE＝6，
∴点G的坐标为（3，6），
故选：A．
4．解：∵点A（1，0），B（2，1），C（﹣1，2），以原点O为位似中心，位似比为2，把四边形OABC放大，
∴点C对应点C′的坐标为：（﹣2，4）或（2，﹣4）．
故选：D．
5．解：∵点F与点C是一对对应点，可知两个位似图形在位似中心同旁，位似中心就是CF与x轴的交点，
设直线CF解析式为y＝kx+b，
将C（4，2），F（1，1）代入，
得，
解得 ，
即y＝x+，
令y＝0得x＝﹣2，
∴O′坐标是（﹣2，0）；
故选：C．
6．解：∵一个图形上各点的横坐标保持不变，而纵坐标分别都变化为原来的，
∴整个图形被纵向压缩为原来的一半
故选：D．
7．解：∵以原点O为位似中心，相似比为2，将△OAB放大为△OA′B′，点B（﹣1，2），
∴B′点的坐标为（﹣2，4）或（2，﹣4）．
故选：D．
8．解：过B点和B′点作x轴的垂线，垂足分别是D和E
∵点B′的横坐标是a，点C的坐标是（﹣1，0）．
∴EC＝a+1
又∵△A′B′C的边长是△ABC的边长的2倍
∴DC＝（a+1）
∴DO＝（a+3）
∴B点的横坐标是
故选：D．

二．填空题（共13小题，满分52分）
9．解：△ABC与△A′B′C′是位似图形且由OA＝2AA′．
可得两位似图形的位似比为2：3，所以两位似图形的面积比为4：9，
又S△ABC＝9，
∴S△A'B'C′＝．
故答案为：．
10．解：根据正方形面积的计算方法和积的变化规律，如果一个正方形的边长扩大为原来的4倍，那么正方形的面积是原来正方形面积的4×4＝16倍．
故答案为：16．
11．解：如图所示：∵E（﹣4，2），F（﹣1，﹣1），以O为位似中心，按比例尺2：1，把△EFO缩小，
∴点E的对应点E′的坐标为：（﹣2，1）或（2，﹣1）．
故答案为：（﹣2，1）或（2，﹣1）．

12．解：∵正方形OABC与正方形ODEF是位似图形，O为位似中心，相似比为2：3，
∴OA：OD＝2：3，
∵点A的坐标为（1，0），
即OA＝1，
∴OD＝，
∵四边形ODEF是正方形，
∴DE＝OD＝．
∴E点的坐标为：（，）．
故答案是：（，）．
13．解：连接FC并延长交x轴于点M，
由题意可得：△MOC∽△MAF，
则＝＝，
∴＝，
解得：MO＝4，
故M点的坐标为：（﹣4，0）．
连接DC，OE，交点为N，
可得△CNO∽△END，
则＝＝，
解得：AN＝，
故N点坐标为：（2，），
综上所述：正方形OABC和正方形ADEF位似中心的坐标是（﹣4，0）或（2，）．
故答案为：（﹣4，0）或（2，）．

14．解：如图所示，满足条件的三角形有两个：△A′B′C′．

观察图象可知：点C′的坐标为（10，﹣4）．
故答案为：（10，﹣4）
15．解：分别过A、C作AE⊥OB，CF⊥OB，
∵∠OCD＝90°，∠AOB＝60°，
∴∠ABO＝∠CDO＝30°，∠OCF＝30°，
∵△OAB与△OCD是以点O为位似中心的位似图形，相似比为3：4，点B的坐标是（6，0），
∴D（8，0），则DO＝8，
故OC＝4，
则FO＝2，CF＝CO•cos30°＝4×＝2，
故点C的坐标是：（2，2）．
故答案为：（2，2）．

16．解：直线AA′与直线BB′的交点坐标为（8，0），
所以位似中心的坐标为（8，0）．
故答案为：（8，0）

17．解：作直线BG交x轴于点M，
∵点B坐标为（﹣1，1），点F坐标为（4，2），
∴AB＝1，GD＝2，AD＝1+2＝3，
∵正方形OABC和正方形DEFG是位似图形，
∴AB∥GD，
∴，
∴，
∴MA＝3，
∴OM＝MA+OA＝4，
∴M（﹣4，0），
故答案为：（﹣4，0）．

18．解：∵四边形ABCD是平行四边形
∴AD∥BC，AB∥CD，
∴△ABP∽△CEP，△APF∽△CPB，△DEF∽△CEB，△DEF∽△ABF，
∴△ABF∽△CEB，△ABC≌△CDA
∴此图中共有6对相似三角形．
故答案为6
19．解：∵矩形OABC与矩形ODEF是位似图形，P是位似中心，点B（4，2），E（﹣2，1），
∴D（0，1），B（4，2），
∴＝，
则＝，
解得：OP＝4，
则点P的坐标为：（﹣4，0）．
故答案为：（﹣4，0）．
20．解：两个图形位似时，①位似中心就是CF与x轴的交点，
设直线CF解析式为y＝kx+b，将C（4，2），F（1，1）代入，得
，解得，即y＝x+，
令y＝0得x＝﹣2，
∴O′坐标是（﹣2，0）．
②OC和BG的交点也是位似中心，
直线BG的解析式为y＝﹣x+1，直线OC的解析式为y＝x，
由解得，
∴位似中心的坐标（，），
故答案为（﹣2，0）或（，）．

21．解：∵正方形ABCD和正方形OEFG中A和点F的坐标分别为（3，2），（﹣1，﹣1），
∴E（﹣1，0）、G（0，﹣1）、D（5，2）、B（3，0）、C（5，0），
（1）当E和C是对应顶点，G和A是对应顶点时，位似中心就是EC与AG的交点，
设AG所在直线的解析式为y＝kx+b（k≠0），
∴，解得．
∴此函数的解析式为y＝x﹣1，与EC的交点坐标是（1，0）；
（2）当A和E是对应顶点，C和G是对应顶点时，位似中心就是AE与CG的交点，
设AE所在直线的解析式为y＝kx+b（k≠0），
，解得，故此一次函数的解析式为y＝x+…①，
同理，设CG所在直线的解析式为y＝kx+b（k≠0），
，解得，
故此直线的解析式为y＝x﹣1…②
联立①②得
解得，故AE与CG的交点坐标是（﹣5，﹣2）．
故答案为：（1，0）、（﹣5，﹣2）．
三．解答题（共5小题，满分36分）
22．解：（1）如图，△A1B1C1为所作，点B1的坐标为（2，﹣2）；

（2）如图，△A2B2C2为所作．
23．解：（1）如图，△A1B1C1为所求作的三角形，C1（3，3）．

（2）如图所示，则△A2B2C2为所求作的三角形，B2（2，8）．
24．解：（1）如图，△A1B1C1即为所求．

（2）如图，△A2B2C2即为所求．
（3）A1C1∥B2C2或平行．
故答案为：A1C1∥B2C2或平行．
25．解：（1）如图所示，△A1B1C1即为所求，B1（4，﹣1）；
（2）如图所示，△A2B2C2即为所求，A2（﹣2，6）．

26．解：（1）如图所示：△A1B1C1即为所求；

（2）如图所示：△A2B2C2即为所求；
（3）如图所示：CD即为所求．