初中北师大版8 图形的位似试讲课ppt课件

第2课时 平面直角坐标系中的位似变换

【知识与技能】

1.理解位似图形的定义，能熟练地利用坐标变化将一个图形放大与缩小.

2.理解平移、轴对称、旋转和位似四种变换的基本性质，会按要求画出经变换后的图形.

【过程与方法】

在具体活动操作中，培养学生的动手操作能力，进一步增强用位似变换来解决实际问题的能力.

【情感态度】在观察、操作、推理、归纳等探索过程中，进一步培养学生综合运用知识的能力，体验成功的喜悦，树立良好的数学自信心.

【教学重点】

用图形的坐标变化来表示图形的位似变换，能综合运用平移、轴对称、旋转和位似进行图案设计.

【教学难点】

体会用图形的坐标变化来表示图形的位似变换的变化规律.

一、情境导入，初步认识

问题 如图，已知点A（0，3），B（2，0）是平面直角坐标系内的两点，连接AB.

（1）将线段AB向左平移3个单位得到线段A1B1，画出图形，并写出A1，B1的坐标；

（2）作出线段AB关于y轴对称的线段A2B2，并写出A2，B2点的坐标；

（3）将线段AB绕原点O旋转180°得到线段A3B3，画出图形，并写出A3，B3的坐标.

（4）以原点O为位似中心，位似比为，把线段AB缩小，得到线段A4B4，请在图中画出线段A4B4，写出A4，B4坐标.观察对应点坐标的变化，你有什么发现？

【教学说明】问题（1）、（2）、（3），从学生已有的知识入手，以问题为载体，自然复习平移、轴对称、旋转等变换.而问题（4），则是承上启下为新课的学习做好铺垫，同时，与问题（1）、（2）、（3）一起形成了完整的知识结构，这样以旧引新，帮助学生建立新旧知识间的联系.对问题（1）、（2）、（3）的处理，可采用灵活多样形式，既可自主探究，也可小组讨论相互交流，教师也可适时参与讨论.在处理问题（4）时，教师可给学生充裕的探讨时间，让学生自己发现结论.

二、思考探究，获取新知

通过上面的问题（4）思考，可以发现：在平面直角坐标系中，如果位似是以原点为位似中心，位似比为k，那么位似图形对应点坐标的比为k或-k.这一结论是否正确呢？下面我们再通过探究来验证一下.

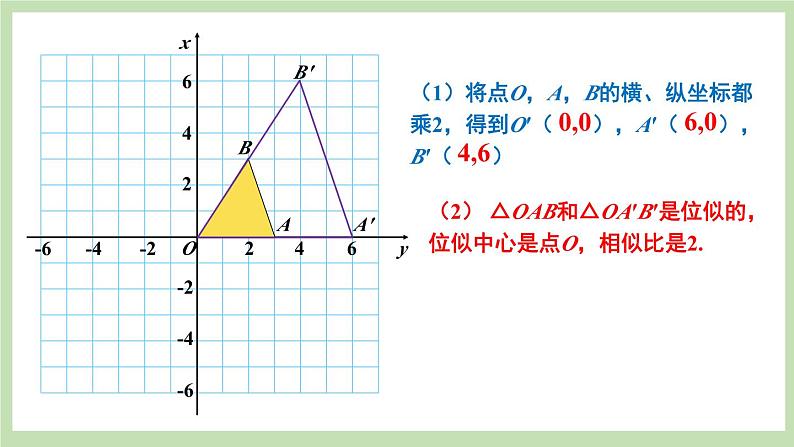
问题 如图，△ABC三个顶点坐标分别为A（2，3），B（2，1），C（4，3），以点O为位似中心，相似比为2，将△ABC放大，得到△A1B1C1.

（1）请在图中画出所有满足要求的△A1B1C1;

（2）写出A、B、C的对应点A1，B1，C1的坐标；

（3）观察对应顶点坐标的变化，你有什么发现？

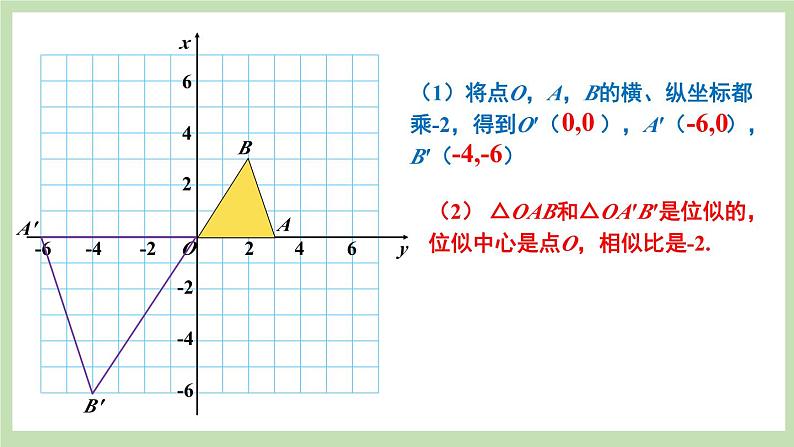
分析与解 （1）作直线OA，OB，OC，在射线OA、OB、OC上，截取A1，B1，C1，使，依次连接A1，B1，C1，得△A1B1C1，则△A1B1C1是适合要求的图形；类似地，在第三象限可画△A2B2C2，使得△A2B2C2是以O为位似中心，位似比为2的放大图形，如图所示：

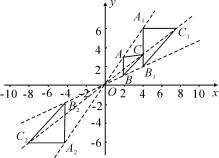
（2）把△ABC放大后，A，B，C的对应点为A1（4，6），B1（4，2），C1（8，6）；A2（-4，-6），B2（-4，-2），C2（-8，-6）；

（3）观察对应点坐标的变化，可以发现，各顶点的横、纵坐标均是其对应点横、纵坐标的k倍或-k倍.

【教学说明】通过对上述问题的探究思考，让学生主动参与数学知识的“再发现”，在动手——猜想——交流——归纳过程中进一步体验坐标平面内的位似变换性质.

性质 在平面直角坐标系中，如果位似是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比为k或-k.

三、典例精析，掌握新知

例1 △OEF是△OAB以点O为位似中心；由△OAB放大而得到的，若点A、B坐标分别为（-1，4）和（3，2），且相似比为3∶1，求点E、F的坐标.

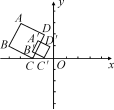分析与解 由坐标平面内以原点O为位似中心的两个图形的对应顶点坐标之间的关系可以知道，点E，F的坐标应为（-1×3，4×3）和（3×3，2×3）或（-1×（-3），4×（-3））和（3×（-3），2×（-3）），即E、F的坐标为（-3，12）和（9，6）或（3，-12）和（-9，-6）.

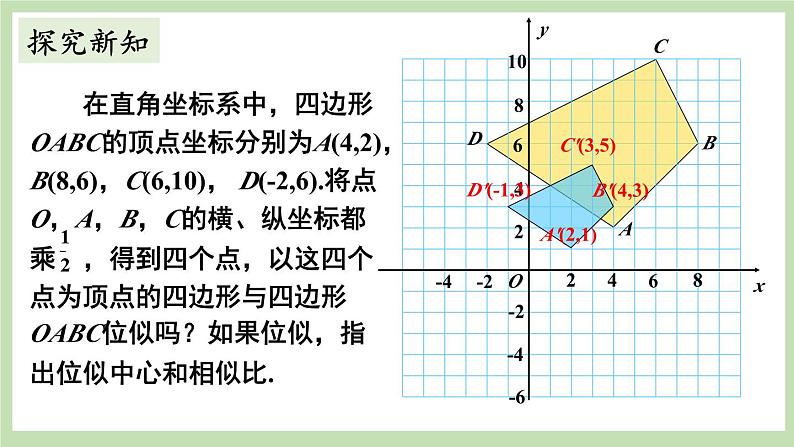
例2 如图，四边形ABCD的坐标分别为A（-6，6），B（-8，2），C（-4，0），D（-2，4），画出它的一个以原点O为位似中心，相似比为的位似图形.

分析与解 问题的关键是要确定位似图形各个顶点的坐标.根据前面的规律，点A的对应点A′的坐标为（-6×，6×），即（-3，3）.类似地，可以确定其他顶点的坐标.

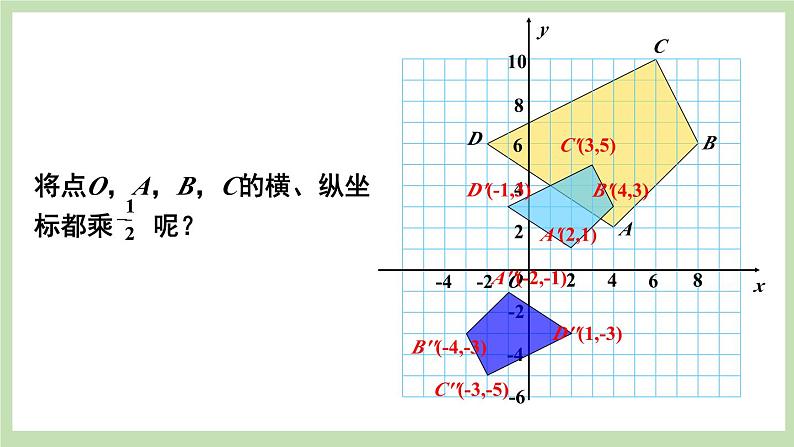
如图，利用位似中对应点的坐标的变化规律，分别取A′（-3，3），B′（-4，1），C（-2，0），D′（-1，2）.依次连接A′，B′，C′，D′，四边形A′B′C′D′就是要求的四边形ABCD的位似图形.

【教学说明】这里的两道题都可让学生自主探究，教师巡视，发现问题及时指导，最后教师再展示解题过程，锻炼学生的解题能力.在例2中，还可以画出四边形ABCD类似原点O在第四象限的位似图形，可让学生试一试.

四、运用新知，深化理解

1.如图表示△AOB和把它缩小后得到的△OCD，求△AOB与△COD的相似比.

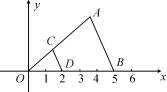
2.如图，△ABC三个顶点坐标分别为A（2，-2），B（4，-5），C（5，-2），以原点O为位似中心，将这个三角形放大为原来的2倍.

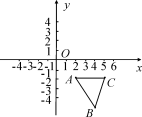
【教学说明】 所选的两道题是前面知识的延续，学生可自主完成，教师巡视，对优秀者应给予鼓励，增强他们学习兴趣.

五、师生互动，课堂小结

1.通过本节课的学习，你有哪些收获？

2.列举出生活中的位似图案.

【教学说明】 针对问题1，学生可发表各自看法，这样一方面可提炼本节知识点，另一方面也可对所存在的问题进行探讨，完善知识技能.而问题2则可让学生感受数学来源于生活，从而更深理解本节知识.

1.布置作业：从教材P51习题27.3中选取.

2.完成练习册中相应练习.

本课时可类比上一课时的教学方式进行，只不过本课时涉及到了平面直角坐标系，教学时教师应让学生充分参与，体会平面直角坐标系中的位似变换，以培养学生的动手操作能力和用位似变换解决实际问题的能力.本课的难点是用图形的坐标变化来表示图形的位似变换的变化规律，教师可让学生以小组为单位进行讨论，争取让学生自己发现规律，教师再予以适当点拨，以培养学生的探究能力.