
2021学年第2章 对称图形——圆综合与测试复习练习题
展开第2章《对称图形--圆》单元自测卷(1)-苏科版九年级数学上册培优训练
一、选择题(本大题共有8小题,每小题3分,共24分)
1、已知⊙O的直径为10,点P到点O的距离大于8,那么点P的位置( )
A.一定在⊙O的内部 B.一定在⊙O的外部 C.一定在⊙O的上 D.不能确定
2、下列说法:①三角形的外心到三角形三边的距离相等②若两个扇形的圆心角相等,则它们所对的弧长也相等③三点确定一个圆④平分弧的直径垂直于弦⑤等弧所对的圆周角相等⑥在同圆或等圆中,相等的弦所对的弧相等,其中正确的个数有( )
A.0个 B.1个 C.2个 D.3个
3、已知正六边形的边长是2,则该正六边形的边心距是( )
A.1 B. C.2 D.
4、圆锥的高是,其底面圆半径为,则它的侧面展开图的面积为( )
A. B. C. D.
5、如图,半圆的圆心为0,直径AB的长为12,C为半圆上一点,∠CAB=30°,的长是( )
A.12π B.6π C.5π D.4π
(5) (6) (7) (8)
6、如图所示,是的直径,切于点,线段交于点,连接,若,则等于( )
A. B. C. D.
7、如图,在菱形ABCD中,以AB为直径画弧分别交BC于点F,交对角线AC于点E,若AB=4,F为BC的中点,则图中阴影部分的面积为( )
A. B. C. D.
8、如图,已知、两点的坐标分别为、,的圆心坐标为,原点在上,
是上的一动点,则面积的最小值为
A.1 B. C. D.
二、填空题(本大题共有8小题,每小题3分,共24分)
9、的圆心是原点,半径为5,点在上,如果点在第一象限内,那么______.
10、平面直角坐标系内的三个点A(1,-3)、B(0,-3)、C(2,-3),___ 确定一个圆.(填“能”或“不能”)
11、如图,五边形为的内接正五边形,则 .
(11) (12)
12、如图所示,若用半径为6,圆心角为120°的扇形围成一个圆锥的侧面(接缝忽略不计),
则这个圆锥的底面半径是______.
13、⊙O的半径为2,弦BC=2,点A是⊙O上一点,且AB=AC,直线AO与BC交于点D,
则AD的长为_____.
14、在如图所示的网格中,每个小正方形的边长均为1cm,则经过A、B、C三点的弧长是 cm(结果保留π).
(14) (15) (16)
15、如图,⊙C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内弧OB上一点,∠BMO=120°,则⊙C的半径为______.
16、如图,直线,垂足为,点在直线上,,为直线上一动点,若以为半径的与直线相切,则的长为 .
三、解答题(本大题共有11小题,共102分.)
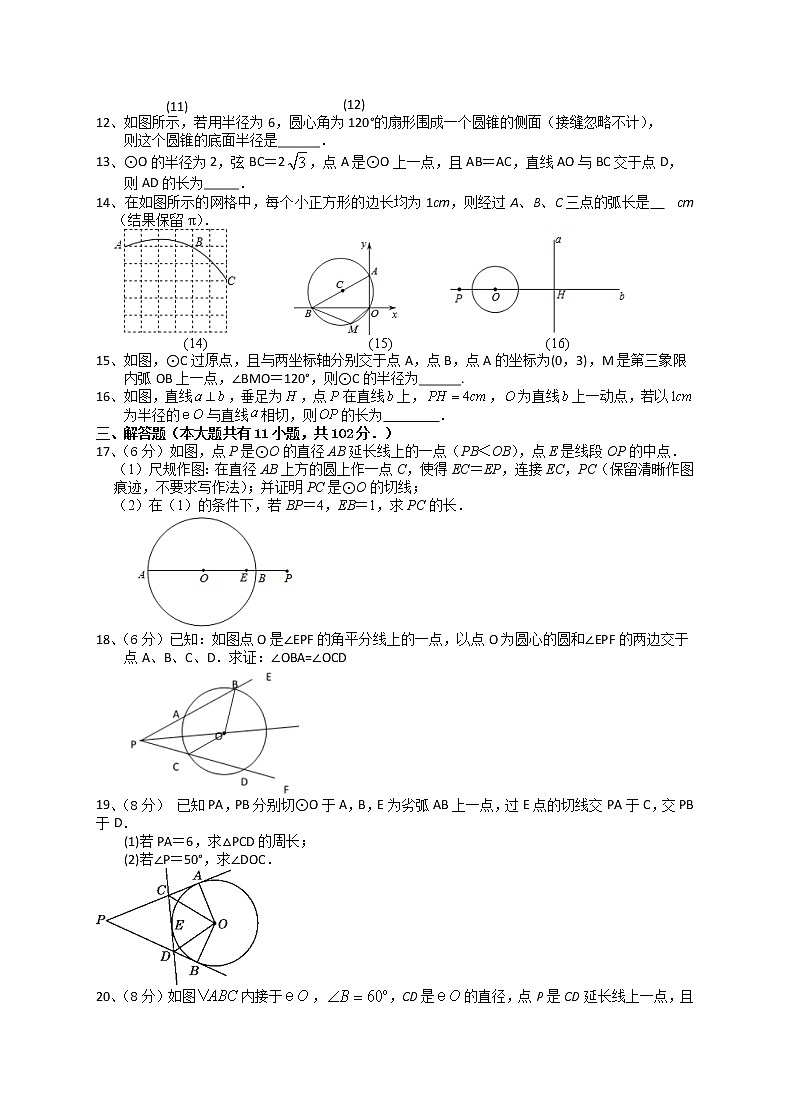
17、(6分)如图,点P是⊙O的直径AB延长线上的一点(PB<OB),点E是线段OP的中点.
(1)尺规作图:在直径AB上方的圆上作一点C,使得EC=EP,连接EC,PC(保留清晰作图痕迹,不要求写作法);并证明PC是⊙O的切线;
(2)在(1)的条件下,若BP=4,EB=1,求PC的长.
18、(6分)已知:如图点O是∠EPF的角平分线上的一点,以点O为圆心的圆和∠EPF的两边交于点A、B、C、D.求证:∠OBA=∠OCD
19、(8分) 已知PA,PB分别切⊙O于A,B,E为劣弧AB上一点,过E点的切线交PA于C,交PB于D.
(1)若PA=6,求△PCD的周长;
(2)若∠P=50°,求∠DOC.
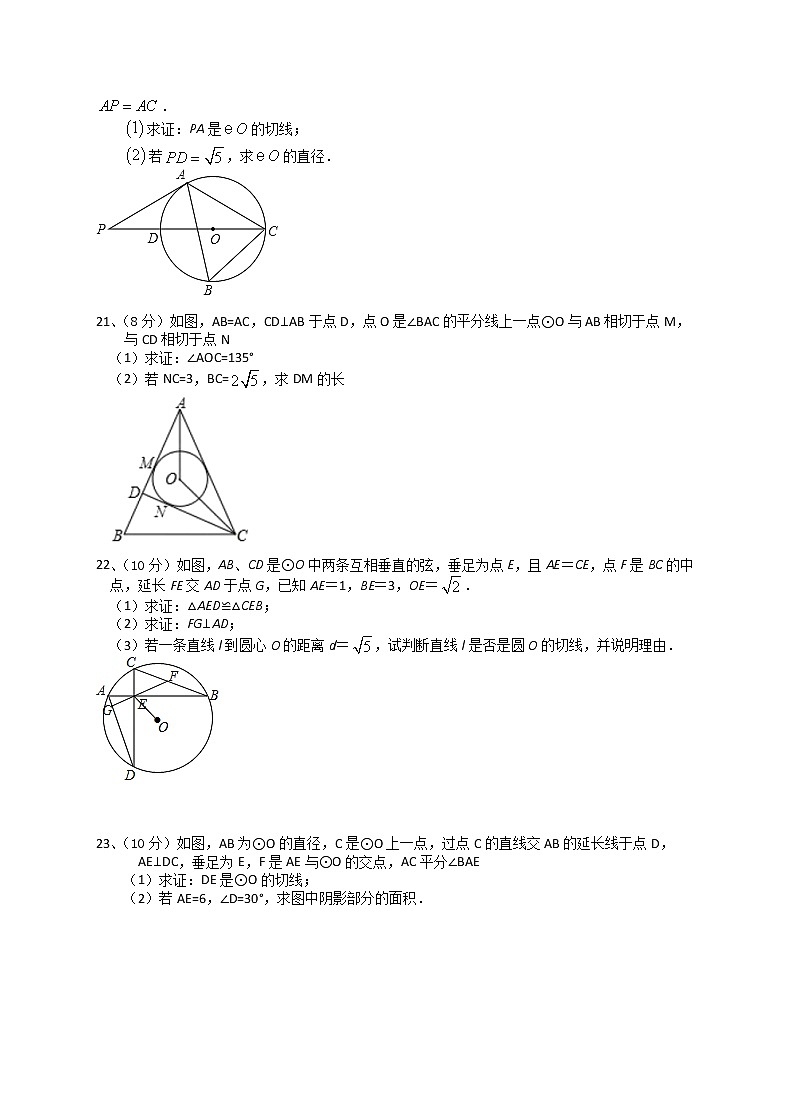
20、(8分)如图内接于,,CD是的直径,点P是CD延长线上一点,且.
求证:PA是的切线;
若,求的直径.
21、(8分)如图,AB=AC,CD⊥AB于点D,点O是∠BAC的平分线上一点⊙O与AB相切于点M,与CD相切于点N
(1)求证:∠AOC=135°
(2)若NC=3,BC=,求DM的长
22、(10分)如图,AB、CD是⊙O中两条互相垂直的弦,垂足为点E,且AE=CE,点F是BC的中点,延长FE交AD于点G,已知AE=1,BE=3,OE=.
(1)求证:△AED≌△CEB;
(2)求证:FG⊥AD;
(3)若一条直线l到圆心O的距离d=,试判断直线l是否是圆O的切线,并说明理由.
23、(10分)如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE
(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
24、(8分)如图,已知是⊙O的直径,点C、D在⊙O上,点E在⊙O外,.
(1)求证:是⊙O的切线;
(2)当时,求阴影部分的面积.
25、(12分)如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作(以下结果保留根号):
(1)利用网格确定该圆弧所在圆的圆心D点的位置,并写出D点的坐标为 ;
(2)连接AD、CD,⊙D的半径为 ,∠ADC的度数为 ;
(3)若扇形DAC是一个圆锥的侧面展开图,求该圆锥底面半径.
26、(12分)如图,在△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A,B,D三点.
(1)求证:AB是⊙O的直径;
(2)判断DE与⊙O的位置关系,并加以证明;
(3)若⊙O的半径为3,∠BAC=60°,求DE的长.
27、(14分)中,,,,点是 的中点,点是直线上方平面内一点(不与、重合),且,以为圆心,为半径作.
(1)如图1,当经过点时,
①为______ 三角形; ②求证:一定经过点; ③阴影部分的面积为______;
(2)如图2,过点作直线于点,且与直线相切,求的长;
(3)设与的另一个交点为,当时,直接写出的长.
第2章《对称图形--圆》单元自测卷(1)-苏科版九年级数学上册 培优训练(解析)
一、选择题(本大题共有8小题,每小题3分,共24分)
1、已知⊙O的直径为10,点P到点O的距离大于8,那么点P的位置( )
A.一定在⊙O的内部 B.一定在⊙O的外部 C.一定在⊙O的上 D.不能确定
试题分析:的直径为10,半径为5,点到点的距离大于8,点一定在的外部,
故选B.
2、下列说法:①三角形的外心到三角形三边的距离相等②若两个扇形的圆心角相等,则它们所对的弧长也相等③三点确定一个圆④平分弧的直径垂直于弦⑤等弧所对的圆周角相等⑥在同圆或等圆中,相等的弦所对的弧相等,其中正确的个数有( )
A.0个 B.1个 C.2个 D.3个
【分析】根据确定圆的条件,垂径定理,三角形外心的性质,圆周角定理,弦、圆心角、弧的关系判断即可.
【答案】解:①三角形的外心到三角形三个顶点的距离相等;故不符合题意;
②在同圆或等圆中,若两个扇形的圆心角相等,则它们所对的弧长也相等,故不符合题意;
③不在同一条直线上的三点确定一个圆,故不符合题意;
④平分弧的直径垂直于这条弧所对的弦;故不符合题意;
⑤等弧所对的圆周角相等,故符合题意;
⑥在同圆或等圆中,相等的弦所对的优弧或劣弧相等,故不符合题意;
故选:B.
3、已知正六边形的边长是2,则该正六边形的边心距是( )
A.1 B. C.2 D.
【分析】正六边形的边长与外接圆的半径相等,构建直角三角形,利用直角三角形的边角关系即可求出.
【详解】如图,连接OA,作OM⊥AB.
∵正六边形ABCDEF的边长为2,∴∠AOM=30°,AMAB2=1,∴正六边形的边心距是OM.
故选B.
4、圆锥的高是,其底面圆半径为,则它的侧面展开图的面积为( )
A. B. C. D.
【答案】C
【分析】利用勾股定理易得圆锥的母线长,圆锥的侧面积=π×底面半径×母线长,把相应数值代入即可求解.
【解析】∵圆锥的高为4cm,底面半径为3cm,
∴圆锥的母线长为:(cm),
∴圆锥的侧面展开图的面积为:π×3×5=15π(cm2).
故选:C.
5、如图,半圆的圆心为0,直径AB的长为12,C为半圆上一点,∠CAB=30°,的长是( )
A.12π B.6π C.5π D.4π
【分析】如图,连接OC,利用等腰三角形的性质及内角和定理求得∠AOC的度数,然后利用弧长公式进行解答即可.
【详解】
解:如图,连接OC,
∵OA=OC,∠CAB=30°,∴∠C=∠CAB=30°,∴∠AOC=120°,
∴弧AC的长度l=.
故选:D.
6、如图所示,是的直径,切于点,线段交于点,连接,若,则等于( )
A. B. C. D.
【分析】直接利用切线的性质得出,再利用三角形内角和定理得出,结合圆周角定理得出答案.
【详解】∵PA切于点A,∴,
∵, ∴,
∴,
故答案为:A.
7、如图,在菱形ABCD中,以AB为直径画弧分别交BC于点F,交对角线AC于点E,若AB=4,F为BC的中点,则图中阴影部分的面积为( )
A. B. C. D.
【分析】取AB的中点O,连接AF,OF,先证明△ABC是等边三角形,再把问题转化为S阴=S扇形OBF,由此即可解决问题.
【详解】解:如图,取AB的中点O,连接AF,OF.
∵AB是直径,∴∠AFB=90°,∴AF⊥BF,∵CF=BF,∴AC=AB,
∵四边形ABCD是菱形,∴AB=BC=AC,∴△ABC是等边三角形,∴AE=EC,
易证△CEF≌△BOF,∴S阴=S扇形OBF==,
故选D.
8、如图,已知、两点的坐标分别为、,的圆心坐标为,原点在上,
是上的一动点,则面积的最小值为
A.1 B. C. D.
解:如图,过点作,交于,此时面积的值最小是定值,只要圆上一点到直线的距离最小,
设直线的解析式为,
,,,,直线的解析式为①,
设直线的解析式为, ,,
,,直线的解析式为②,
联立①②得,,,
,,
的半径为1,,
,,,
,故选:.
二、填空题(本大题共有8小题,每小题3分,共24分)
9、的圆心是原点,半径为5,点在上,如果点在第一象限内,那么______.
【分析】如图,可得OA=5,OB=3,运用勾股定理可以求得AB的长,即为a的值.
【详解】解:如图
由题意得:OA=5,OB=3,
由勾股定理可得:AB=
即a=4
10、平面直角坐标系内的三个点A(1,-3)、B(0,-3)、C(2,-3),___ 确定一个圆.(填“能”或“不能”)
【答案】不能
【分析】根据三个点的坐标特征得到它们共线,于是根据确定圆的条件可判断它们不能确定一个圆.
【解析】解:∵B(0,-3)、C(2,-3),∴BC∥x轴,而点A(1,-3)与C、B共线,
∴点A、B、C共线,∴三个点A(1,-3)、B(0,-3)、C(2,-3)不能确定一个圆.故答案为:不能.
11、如图,五边形为的内接正五边形,则 .
【解答】解:五边形是的内接正五边形,
,,
,
同理,
,
故答案为:.
12、如图所示,若用半径为6,圆心角为120°的扇形围成一个圆锥的侧面(接缝忽略不计),
则这个圆锥的底面半径是______.
【答案】2
【分析】根据半径为6,圆心角为120°的扇形弧长,等于圆锥的底面周长,列方程求解即可.
【解析】设圆锥的底面半径为r,
由题意得,,
解得,r=,
故答案为:.
13、⊙O的半径为2,弦BC=2,点A是⊙O上一点,且AB=AC,直线AO与BC交于点D,
则AD的长为_____.
【分析】根据垂径定理,得AB=AC,AO⊥BC,由勾股定理得OD=1,分两种情况分别求出AD的值,即可
【详解】如图所示:∵⊙O的半径为2,弦BC=2,点A是⊙O上一点,且AB=AC,
∴=,∴AO⊥BC,∴BD=BC=,
在Rt△OBD中,∵BD2+OD2=OB2,即()2+OD2=22,解得OD=1,
∴当如图1所示时,AD=OA﹣OD=2﹣1=1;
当如图2所示时,AD=OA+OD=2+1=3.
故答案为1或3.
14、在如图所示的网格中,每个小正方形的边长均为1cm,则经过A、B、C三点的弧长是 cm(结果保留π).
【分析】先作图确定圆心,然后计算圆心角,最后,再依据弧长公式求解即可.
【解析】连接BC、AB,作BC与AB的垂直平分线交于点O,点O即为A、B、C所在圆的圆心,
则OA2=22+42=20,OA=2
可知∠AOC=90°,
∴过A、B、C三点的弧:
故答案为
15、如图,⊙C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内弧OB上一点,∠BMO=120°,则⊙C的半径为______.
【分析】根据圆内接四边形的对角互补求出∠A的度数,得到∠ABO的度数,根据直角三角形的性质求出AB的长,得到答案.
【详解】解:∵点A的坐标为(0,3),∴OA=3,
∵四边形ABMO是圆内接四边形,
∴∠BMO+∠A=180°,又∠BMO=120°,
∴∠A=60°,则∠ABO=30°,
∴AB=2OA=6,
则则⊙C的半径为3,
故答案为:3.
16、如图,直线,垂足为,点在直线上,,为直线上一动点,若以为半径的与直线相切,则的长为 .
【解答】解:直线,为直线上一动点,
与直线相切时,切点为,
,
当点在点的左侧,与直线相切时,如图1所示:
;
当点在点的右侧,与直线相切时,如图2所示:
;
与直线相切,的长为或,
故答案为:或.
三、解答题(本大题共有11小题,共102分.)
17、(6分)如图,点P是⊙O的直径AB延长线上的一点(PB<OB),点E是线段OP的中点.
(1)尺规作图:在直径AB上方的圆上作一点C,使得EC=EP,连接EC,PC(保留清晰作图痕迹,不要求写作法);并证明PC是⊙O的切线;
(2)在(1)的条件下,若BP=4,EB=1,求PC的长.
【分析】(1)利用尺规作图:以点E为圆心,EP长为半径画弧,在直径AB上方的圆上交一点C,再根据已知条件可得OE=EC=EP,根据三角形内角和可得∠ECO+∠ECP=90°,进而证明PC是⊙O的切线;(2)在(1)的条件下,根据BP=4,EB=1,可得EP的长,进而可得半径,再根据勾股定理即可求PC的长.
【答案】解:(1)如图,点C即为所求;
证明:连接OC,
∵点E是线段OP的中点,
∴OE=EP,
∵EC=EP,
∴OE=EC=EP,
∴∠COE=∠ECO,∠ECP=∠P,
∵∠COE+∠ECO+∠ECP+∠P=180°,
∴∠ECO+∠ECP=90°,
∴OC⊥PC,且OC是⊙O的半径,
∴PC是⊙O的切线;
(2)∵BP=4,EB=1,
∴OE=EP=BP+EB=5,
∴OP=2OE=10,
∴OC=OB=OE+EB=6,
在Rt△OCP中,根据勾股定理,得PC8.
则PC的长为8.
18、(6分)已知:如图点O是∠EPF的角平分线上的一点,以点O为圆心的圆和∠EPF的两边交于点A、B、C、D.求证:∠OBA=∠OCD
【答案】见解析.
【分析】过点O分别作OM⊥AB,ON⊥CD,则可知OM=ON,且OB=OC,则可证得△OMB≌△ONC,可得出∠OBA=∠OCD.
证明: 过点O分别作OM⊥AB,ON⊥CD,垂足分别为M、N
∵∠EPO=∠FPO,∴OM=ON,
在Rt△OMB和Rt△ONC中,,
∴Rt△OMB≌Rt△ONC(HL),∴∠OBA=∠OCD.
19、(8分) 已知PA,PB分别切⊙O于A,B,E为劣弧AB上一点,过E点的切线交PA于C,交PB于D.
(1)若PA=6,求△PCD的周长;
(2)若∠P=50°,求∠DOC.
【答案】(1)△PCD的周长为12;(2)∠DOC=65°.
【分析】
(1) )连接OE,由切线长定理可得PA=PB=6,AC=CE,BD=DE.再由△PCD的周长=PC+PD+CD=PC+PD+CE+DE=PC+PD+AC+BD=PA+PB即可求得△PCD的周长;(2)根据已知条件易求∠AOB=130°;再证明Rt△AOC≌Rt△EOC,由全等三角形的性质可得∠AOC=∠COE.同理可求得∠DOE=∠BOD,由此可得∠DOC=∠AOB=65°.
(1)连接OE,
∵PA,PB与⊙O相切,∴PA=PB=6.
同理可得:AC=CE,BD=DE.
∴△PCD的周长=PC+PD+CD=PC+PD+CE+DE=PC+PD+AC+BD=PA+PB=12.
(2)∵PA,PB与⊙O相切,∴∠OAP=∠OBP=90°.又∵∠P=50°,
∴∠AOB=360°-90°-90°-50°=130°.
在Rt△AOC和Rt△EOC中,∴Rt△AOC≌Rt△EOC(HL).
∴∠AOC=∠COE.
同理:∠DOE=∠BOD,∴∠DOC=∠AOB=65°.
20、(8分)如图内接于,,CD是的直径,点P是CD延长线上一点,且.
求证:PA是的切线;
若,求的直径.
【答案】(1)详见解析;(2)的直径为.
【分析】
连接OA,根据圆周角定理求出,再根据同圆的半径相等从而可得,继而根据等腰三角形的性质可得出,继而由,可得出,从而得出结论;
利用含的直角三角形的性质求出,可得出,再由,可得出的直径.
连接OA,如图,
,,
又,,
又,,
,
,是的切线.
在中,,,
又,,
,.的直径为.
21、(8分)如图,AB=AC,CD⊥AB于点D,点O是∠BAC的平分线上一点⊙O与AB相切于点M,与CD相切于点N
(1)求证:∠AOC=135°
(2)若NC=3,BC=,求DM的长
【分析】(1)只要证明OC平分∠ACD,即可解决问题;
(2)由切线长定理可知:AM=AE,DM=DN,CN=CE=3,设DM=DN=x,在Rt△BDC中,根据,构建方程即可解决问题.
【详解】(1)证明:连接OM,ON,过O点做OE⊥AC,交AC于E,如图所示,
∵⊙O与AB相切于点M,与CD相切于点N, ∴OM⊥AB,ON⊥CD,
∵OA平分∠BAC,OE⊥AC,OM⊥AB,∴OM=OE,即:E为⊙O的切点;∴OE=ON,
又∵OE⊥AC,ON⊥CD∴OC平分∠ACD
∵CD⊥AB∴∠ADC=90°∴∠DAC+∠ACD=90°∴∠OAC+∠OCA=45°
∴∠AOC=180°-(∠OAC+∠OCA)=180°-45°=135°,即:∠AOC=135°
(2)由(1)得,AM=AE,DM=DN,CN=CE=3,设DM=DN=x,
∵AB=AC∴BD=AB-AD=AC-AE-DM=CE=DM=3-x
∵CD=3+x
在Rt∆BCD中,由勾股定理得:
即:,解得:x=1或x=-1(舍去),即DM=1.
22、(10分)如图,AB、CD是⊙O中两条互相垂直的弦,垂足为点E,且AE=CE,点F是BC的中点,延长FE交AD于点G,已知AE=1,BE=3,OE=.
(1)求证:△AED≌△CEB;
(2)求证:FG⊥AD;
(3)若一条直线l到圆心O的距离d=,试判断直线l是否是圆O的切线,并说明理由.
【分析】(1)由圆周角定理得∠A=∠C,由ASA得出△AED≌△CEB;
(2)由直角三角形斜边上的中线性质得EF=BC=BF,由等腰三角形的性质得∠FEB=∠B,由圆周角定理和对顶角相等证出∠A+∠AEG=90°,进而得出结论;
(3)作OH⊥AB于H,连接OB,由垂径定理得出AH=BH=AB=2,则EH=AH−AE=1,由勾股定理求出OH=1,OB=,由一条直线l到圆心O的距离d==⊙O的半径,即可得出结论.
【详解】(1)证明:由圆周角定理得:∠A=∠C,
在△AED和△CEB中,,∴△AED≌△CEB(ASA);
(2)证明:∵AB⊥CD,∴∠AED=∠CEB=90°,∴∠C+∠B=90°,
∵点F是BC的中点,∴EF=BC=BF,∴∠FEB=∠B,
∵∠A=∠C,∠AEG=∠FEB=∠B,∴∠A+∠AEG=∠C+∠B=90°,
∴∠AGE=90°,∴FG⊥AD;
(3)解:直线l是圆O的切线,理由如下:作OH⊥AB于H,连接OB,如图所示:
∵AE=1,BE=3,∴AB=AE+BE=4,
∵OH⊥AB,∴AH=BH=AB=2,∴EH=AH﹣AE=1,
∴OH===1,∴OB===,
即⊙O的半径为,
∵一条直线l到圆心O的距离d==⊙O的半径,∴直线l是圆O的切线.
23、(10分)如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE
(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
【答案】(1)证明见解析;(2)阴影部分的面积为.
【分析】(1)连接OC,先证明∠OAC=∠OCA,进而得到OC∥AE,于是得到OC⊥CD,进而证明DE是⊙O的切线;(2)分别求出△OCD的面积和扇形OBC的面积,利用S阴影=S△COD﹣S扇形OBC即可得到答案.
解:(1)连接OC, ∵OA=OC, ∴∠OAC=∠OCA,
∵AC平分∠BAE, ∴∠OAC=∠CAE,
∴∠OCA=∠CAE, ∴OC∥AE, ∴∠OCD=∠E,
∵AE⊥DE, ∴∠E=90°, ∴∠OCD=90°, ∴OC⊥CD,
∵点C在圆O上,OC为圆O的半径, ∴CD是圆O的切线;
(2)在Rt△AED中, ∵∠D=30°,AE=6, ∴AD=2AE=12,
在Rt△OCD中,∵∠D=30°,∴DO=2OC=DB+OB=DB+OC,
∴DB=OB=OC=AD=4,DO=8,∴CD=
∴S△OCD==8, ∵∠D=30°,∠OCD=90°,
∴∠DOC=60°, ∴S扇形OBC=×π×OC2=,
∵S阴影=S△COD﹣S扇形OBC ∴S阴影=8﹣,
∴阴影部分的面积为8﹣.
24、(8分)如图,已知是⊙O的直径,点C、D在⊙O上,点E在⊙O外,.
(1)求证:是⊙O的切线;
(2)当时,求阴影部分的面积.
【答案】(1)见详解;(2)阴影部分的面积为.
【分析】(1)根据AB是⊙O的直径,利用直径所对的圆周角是直角得到∠ACB=90°,结合∠ABC=60°求得∠BAC=30°,从而推出∠BAE=90°,即OA⊥AE,可得AE是⊙O的切线;
(2)连接OC,作OF⊥AC,根据三角形中位线性质得出OF=2,根据圆周角定理得出∠AOC=120°,然后根据S阴影=S扇形-S△AOC即可求得.
【解析】(1)∵∠ABC与∠D都是劣弧AC所对的圆周角,∠D=60°,
∴∠ABC=∠D=60°;
∵AB是⊙O的直径,
∴∠ACB=90°.
可得∠BAC=90°∠ABC=30°,
∴∠BAE=∠BAC+∠EAC=30°+60°=90°,
即BA⊥AE,得OA⊥AE,
又∵OA是⊙O的半径,
∴AE是⊙O的切线;
(2)连接OC,作OF⊥AC,
∴OF垂直平分AC,
∵OA=OB,,
∴OF=BC=2,
∵∠D=60°,
∴∠AOC=120°,∠ABC=60°,
∴AC=,
∴S阴影=S扇形-S△AOC=.
25、(12分)如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作(以下结果保留根号):
(1)利用网格确定该圆弧所在圆的圆心D点的位置,并写出D点的坐标为 ;
(2)连接AD、CD,⊙D的半径为 ,∠ADC的度数为 ;
(3)若扇形DAC是一个圆锥的侧面展开图,求该圆锥底面半径.
【答案】(1)圆心D点的位置见解析,(2,0);(2)2, 90°;(3).
【分析】(1)利用垂径定理可作AB和BC的垂直平分线,两线的交点即为D点,可得出D点坐标;
(2)在△AOD中AO和OD可由坐标得出,利用勾股定理可求得AD和CD,过C作CE⊥x轴于点E,则可证得△OAD≌△EDC,可得∠ADO=∠DCE,可得∠ADO+∠CDE=90°,可得到∠ADC的度数;
(3)先求得扇形DAC的面积,设圆锥底面半径为r,利用圆锥侧面展开图的面积=πr•AD,可求得r.
【解析】(1)如图1,分别作AB、BC的垂直平分线,两线交于点D,
∴D点的坐标为(2,0),
故答案为:(2,0);
(2)如图2,连接AD、CD,过点C作CE⊥x轴于点E,
则OA=4,OD=2,在Rt△AOD中,可求得AD=,
即⊙D的半径为,
且CE=2,DE=4,
∴AO=DE,OD=CE,
在△AOD和△DEC中,
,
∴△AOD≌△DEC(SAS),
∴∠OAD=∠CDE,
∴∠CDE+∠ADO=90°,
∴∠ADC=90°,
故答案为;90°;
(3)弧AC的长=×=π,
设圆锥底面半径为r则有2πr=π,解得:r=,
所以圆锥底面半径为.
26、(12分)如图,在△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A,B,D三点.
(1)求证:AB是⊙O的直径;
(2)判断DE与⊙O的位置关系,并加以证明;
(3)若⊙O的半径为3,∠BAC=60°,求DE的长.
【答案】(1)证明见解析;(2)DE与⊙O相切;(3)
【分析】(1)连接AD,根据等腰三角形三线合一性质得到AD⊥BC,再根据90°的圆周角所对的弦为直径即可证得AB是⊙O的直径;(2)DE与圆O相切,理由为:连接OD,利用中位线定理得到OD∥AC,利用两直线平行内错角相等得到∠ODE为直角,再由OD为半径,即可得证;(3)由AB=AC,且∠BAC=60°,得到DABC为等边三角形,连接BF,DE为DCBF中位线,求出BF的长,即可确定出DE的长.
【解析】解:(1)证明:连接AD,∵AB=AC,BD=DC,∴AD⊥BC,∴∠ADB=90°,∴AB为⊙O的直径;
(2)DE与⊙O相切,理由为:连接OD,
∵O、D分别为AB、BC的中点,∴OD为△ABC的中位线,∴OD∥BC,
∵DE⊥BC,∴DE⊥OD,∵OD为⊙O的半径,∴DE与⊙O相切;
(3)解:连接BF,∵AB=AC,∠BAC=60°,∴△ABC为等边三角形,∴AB=AC=BC=6,
∵AB为⊙O的直径,∴∠AFB=∠DEC=90°,∴AF=CF=3,DE∥BF,
∵D为BC中点,∴E为CF中点,DE=BF,在Rt△ABF中,∠AFB=90°,AB=6,AF=3,
∴BF=,则DE=BF=.
27、(14分)中,,,,点是 的中点,点是直线上方平面内一点(不与、重合),且,以为圆心,为半径作.
(1)如图1,当经过点时,
①为______ 三角形; ②求证:一定经过点; ③阴影部分的面积为______;
(2)如图2,过点作直线于点,且与直线相切,求的长;
(3)设与的另一个交点为,当时,直接写出的长.
【答案】(1)①等边;②见解析;③;(2);(3)或
【分析】(1)①根据经过点,则有,又,即得出结论;②连接、,已得到为等边三角形,进而得出为等边三角形,即可得出结论;③由②可得阴影部分的面积 ,即可得出答案;
(2)设切点为,连接,作于点,可得四边形 是矩形,设,则,在和中,利用勾股定理,列出方程,即可得出答案;(3)过点P作,垂足为点G,则AG=QG,根据点Q的位置可分为两种情况进行讨论即可.
【详解】解:(1)①等边三角形 ∵经过点,∴PA,PD为的半径,即,
∵,∴,∴是等边三角形;
②如图,连接、
为边上中线,
又为等边三角形
又为等边三角形
,为等边三角形
又为半径为半径即一定经过点;
③由②可知
阴影部分的面积 ,
在中,,,,
∴ ,
∴ ,
(2)如图,设切点为,连接,作于点.
与直线相切
,四边形 是矩形,
设,则 中,
中,
解得或(舍去)即相切于时,
(3)如图,过点P作,垂足为点G,则AG=QG,
当点Q在A,D之间时,∵,AD=2,∴AG=QG= ,
在 和 中, ,,
即,解得: 或(舍去);
当点Q在B,D之间时,有, , ,
∴,解得:或(舍去);
综上所述:的长或.
初中2.1 圆精品课后复习题: 这是一份初中2.1 圆精品课后复习题,共33页。试卷主要包含了下列说法正确的是,如图,点A的坐标是等内容,欢迎下载使用。
初中苏科版2.1 圆精品综合训练题: 这是一份初中苏科版2.1 圆精品综合训练题,共23页。试卷主要包含了如图,已知点A等内容,欢迎下载使用。
专题2.13 第2章 对称图形—圆单元测试(培优提升卷)-2021-2022学年九年级数学上册同步培优题典【苏科版】: 这是一份专题2.13 第2章 对称图形—圆单元测试(培优提升卷)-2021-2022学年九年级数学上册同步培优题典【苏科版】,文件包含专题213对称图形圆单元测试培优提升卷-2021-2022学年九年级数学上册尖子生同步培优题典解析版苏科版docx、专题213对称图形圆单元测试培优提升卷-2021-2022学年九年级数学上册尖子生同步培优题典原卷版苏科版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。













