

还剩12页未读,
继续阅读
第02章 小结与思考-2023-2024学年九年级数学上册教材配套教学课件(苏科版)
展开
这是一份第02章 小结与思考-2023-2024学年九年级数学上册教材配套教学课件(苏科版),共20页。
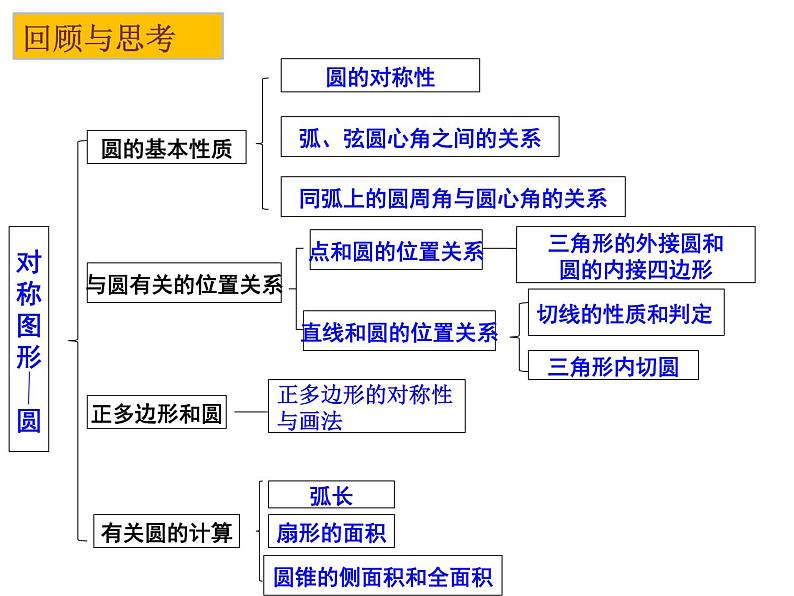
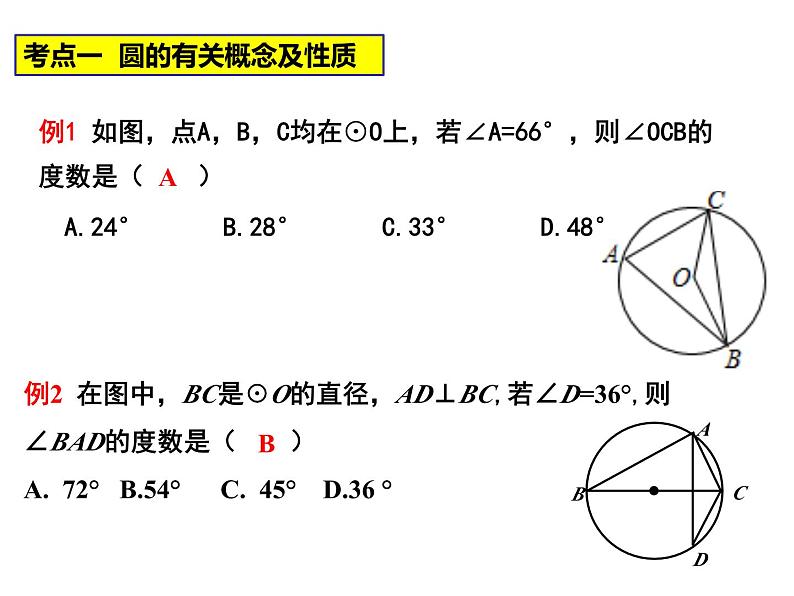
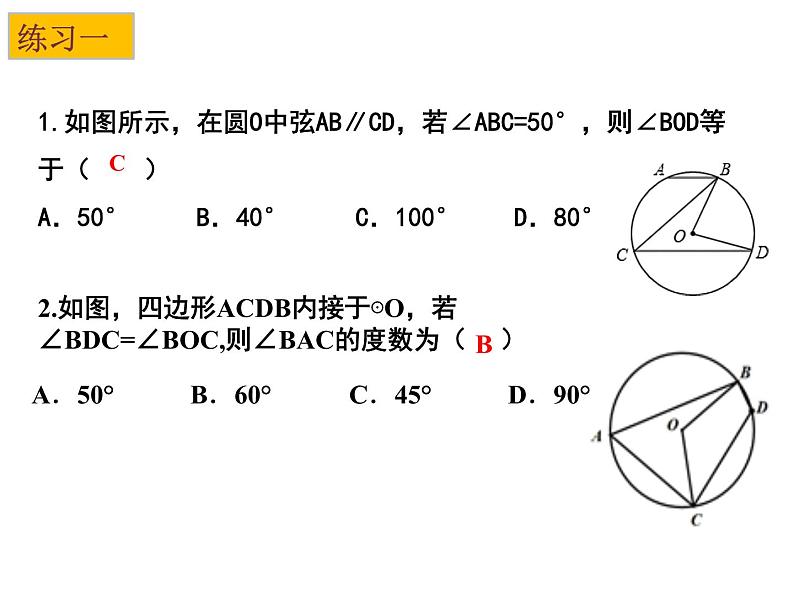
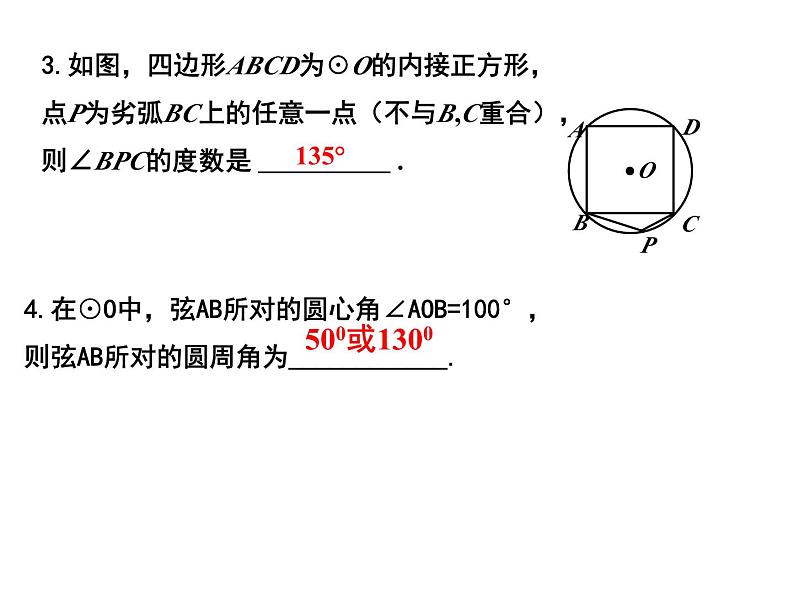
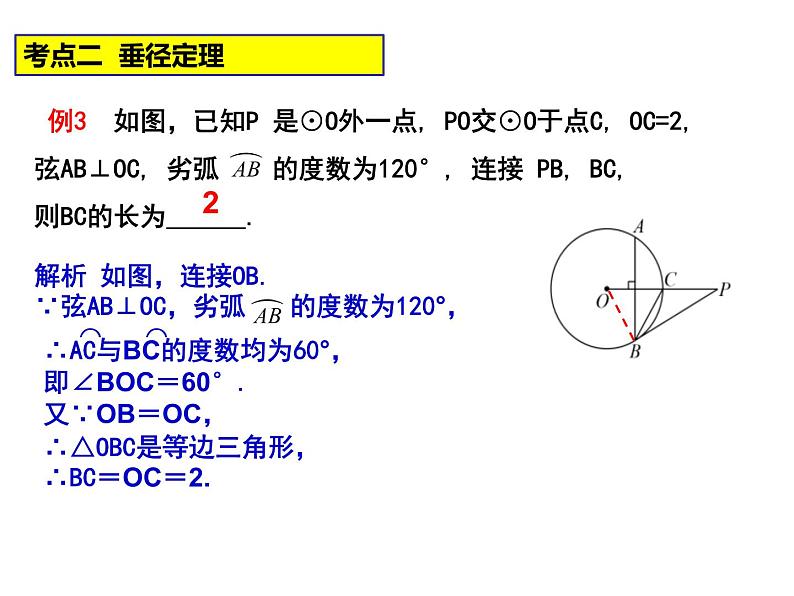
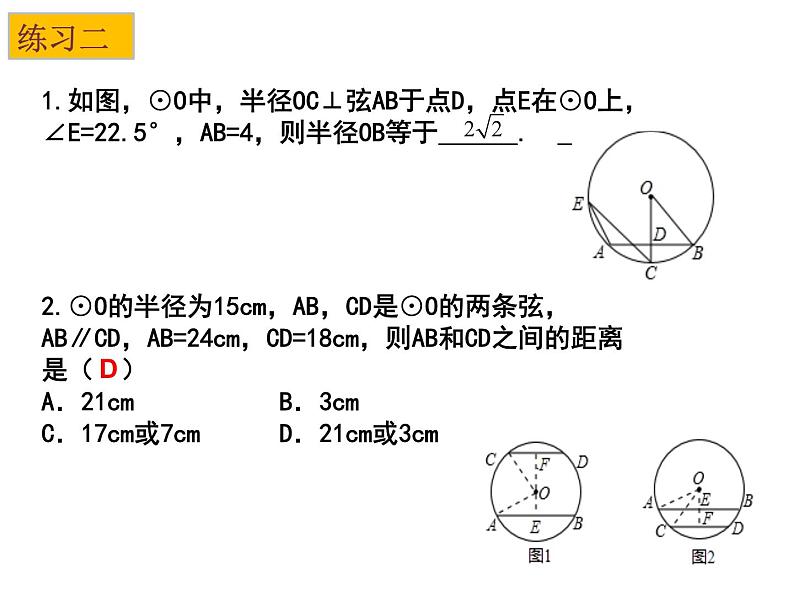
第二章 《对称图形-圆》小结与思考回顾与思考对称图形圆三角形的外接圆和圆的内接四边形正多边形的对称性与画法弧长扇形的面积圆锥的侧面积和全面积考点一 圆的有关概念及性质例1 如图,点A,B,C均在⊙O上,若∠A=66°,则∠OCB的度数是( )AA.24° B.28° C.33° D.48°例2 在图中,BC是☉O的直径,AD⊥BC,若∠D=36°,则∠BAD的度数是( )A. 72° B.54° C. 45° D.36 °B1.如图所示,在圆O中弦AB∥CD,若∠ABC=50°,则∠BOD等于( )A.50° B.40° C.100° D.80°C练习一2.如图,四边形ACDB内接于⊙O,若∠BDC=∠BOC,则∠BAC的度数为( )A.50° B.60° C.45° D.90°B135°3.如图,四边形ABCD为☉O的内接正方形,点P为劣弧BC上的任意一点(不与B,C重合),则∠BPC的度数是 .4.在⊙O中,弦AB所对的圆心角∠AOB=100°,则弦AB所对的圆周角为____________.500或1300 考点二 垂径定理 21.如图,⊙O中,半径OC⊥弦AB于点D,点E在⊙O上,∠E=22.5°,AB=4,则半径OB等于 . 2.⊙O的半径为15cm,AB,CD是⊙O的两条弦,AB∥CD,AB=24cm,CD=18cm,则AB和CD之间的距离是( )A.21cm B.3cmC.17cm或7cm D.21cm或3cmD练习二例4 ☉O的半径为R,圆心到点A的距离为d,且R、d分别是方程x2-6x+8=0的两根,则点A与☉O的位置关系是( )A.点A在☉O内部 B.点A在☉O上C.点A在☉O外部 D.点A不在☉O上解:此题需先计算出一元二次方程x2-6x+8=0的两个根,然后再根据R与d的之间的关系判断出点A与 ☉O的关系.D考点三 与圆有关的位置关系 例5 如图,在Rt△ABC中,∠ABC=90°,以AB为直径的☉O交AC于点D,连接BD,取BC的中点E,连接ED。求证:ED与☉O相切.例6 如图,在Rt△ABC中,∠ABC=90°,以AB为直径的☉O交AC于点D,过点D的切线交BC于E.求证:BC=2DE.练习三1.如图,线段AB是直径,点D是☉O上一点, ∠CDB=20 °,过点C作☉O的切线交AB的延长线于点E,则∠E等于 .5002.如图,AE,AD,BC分别切⊙O于点E、D和点F,若AD=8cm,则△ABC的周长为_______cm.163.如图, O为正方形对角线上一点,以点O 为圆心,OA长为半径的☉O与BC相切于点M. (1)求证:CD与☉O相切;(1)证明:过点O作ON⊥CD于N.连接OM ∵BC与☉O相切于点M, ∴ ∠OMC=90 °, ∵四边形ABCD是正方形,点O在AC上.∴AC是∠BCD的角平分线,∴ON=OM,∴ CD与☉O相切.N(2)若正方形ABCD的边长为1,求☉O的半径.(1)证切线时添加辅助线的解题方法有两种: ①有公共点,连半径,证垂直; ②无公共点,作垂直,证半径;有切线时添加辅助线的解题方法是:见切点,连半径,得垂直;(2)设未知数,通常利用勾股定理建立方程.例7 如图,四边形OABC为菱形,点B、C在以点O为圆心的圆上, OA=1,∠AOC=120°,∠1=∠2,则扇形OEF的面积?考点四 与圆有关的计算 1.一条弧所对的圆心角为135 ° ,弧长等于半径为5cm的圆的周长的3倍,则这条弧的半径为 . 2.若一个正六边形的周长为24,则该正六边形的面积为_____.40cm练习四3.如图,已知C,D是以AB为直径的半圆周上的两点,O是圆心,半径OA=2,∠COD=120°,则图中阴影部分的面积等于______.4. 如图,正六边形ABCDEF内接于半径为5的⊙O,四边形EFGH是正方形.⑴求正方形EFGH的面积;解:⑴∵正六边形的边长与其半径相等, ∴EF=OF=5. ∵四边形EFGH是正方形, ∴FG=EF=5, ∴正方形EFGH的面积是25.⑵∵正六边形的边长与其半径相等,∴∠OFE=60°.∴正方形的内角是90°,∴∠OFG=∠OFE +∠EFG=60°+90°=150°.由⑴得OF=FG,∴∠OGF= (180°-∠OFG) =(180°-150°)=15°.⑵连接OF、OG,求∠OGF的度数.例8 如何解决“破镜重圆”的问题:·考点五 与圆有关的作图 如何作圆内接正五边形怎么作?(1)用量角器作72°的中心角,得圆的五等分点;(2)依次连接各等分点,得圆的内接正五边形.课堂小结你还有哪些困惑与疑问?你能完整地回顾本章所学的有关圆的知识吗?你学会了哪些与圆有关的证明方法?通过本节课的学习,你有哪些收获?
第二章 《对称图形-圆》小结与思考回顾与思考对称图形圆三角形的外接圆和圆的内接四边形正多边形的对称性与画法弧长扇形的面积圆锥的侧面积和全面积考点一 圆的有关概念及性质例1 如图,点A,B,C均在⊙O上,若∠A=66°,则∠OCB的度数是( )AA.24° B.28° C.33° D.48°例2 在图中,BC是☉O的直径,AD⊥BC,若∠D=36°,则∠BAD的度数是( )A. 72° B.54° C. 45° D.36 °B1.如图所示,在圆O中弦AB∥CD,若∠ABC=50°,则∠BOD等于( )A.50° B.40° C.100° D.80°C练习一2.如图,四边形ACDB内接于⊙O,若∠BDC=∠BOC,则∠BAC的度数为( )A.50° B.60° C.45° D.90°B135°3.如图,四边形ABCD为☉O的内接正方形,点P为劣弧BC上的任意一点(不与B,C重合),则∠BPC的度数是 .4.在⊙O中,弦AB所对的圆心角∠AOB=100°,则弦AB所对的圆周角为____________.500或1300 考点二 垂径定理 21.如图,⊙O中,半径OC⊥弦AB于点D,点E在⊙O上,∠E=22.5°,AB=4,则半径OB等于 . 2.⊙O的半径为15cm,AB,CD是⊙O的两条弦,AB∥CD,AB=24cm,CD=18cm,则AB和CD之间的距离是( )A.21cm B.3cmC.17cm或7cm D.21cm或3cmD练习二例4 ☉O的半径为R,圆心到点A的距离为d,且R、d分别是方程x2-6x+8=0的两根,则点A与☉O的位置关系是( )A.点A在☉O内部 B.点A在☉O上C.点A在☉O外部 D.点A不在☉O上解:此题需先计算出一元二次方程x2-6x+8=0的两个根,然后再根据R与d的之间的关系判断出点A与 ☉O的关系.D考点三 与圆有关的位置关系 例5 如图,在Rt△ABC中,∠ABC=90°,以AB为直径的☉O交AC于点D,连接BD,取BC的中点E,连接ED。求证:ED与☉O相切.例6 如图,在Rt△ABC中,∠ABC=90°,以AB为直径的☉O交AC于点D,过点D的切线交BC于E.求证:BC=2DE.练习三1.如图,线段AB是直径,点D是☉O上一点, ∠CDB=20 °,过点C作☉O的切线交AB的延长线于点E,则∠E等于 .5002.如图,AE,AD,BC分别切⊙O于点E、D和点F,若AD=8cm,则△ABC的周长为_______cm.163.如图, O为正方形对角线上一点,以点O 为圆心,OA长为半径的☉O与BC相切于点M. (1)求证:CD与☉O相切;(1)证明:过点O作ON⊥CD于N.连接OM ∵BC与☉O相切于点M, ∴ ∠OMC=90 °, ∵四边形ABCD是正方形,点O在AC上.∴AC是∠BCD的角平分线,∴ON=OM,∴ CD与☉O相切.N(2)若正方形ABCD的边长为1,求☉O的半径.(1)证切线时添加辅助线的解题方法有两种: ①有公共点,连半径,证垂直; ②无公共点,作垂直,证半径;有切线时添加辅助线的解题方法是:见切点,连半径,得垂直;(2)设未知数,通常利用勾股定理建立方程.例7 如图,四边形OABC为菱形,点B、C在以点O为圆心的圆上, OA=1,∠AOC=120°,∠1=∠2,则扇形OEF的面积?考点四 与圆有关的计算 1.一条弧所对的圆心角为135 ° ,弧长等于半径为5cm的圆的周长的3倍,则这条弧的半径为 . 2.若一个正六边形的周长为24,则该正六边形的面积为_____.40cm练习四3.如图,已知C,D是以AB为直径的半圆周上的两点,O是圆心,半径OA=2,∠COD=120°,则图中阴影部分的面积等于______.4. 如图,正六边形ABCDEF内接于半径为5的⊙O,四边形EFGH是正方形.⑴求正方形EFGH的面积;解:⑴∵正六边形的边长与其半径相等, ∴EF=OF=5. ∵四边形EFGH是正方形, ∴FG=EF=5, ∴正方形EFGH的面积是25.⑵∵正六边形的边长与其半径相等,∴∠OFE=60°.∴正方形的内角是90°,∴∠OFG=∠OFE +∠EFG=60°+90°=150°.由⑴得OF=FG,∴∠OGF= (180°-∠OFG) =(180°-150°)=15°.⑵连接OF、OG,求∠OGF的度数.例8 如何解决“破镜重圆”的问题:·考点五 与圆有关的作图 如何作圆内接正五边形怎么作?(1)用量角器作72°的中心角,得圆的五等分点;(2)依次连接各等分点,得圆的内接正五边形.课堂小结你还有哪些困惑与疑问?你能完整地回顾本章所学的有关圆的知识吗?你学会了哪些与圆有关的证明方法?通过本节课的学习,你有哪些收获?
相关资料
更多










