





新教材2022届高考数学人教版一轮复习课件:7.4.1 余弦定理、正弦定理及应用举例
展开【教材回扣】1.正弦定理、余弦定理在△ABC中,若角A、B、C所对的边分别是a,b,c,R为△ABC外接圆半径,则
b2+c2-2bccsA
a2+c2-2accsB
a2+b2-2abcsC
sinA∶sinB∶sinC
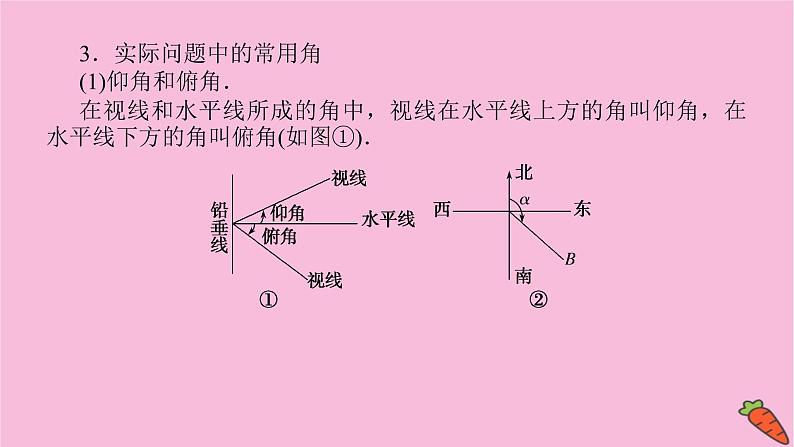
3.实际问题中的常用角(1)仰角和俯角.在视线和水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下方的角叫俯角(如图①).
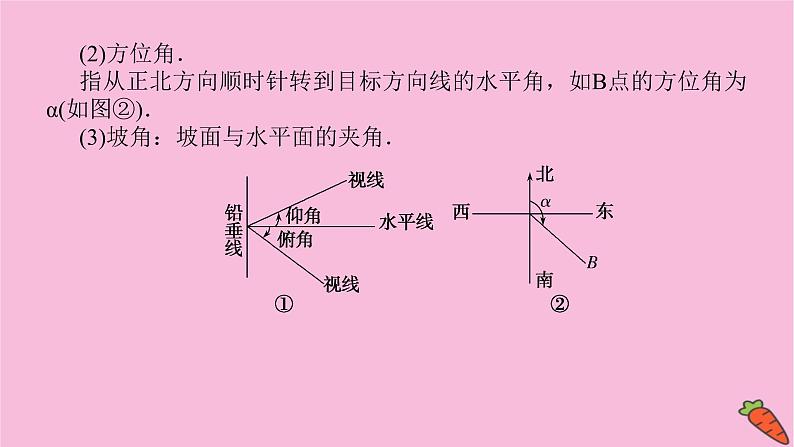
(2)方位角.指从正北方向顺时针转到目标方向线的水平角,如B点的方位角为α(如图②).(3)坡角:坡面与水平面的夹角.
【题组练透】题组一 判断正误(正确的打“√”,错误的打“×”)1.三角形中三边之比等于相应的三个内角之比.( )2.当b2+c2-a2>0时,△ABC为锐角三角形.( )3.从A处望B处的仰角为α,从B处望A处的俯角为β,则α,β的关系为α+β=180°.( )4.方位角与方向角其实质是一样的,均是确定观察点与目标点之间的位置关系.( )
2.在△ABC中,若sin 2A=sin 2C,则△ABC的形状是( )A.等边三角形B.等腰三角形C.直角三角形D.等腰三角形或直角三角形
3.设△ABC的内角A,B,C所对边的长分别为a,b,c.若b+c=2a,3sin A=5sin B,则C=________.
类题通法(1)正弦定理、余弦定理的作用是在已知三角形部分元素的情况下求解其余元素,基本思想是方程思想,即根据正弦定理、余弦定理列出关于未知元素的方程,通过解方程求得未知元素.(2)正弦定理、余弦定理的另一个作用是实现三角形边角关系的互化,解题时可以把已知条件化为角的三角函数关系,也可以把已知条件化为三角形边的关系.(3)在三角形的判断中注意应用“大边对大角”来确定.
[例2] [2020·全国卷Ⅱ]△ABC中,sin2A-sin2B-sin2C=sin B sin C.(1)求A;(2)若BC=3,求△ABC周长的最大值.
类题通法(1)正弦定理和余弦定理并不是孤立的,解题时要根据具体题目合理运用,有时还需要交替使用.(2)条件中出现平方关系多考虑余弦定理,出现一次式,一般要考虑正弦定理.
题型二 正弦定理、余弦定理的综合应用角度1|判断三角形的形状[例3] (1)[2021·山东省实验中学第一次诊断性考试]在△ABC中,角A,B,C所对的边分别为a,b,c,若a sin A+b sin B
类题通法判断三角形形状的两种思路 (1)化边:通过因式分解、配方等得出边的相应关系,从而判断三角形的形状.(2)化角:通过三角恒等变换,得出内角的关系,从而判断三角形的形状.此时要注意应用A+B+C=π这个结论.
类题通法求三角形面积的方法(1)若三角形中已知一个角(角的大小或该角的正、余弦值),结合题意求解这个角的两边或该角的两边之积,代入公式求面积.(2)若已知三角形的三边,可先求其一个角的余弦值,再求其正弦值,代入公式求面积,总之,结合图形恰当选择面积公式是解题的关键.
(2)△ABC的内角A,B,C的对边分别为a,b,c.已知b sin C+c sin B=4a sin B sin C,b2+c2-a2=8,则△ABC的面积为________.
类题通法 (1)根据已知的边角画出图形并在图中标示; (2)选择在某个三角形中运用正弦定理或余弦定理.
题型三 正弦定理、余弦定理的应用举例[例6] (1)济南泉城广场上的泉标是隶书“泉”字,其造型流畅别致,成了济南的标志和象征.李明同学想测量泉标的高度,于是他在广场的A点测得泉标顶端的仰角为60°,他又沿着泉标底部方向前进15.2 m,到达B点,又测得泉标顶端的仰角为80°.则李明同学求出泉标的高度为________m.(精确到1 m)(参考数据:sin 20°≈0.342,sin 80°≈0.985)
(2)在一次抗洪抢险中,某救生艇发动机突然发生故障停止转动,失去动力的救生艇在洪水中漂行,此时,风向是北偏东30°,风速是20 km/h;水的流向是正东,流速是20 km/h,若不考虑其他因素,救生艇在洪水中漂行的速度的方向为北偏东________,大小为________km/h.
类题通法正、余弦定理应用举例的类型及解题策略1.求距离、高度问题(1)选定或确定要创建的三角形,要先确定所求量所在的三角形,若其他量已知则直接解;若有未知量,则把未知量放在另一确定三角形中求解.有时需设出未知量,从几个三角形中列出方程(组),解方程(组)得出所要求的量.(2)确定用正弦定理还是余弦定理,如果都可用,就选择更便于计算的定理.
2.求角度问题(1)分析题意,分清已知与所求,再根据题意画出正确的示意图,这是最关键、最重要的一步,画图时,要明确仰角、俯角、方位角以及方向角的含义,并能准确找到这些角.(2)将实际问题转化为可用数学方法解决的问题后,注意正、余弦定理的综合应用.
巩固训练6:海洋蓝洞是地球罕见的自然地理现象,被喻为“地球留给人类保留宇宙秘密的最后遗产”,我国拥有世界上最深的海洋蓝洞,若要测量如图所示的蓝洞的口径A,B两点间的距离,现在珊瑚群岛上取两点C,D,测得CD=80,∠ADB=135°,∠BDC=∠DCA=15°,∠ACB=120°,求A,B两点的距离.
状 元 笔 记 射影定理的活用设△ABC的三边是a,b,c,它们所对的角分别是A,B,C,则有:a=b cs C+c cs B;b=c cs A+a cs C;c=a cs B+b cs A.注:以“a=b cs C+c cs B”为例,b,c在a上的射影分别为b cs C,c cs B,故名射影定理.
证明 如图,在△ABC中,AD⊥BC,则b cs C=CD,c cs B=BD,故b cs C+c cs B=CD+BD=BC=a,即a=b cs C+c cs B,同理可证b=c cs A+a cs C,c=a cs B+b cs A.
[典例1] [2017·山东卷]在△ABC中,角A,B,C的对边分别为a,b,c.若△ABC为锐角三角形,且满足sin B(1+2cs C)=2sin A cs C+cs A sin C,则下列等式成立的是( )A.a=2b B.b=2a C.A=2B D.B=2A
【应用示范】 由正弦定理及sin B(1+2cs C)=2sin A cs C+cs A sin C得b+2b cs C=2a cs C+c cs A=a cs C+(a cs C+c cs A)=a cs C+b,即2b cs C=a cs C,又因为△ABC为锐角三角形,所以cs C≠0,则2b=a.
[典例2] [2017·全国卷Ⅱ]△ABC的内角A,B,C的对边分别为a,b,c,若2b cs B=a cs C+c cs A,则B=____.
【探究】 射影定理和正、余弦定理一样实现了边角之间的转换,运用射影定理整体代入,大大简化了运算过程,取得了事半功倍的神奇效果.
高中数学人教A版 (2019)必修 第二册6.4 平面向量的应用教课内容ppt课件: 这是一份高中数学人教A版 (2019)必修 第二册6.4 平面向量的应用教课内容ppt课件,共19页。PPT课件主要包含了余弦定理,余弦定理推论,正弦定理,正弦定理的变形,用余弦定理求解,用正弦定理求解,仰角和俯角,方向角,方位角,测量距离等内容,欢迎下载使用。
人教A版 (2019)必修 第二册第六章 平面向量及其应用6.4 平面向量的应用集体备课课件ppt: 这是一份人教A版 (2019)必修 第二册第六章 平面向量及其应用6.4 平面向量的应用集体备课课件ppt,共20页。PPT课件主要包含了教学目标,复习回顾,余弦定理,正弦定理,探究新知,经纬仪,方向角,方位角,应用举例,由正弦定理得等内容,欢迎下载使用。
数学必修 第二册第六章 平面向量及其应用6.4 平面向量的应用完美版课件ppt: 这是一份数学必修 第二册第六章 平面向量及其应用6.4 平面向量的应用完美版课件ppt,文件包含644《正弦定理余弦定理应用举例》课件pptx、644《正弦定理余弦定理应用举例》教案docx等2份课件配套教学资源,其中PPT共38页, 欢迎下载使用。












