

人教版九年级下册27.2 相似三角形综合与测试练习
展开
27.2相似三角形同步练习人教版初中数学九年级下册
一、选择题(本大题共12小题,共36.0分)
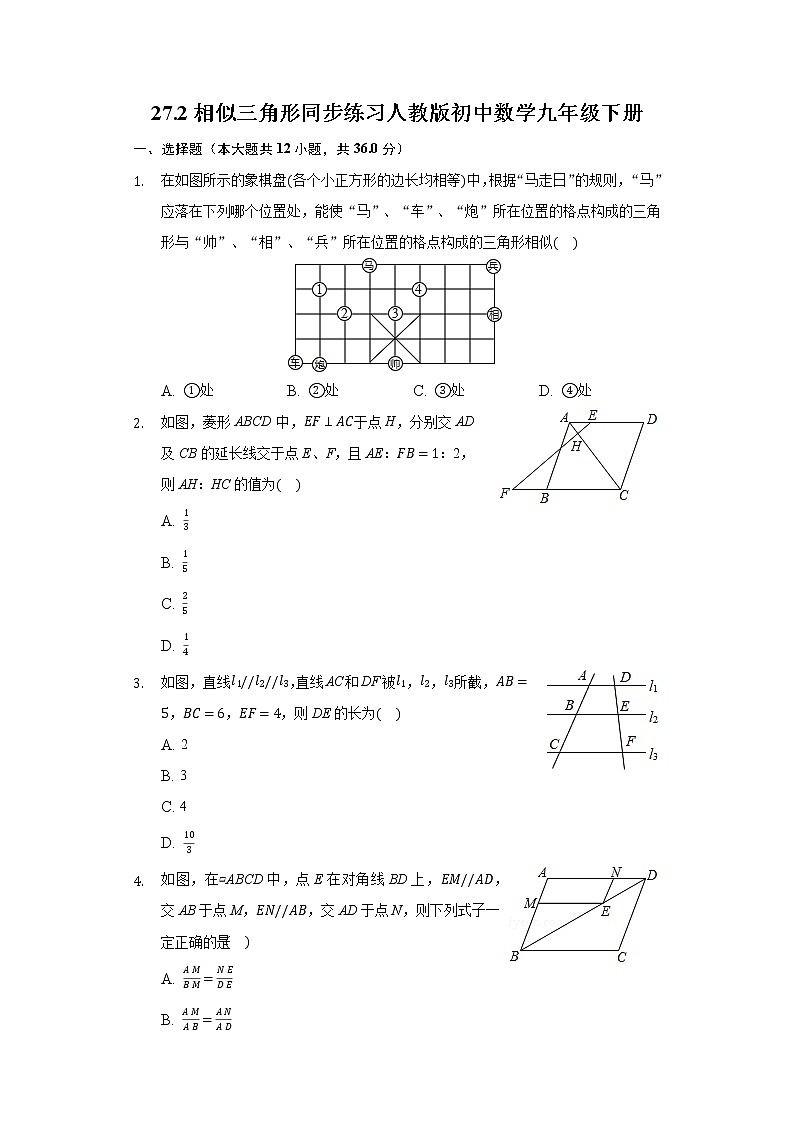
- 在如图所示的象棋盘各个小正方形的边长均相等中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”、“兵”所在位置的格点构成的三角形相似
A. 处 B. 处 C. 处 D. 处
- 如图,菱形ABCD中,于点H,分别交AD及CB的延长线交于点E、F,且AE::2,则AH:HC的值为
A.
B.
C.
D.
- 如图,直线,直线AC和DF被,,所截,,,,则DE的长为
A. 2
B. 3
C. 4
D.
- 如图,在▱ABCD中,点E在对角线BD上,,交AB于点M,,交AD于点N,则下列式子一定正确的是
A.
B.
C.
D.
- 已知∽,且相似比为1:2,则与的面积比为
A. 1:4 B. 4:1 C. 1:2 D. 2:1
- 如图,下列四个选项不一定成立的是
A. ∽
B. ∽
C. ∽
D. ∽
- 为了加强视力保护意识,小明要在书房里挂一张视力表.由于书房空间狭小,他想根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表.如图,如果大视力表中“E”的高度是,那么小视力表中相应“E”的高度是
A. 3cm B. C. D.
- 小明的身高为米,某一时刻他在阳光下的影长为2米,与他邻近的一棵树的影长为6米,则这棵树的高为
A. 米 B. 米 C. 米 D. 米
- 如图,为了测量一池塘的宽DE,在岸边找到一点C,测得,在DC的延长线上找一点A,测得,过点A作交EC的延长线于B,测出,则池塘的宽DE为
A. 32m B. 36m C. 48m D. 56m
- 如图,在中,,的平分线BF交AC于点F,点D、点E分别是边AB、AC上的点,若,则的值为
A. 3
B.
C. 4
D.
- 如图,平行于BC的直线DE把分成面积相等的两部分,则的值为
A. 1 B. C. D.
- 如图,在平行四边形ABCD中,E是DC上的点,,连接AE交BD于点F,则与的面积之比为
A.
B.
C.
D.
二、填空题(本大题共4小题,共12.0分)
- 如图,在正方形网格中,每个小正方形的边长均为1,和的顶点都在网格线的交点上.设的周长为,的周长为,则的值等于______.
|
- 九章算术中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D观察井水水岸C,视线DC与井口的直径AB交于点E,如果测得米,米,米,那么井深AC为______米.
|
- 如果两个相似三角形的相似比为2:3,两个三角形的周长的和是100cm,那么较小的三角形的周长为______cm.
- 如图,BD是的直径,A是外一点,点C在上,AC与相切于点C,,若,,,则弦BC的长为______.
|
三、计算题(本大题共4小题,共24.0分)
- 如图是夹文件用的铁塑料夹子在常态下的侧面示意图.AC,BC表示铁夹的两个面,O点是轴,于已知,,已知文件夹是轴对称图形,试利用图,求图中A,B两点的距离:.
- 如图,点D、E分别在AC、BC上,如果测得,,,,,求A、B两地间的距离.
|
- 如图,在中,点D在AB边上,,
求证:∽;
若,求AC的长.
- 如图,在中,D、E、F分别是AB、BC上的点,且,,,,求EF和FC的长.
|
四、解答题(本大题共2小题,共16.0分)
- 如图,一块材料的形状是锐角三角形ABC,边,高,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
|
- 如图,在锐角中,点D、E分别在边AB、AC上,于点M,于点N,
求证:∽;
若,,求的值.
答案和解析
1.【答案】B
【解析】
【分析】
本题考查了相似三角形的知识,解题的关键是利用勾股定理求得三角形的各边的长,难度不大.
确定“帅”、“相”、“兵”所在位置的格点构成的三角形的三边的长,然后利用相似三角形的对应边的比相等确定第三个顶点的位置即可.
【解答】
解:帅”、“相”、“兵”所在位置的格点构成的三角形的三边的长分别为2、、;
“车”、“炮”之间的距离为1,
“炮”之间的距离为,“车”之间的距离为,
,
马应该落在的位置,
故选:B.
2.【答案】B
【解析】解:设EF与AB交于点G,
四边形ABCD是菱形,
,
,
,
是等腰三角形,
,
,
∽,
,
,
,
,
,
∽,
,
故选:B.
本题考查相似三角形,解题的关键是熟练运用相似三角形的对应边成比例来解答,本题属于中等题型.
易证是等腰三角形,从而可知,再证明∽,∽,利用相似三角形的对应边成比例即可求出答案.
3.【答案】D
【解析】解:直线,
,
,,,
,
,
故选:D.
根据平行线分线段成比例定理得出比例式,代入求出即可.
本题考查了平行线分线段成比例定理,能根据平行线分线段成比例定理得出正确的比例式是解此题的关键.
4.【答案】D
【解析】
【分析】
此题主要考查相似三角形的性质及平行四边形的性质,本题关键是要懂得找相似三角形,利用相似三角形的性质求解.根据平行四边形的性质以及相似三角形的性质.
【解答】
解:在▱ABCD中,,,
四边形AMEN为平行四边形,,,
易得∽∽,
,,A项错误;
,B项错误;
,C项错误;
,D项正确;
故选:D.
5.【答案】A
【解析】
【分析】
此题考查了相似三角形的性质,熟练掌握相似三角形的性质是解本题的关键.利用相似三角形面积之比等于相似比的平方计算即可.
【角度】
解:∽,且相似比为1:2,
与的面积比为1:4,
故选A.
6.【答案】C
【解析】解:,,
∽.
同法可证:∽.
,,
,
,
∽,
故选:C.
利用圆周角定理、园内接四边形的性质一一判断即可;
本题考查相似三角形的判定、圆周角定理、圆内接四边形的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
7.【答案】D
【解析】解:由题意得:,
,
,,,
,
,
故选:D.
直接利用平行线分线段成比例定理列比例式,代入可得结论.
本题考查了相似三角形的应用,比较简单;根据生活常识,墙与地面垂直,则两张视力表平行,根据平行相似或平行线分线段成比例定理列比例式,可以计算出结果.
8.【答案】C
【解析】解:据相同时刻的物高与影长成比例,
设这棵树的高度为xm,
则可列比例为,,
解得,.
故选:C.
在同一时刻物高和影长成正比,即在同一时刻的两个问题物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.
本题主要考查了同一时刻物高和影长成正比,考查利用所学知识解决实际问题的能力.
9.【答案】C
【解析】解:,
∽,
,
,
,
故选:C.
根据相似三角形的性质即可解决问题;
本题考查平行线的性质、相似三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
10.【答案】D
【解析】解:如图,延长DE,BF交于点G,
,,
∽,
,
,
,
的平分线BF交AC于点F,
,
,
,
,
∽,
,
,
,
则.
故选:D.
延长DE,BF交于点G,可证∽,得,得出,可证∽,求出,则的值可求.
本题考查了相似三角形的判定和性质及等腰三角形的判定与性质,正确作出辅助线是解题的关键.
11.【答案】C
【解析】
【分析】本题考查了相似三角形的判定,相似三角形的性质,面积比等于相似比的平方的逆用等.由平行于BC的直线DE把分成面积相等的两部分,可知与相似,且面积比为,则相似比为,从而求出的值.
【解答】
解:,,.
,,.
故选C.
12.【答案】C
【解析】
【分析】此题主要考查平行四边形的性质和相似三角形的判定与性质,根据平行四边形对边平行且相等和已知的,求得两相似三角形对应边的比,再根据相似三角形面积比等于相似比的平方求解.
【解答】
解:因为四边形ABCD为平行四边形,所以,.
所以∽因为,
所以,即.
所以与的面积比为.
故选C.
13.【答案】
【解析】解:,
,
,
,
∽,
,
故答案为:.
先证明两个三角形相似,再根据相似三角形的周长比等于相似比,得出周长比的值便可.
本题主要考查相似三角形的性质与判定,勾股定理,本题关键是证明三角形相似.
14.【答案】7
【解析】解:,,
,
∽,
,
,
,
即井深AC为7米,
故答案为7.
首先证明∽,得到,将相关数值代入,求出AC即可.
本题考查了相似三角形的应用,正确的识别图形是解题的关键.
15.【答案】40
【解析】
【分析】
根据相似三角形周长比等于相似比列式计算.
本题考查的是相似三角形的性质,掌握相似三角形周长比等于相似比是解题的关键.
【解答】
解:设较小的三角形的周长为xcm,则较大的三角形的周长为,
两个相似三角形的相似比为2:3,
两个相似三角形的周长比为2:3,
,
解得,,
故答案为:40.
16.【答案】
【解析】解:连接CD、OC,如图:
与相切于点C,
,
,
,
,
,
,
,
,
是的直径,
,
∽,
,
,
;
故答案为:.
连接CD、OC,由切线的性质得出,证出,由平行线的性质和等腰三角形的性质得出,由圆周角定理得出,证明∽,得出,即可得出结果.
本题考查了切线的性质、圆周角定理、等腰三角形的性质、相似三角形的判定与性质、平行线的性质;熟练掌握切线的性质和圆周角定理,证明三角形相似是解题的关键.
17.【答案】解:如图,连接AB,与CO的延长线交于点E,
夹子是轴对称图形,对称轴是CE,A、B为一组对称点,
,.
在、中,
,是公共角,
∽,
.
又,
,
.
【解析】根据题意,易得∽得,由勾股定理得出OC的值代入比例式即可.
本题利用了相似三角形的性质求解,难易程度适中.
18.【答案】解:,,,,
,.
:::3,CD:::3.
::BC.
,
∽.
:::3.
.
、B两地间的距离为135m.
【解析】此题考查了相似三角形的判定与性质,相似三角形的对应边成比例;
对应边成比例,且对应角相等的三角形相似.要注意方程思想的应用.
本题只要是把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程求出A、B两地间的距离,体现了转化的思想.
19.【答案】解:,,
∽
解:∽
,
,,
,
.
【解析】根据相似三角形的判定即可求出答案.
根据相似三角形的性质即可求出答案.
本题考查相似三角形,解题的关键是熟练运用相似三角形的性质与判定,本题属于基础题型.
20.【答案】解:,
,即,
,
,
,
,即,
,
.
【解析】根据平行线分线段成比例定理,由得,可计算出,则,然后再由得到,可计算出,所以.
本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.
21.【答案】解:四边形EGFH为正方形,
,
∽;
设正方形零件的边长为x mm,则,,
,
∽,
,
,
,
解得:.
答:正方形零件的边长为48mm.
【解析】根据正方形的对边平行得到,利用“平行于三角形的一边的直线截其它两边或其它两边的延长线,得到的三角形与原三角形相似”,设正方形零件的边长为,则,,根据相似三角形的性质得到比例式,解方程即可得到结果.
本题考查了正方形的性质、相似三角形的应用,注意数形结合的运用是解题关键.
22.【答案】证明:,
,
,且
∽
∽
,
∽
【解析】由余角的性质可得,且,可证∽;
由相似三角形的性质可得,通过证明∽,可得.
本题考查了相似三角形的判定和性质,熟练运用相似三角形的判定是本题的关键.
专题07 : 27.2 相似三角形- 期末复习专题训练 2021-2022学年人教版数学九年级下册: 这是一份专题07 : 27.2 相似三角形- 期末复习专题训练 2021-2022学年人教版数学九年级下册,共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
专题05 : 27.2 相似三角形- 期末复习专题训练 2021-2022学年人教版数学九年级下册: 这是一份专题05 : 27.2 相似三角形- 期末复习专题训练 2021-2022学年人教版数学九年级下册,共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
专题06 :27.2 相似三角形- 期末复习专题训练 2021-2022学年人教版数学九年级下册: 这是一份专题06 :27.2 相似三角形- 期末复习专题训练 2021-2022学年人教版数学九年级下册,共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。















