





数学必修 第一册5.1 任意角和弧度制评课ppt课件
展开一、弧度制1.(1)在平面几何中,1°的角是怎样定义的?提示:将圆周分成360等份,每一段圆弧所对的圆心角就是1°的角.(2)在我们度量长度时,有时用“米”作单位,有时用“尺”作单位,有不同的单位制,度量质量时,可以使用“千克”、“磅”等不同的单位制,角的度量除了角度制外,是否也有不同的单位制呢?提示:有不同的单位制,即弧度制.
2.填空弧度制的定义3.将半径为r的圆的一条半径OA,绕圆心顺时针旋转到OB,若弧AB长为2r,则∠AOB的大小为多少弧度?提示:-2弧度.
4.填空弧度数的计算5.做一做已知半径为12 cm,弧长为8π cm的弧,其所对的圆心角为α,则α的弧度数的绝对值是 .
二、角度与弧度的换算1.由360°=2π rad,180°=π rad,你能进行角的角度数与弧度数的转换吗?即1°的角等于多少弧度?1 rad的角等于多少度?
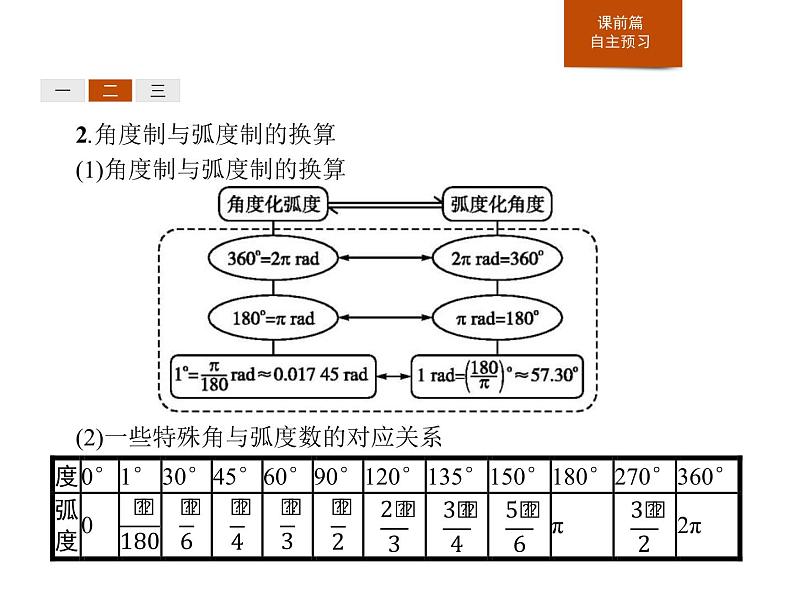
2.角度制与弧度制的换算(1)角度制与弧度制的换算
(2)一些特殊角与弧度数的对应关系
3.做一做下列换算结果错误的是( )
三、弧度制下扇形的弧长与面积公式1.在弧度制下,弧长公式和扇形面积公式可以写成什么形式?你能推导吗?
2.填空扇形的弧长及面积公式设扇形的半径为R,弧长为l,α为其圆心角,则
3.做一做已知扇形的半径r=30,圆心角α= ,则该扇形的弧长等于 ,面积等于 ,周长等于 . 答案:5π 75π 60+5π.
弧度制的概念例1(多选题)下列说法中正确的是( )A.弧度角与实数之间建立了一一对应的关系C.根据弧度的定义,180°一定等于π弧度D.无论是用角度制还是用弧度制度量角,角的大小均与圆的半径的大小有关解析:无论是用角度制还是用弧度制度量角,角的大小均与圆的半径的大小无关,而是与弧长和半径的比值有关,故D项错误.答案:ABC
反思感悟 1.不管是以“弧度”还是以“度”为单位的角的大小都是一个与圆的半径的大小无关的定值.2.用角度制和弧度制度量零角,单位不同,但数量相同(都是0);用角度制和弧度制度量任一非零角,单位不同,数量也不同.3.以弧度为单位表示角的大小时,“弧度”或“rad”通常省略不写,但以度为单位表示角的大小时,“度”或“°”不能省去.4.以弧度为单位度量角时,常把弧度数写成nπ(n∈R)的形式.若无特别要求,不必把π写成小数,如45°= rad,不必写成45°≈0.785 rad.
变式训练1下列说法正确的是( )A.1弧度是长度等于半径的弧B.1弧度是1°的圆心角所对的弧C.1弧度是长度等于半径的圆弧所对的圆心角D.1弧度等于1°解析:1弧度角的定义:长度等于半径的圆弧所对的圆心角叫做1弧度的角.由上可知,只有C正确.答案:C
弧度与角度的换算例2(1)把112°30'化为弧度;(3)将-1 485°表示成2kπ+α(k∈Z)的形式,且0≤α<2π.
反思感悟 角度制与弧度制互化的关键与方法:(1)关键:抓住互化公式π rad=180°是关键;(3)角度化弧度时,应先将分、秒化成度,再化成弧度;(4)角度化为弧度时,其结果写成π的形式,没特殊要求,切不可进行近似计算,也不必将π化为小数;(5)注意角度制和弧度制不能混用,如α=2kπ+45°,k∈Z,β=k·360°+ ,k∈Z都是不正确的写法.
(1)将α1,α2用弧度表示出来,并指出它们是第几象限角;(2)将β1,β2用角度表示出来,并在-720°~0°范围内,找出与它们有相同终边的所有角.
用弧度表示角及其范围例3用弧度表示终边落在下列各图所示阴影部分内(不包括边界)的角的集合.分析:先将边界角由角度化为弧度,再根据阴影部分写出角的集合.
反思感悟 用弧度制表示角应注意的问题:(1)用弧度表示区域角,实质是角度表示区域角在弧度制下的应用,必要时,需进行角度与弧度的换算.注意单位要统一,角度数与弧度数不能混用.(2)在表示角的集合时,可以先写出一周范围(如-π~π,0~2π)内的角,再加上2kπ,k∈Z.
变式训练3以弧度为单位,写出终边落在直线y=-x上的角的集合.
弧长公式与面积公式的应用例4(1)已知扇形的周长为8 cm,圆心角为2,求该扇形的面积;(2)已知扇形的周长为10 cm,面积等于4 cm2,求其圆心角的弧度数.分析:(1)先求出扇形的半径,再求面积;(2)设出圆心角,建立方程组求解.
反思感悟 弧度制下有关弧长、扇形面积问题的解题策略(1)扇形的弧长公式和面积公式涉及四个量:面积S,弧长l,圆心角α,半径r,已知其中的三个量一定能求得第四个量(通过方程求得),已知其中的两个量能求得剩余的两个量(通过方程组求得).(2)在研究有关扇形的相关量的最值时,往往转化为二次函数的最值问题.(3)注意扇形圆心角弧度数的取值范围是0<θ<2π,实际问题中注意根据这一范围进行取舍.
延伸探究 本例(1)中,将条件“圆心角为2”去掉,求扇形面积的最大值.解:设扇形的弧长为l cm,半径为r cm,则有2r+l=8,于是l=8-2r,故当半径为2 cm,圆心角为2时,扇形面积最大值为4 cm2.
混用角度制与弧度制致误
两个错解分别错在什么地方?你能发现吗?怎样避免这类错误呢?提示:两个错解都是由于混用了角度和弧度.正解:因为与45°角终边相同的角的集合为{α|α=k·360°+45°,k∈Z},
防范措施 在解决角度制和弧度制的有关问题时,要遵循转换的原则,表达的形式要符合基本的原则和规范性,即在同一个式子中角度制和弧度制不能混用.
1.1 920°转化为弧度数是( )答案:D
高考复习4.1 任意角和弧度制及三角函数的概念课件PPT: 这是一份高考复习4.1 任意角和弧度制及三角函数的概念课件PPT,共38页。PPT课件主要包含了象限角,圆心角,半径长,α·r,答案D,答案C,答案B,答案ABD,答案四等内容,欢迎下载使用。
数学必修41.1 任意角和弧度制课前预习ppt课件: 这是一份数学必修41.1 任意角和弧度制课前预习ppt课件,共50页。PPT课件主要包含了栏目导航,自主预习学案,互动探究学案,课时作业学案等内容,欢迎下载使用。
2022版高考数学一轮复习PPT课件:任意角、弧度制及任意角的三角函数: 这是一份2022版高考数学一轮复习PPT课件:任意角、弧度制及任意角的三角函数,共52页。PPT课件主要包含了栏目导航,课堂题型全突破,真题自主验效果,课前知识全通关,课后限时集训,象限角,象限角与终边相同的角,面积公式,三角函数的定义等内容,欢迎下载使用。













