高中数学苏教版必修13.4.1 函数与方程教学演示课件ppt

这是一份高中数学苏教版必修13.4.1 函数与方程教学演示课件ppt，共19页。PPT课件主要包含了x1-1x23，x1x21，无实数根，一个交点10，没有交点，判别式Δ，没有实数根，x10，等价关系，不是二重零点等内容，欢迎下载使用。

学习目标：1.知识目标：理解函数零点的意义，能判断二次函数零点的存在性，会求简单函数的零点，了解函数的零点与方程根的关系。2.能力目标：体验函数零点概念的形成过程，提高数学知识的综合应用能力。3.情感目标：让学生初步体会事物间相互转化的辩证思想。学习重点：函数零点的概念及求法学习难点：利用函数的零点作图
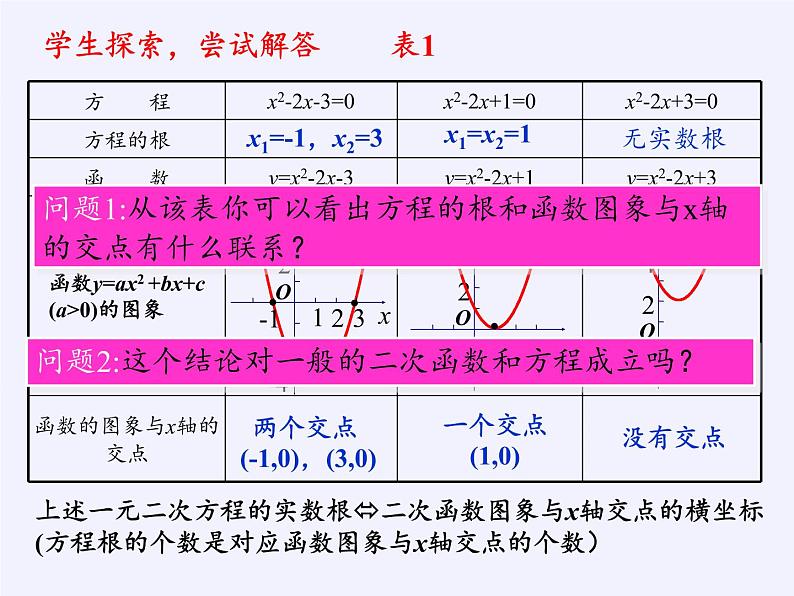
上述一元二次方程的实数根二次函数图象与x轴交点的横坐标(方程根的个数是对应函数图象与x轴交点的个数）
学生探索，尝试解答 表1
两个交点 (-1,0)，(3,0)
问题1:从该表你可以看出方程的根和函数图象与x轴的交点有什么联系？
问题2:这个结论对一般的二次函数和方程成立吗？
结论：一元二次方程的实数根就是相应二次函数图象与x轴交点的横坐标．
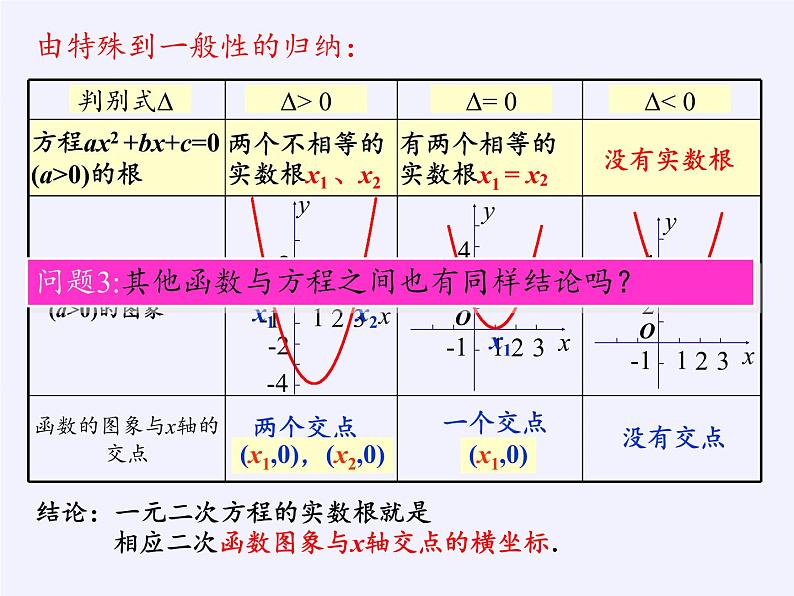
由特殊到一般性的归纳：
方程ax2 +bx+c=0(a>0)的根
两个不相等的实数根x1 、x2
有两个相等的实数根x1 = x2
(x1,0)，(x2,0)
问题3:其他函数与方程之间也有同样结论吗？
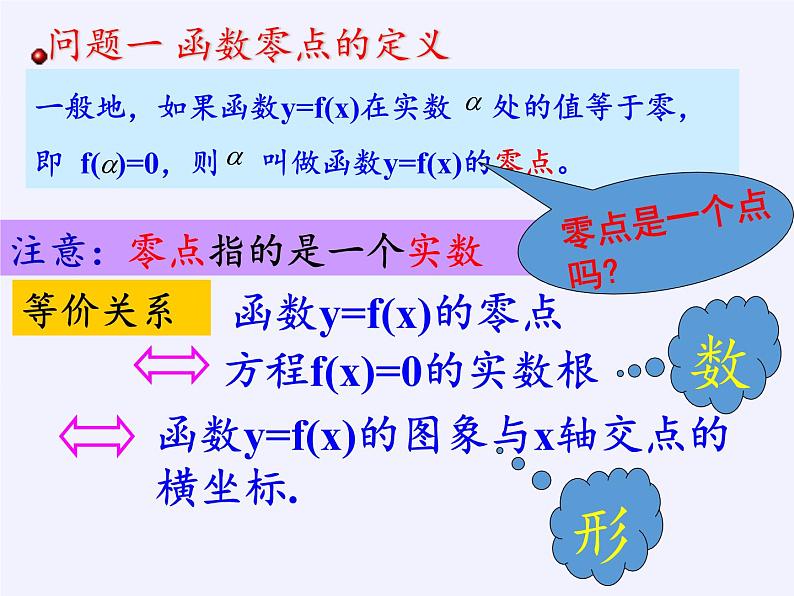
一般地，如果函数y=f(x)在实数 处的值等于零，即 f( )=0，则 叫做函数y=f(x)的零点。
问题一 函数零点的定义
注意：零点指的是一个实数
函数y=f(x)的零点
方程f(x)=0的实数根
函数y=f(x)的图象与x轴交点的横坐标.
思考？？问题二 如何求函数的零点
（1）（代数法）令f(x)=0，求方程的根；（2）（图象法）找出函数图象与x轴交点的横坐标。
小试牛刀：（1）.函数f(x)=x(x2－4)的零点为（ ）A．(0，0)，(2，0) B．0，2 C．(–2，0)，(0，0)，(2，0) D．–2，0，2（2）
问题三 如何判定二次函数y=ax2+bx+c的 零点个数？
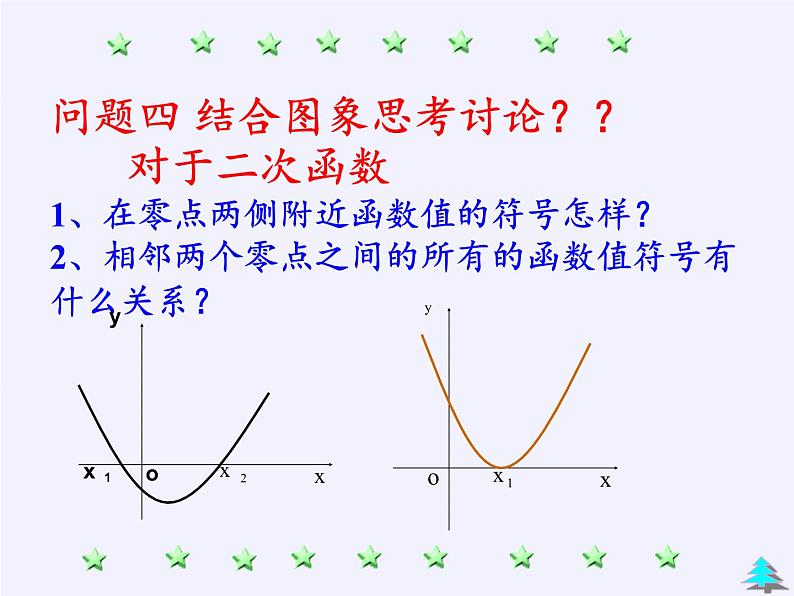
问题四 结合图象思考讨论？？ 对于二次函数1、在零点两侧附近函数值的符号怎样？2、相邻两个零点之间的所有的函数值符号有什么关系？
1、当函数的图象通过零点且穿过x轴时（ ），函数值变号。
2、相邻两个零点之间的所有函数值保持同号。
猜想：二次函数有这样的性质对任意函数是否有同样的性质？
结论：对任意函数，只要它 的图象是连续不间断的，上述性质同样成立
小试牛刀：求函数 的零点，并指出自变量x在什么范围内取值时，函数值y大于0？小于0？
解：令y=0得： 即 函数的零点为-8,1 函数图象如图 当x<-8或x>1时，y>0; 当-8例 求函数y=x3－2x2－x+2的零点，并画出它的图象
解：因为x3－2x2－x+2=x2(x－2)－(x－2) =(x－2)(x+1)(x－1). 所以函数的零点为－1，1，2.
3个零点把x轴分成4个区间：(－∞，－1)、(－1，1)、(1，2)、(2，+∞)。在这四个区间内，取x的一些值，以及零点，列出这个函数的对应值表：
在直角坐标系内描点连线，这个函数的图象如图所示
规律方法： 1、函数零点的求法： 2、解三次以上的高次方程，一般方法是
重要数学思想：函数与方程思想；转化与化归思想
3、作图步骤：（１）求零点 （２）划区间（３）列表取值（４）描点连线
2.函数y=-x2-2x+3的自变量在什么范围内取值时，函数值大于0、小于0、等于0？
通过本节课的学习你学到了哪些数学知识？又学到了哪些重要的数学思想？
1.函数零点的定义（三个等价关系）
数学思想：函数与方程思想；数形结合思想； 转化与化归思想
3. 二次函数零点个数的判定4.零点的性质
1．y＝x－2的图象与x轴的交点坐标及其零点分别是(　)A．2；2　　B．(2,0)；2C．－2；－2 D．(－2,0)；－22.二次函数 ，其中 ，则函数的零点有 个。3.已知函数 有两个零点，则 的取值范围为
课后思考？若函数 在区间 上存在唯一的零点，则 与 的符号会有怎样的关系？