


人教版八年级上册13.4课题学习 最短路径问题图片ppt课件
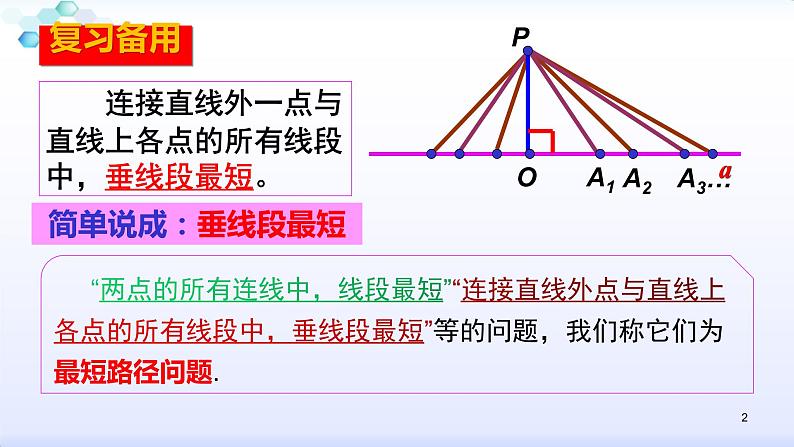
展开连接直线外一点与直线上各点的所有线段中,垂线段最短。
“两点的所有连线中,线段最短”“连接直线外点与直线上各点的所有线段中,垂线段最短”等的问题,我们称它们为最短路径问题.
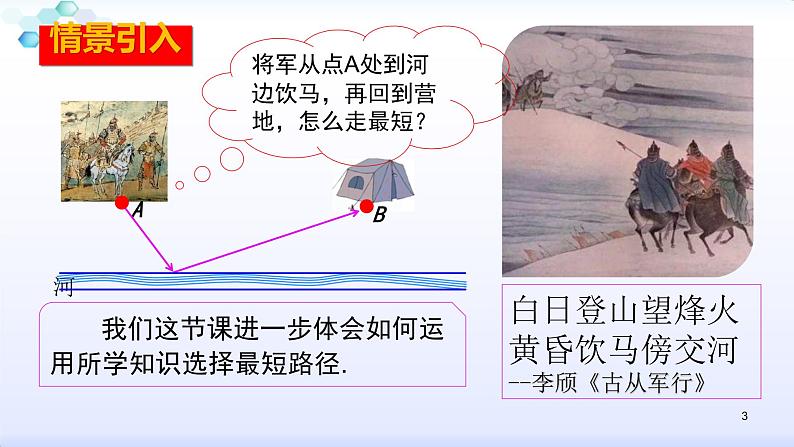
白日登山望烽火黄昏饮马傍交河--李颀《古从军行》
我们这节课进一步体会如何运用所学知识选择最短路径.
将军从点A处到河边饮马,再回到营地,怎么走最短?
第十三章 轴对称
13.4 课题学习 最短路径问题
1.能说出轴对称的相关概念及其性质.2.能利用轴对称变换解决日常生活中的最短路径问题.
重点:利用轴对称变换解决日常生活中的最短路径问题.难点:将实际问题中的最短路径问题转化为数学知识解决.
知识点一:利用轴对称解决最短路径问题
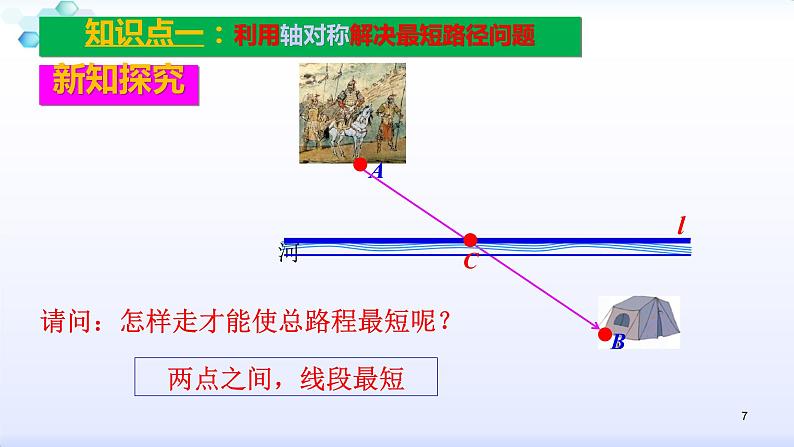
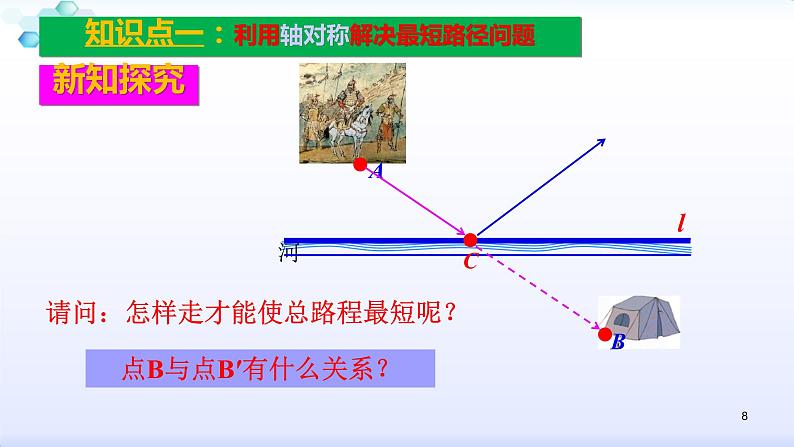
问题1:(将军饮马问题)如图将军从A地出发,到一条笔直的河边l饮马,然后回到B地,将军到河边什么地方饮马,可使所走的路径最短?
请问:怎样走才能使总路程最短呢?
点B与点B′有什么关系?
例1:已知:直线l和同侧两点A、B
求作:直线l上一点C满足AC+BC的值最小.
作法: 1、作点B关于直线l的对称点B'
2、连接AB' ,交直线l于C 。
1.如图,在△ABC中,AB=3,AC=4,EF垂直平分线段BC,点P是直线EF上的任一点,则AP+BP的最小值是( )A.4 B. 5 C.6 D.72.如图,E是正方形ABCD的边AB上的一点,AE=3,BE=1,P是AC上一动点,则当PB+PE为最小值时,点P为( )A.AC的三等分点 B.AC的中点C.连接DE与AC的交点 D.以上都不对
3.如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为 .4.如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为( )A.4 B.5 C.6 D.7
例2:如图,已知点A是锐角∠MON内的一点,试分别在OM,ON上确定点B,C,使△ABC的周长最小,写出你作图的主要步骤,并标明你所确定的点.(要求画出草图,保留作图痕迹)
作法: 1、分别作点A关于OM、ON的对称点A′,A′′;
2、连接A′A′′ ,分别交OM、ON于B、C ;
1.如图,在直角坐标系中,点A,B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是( )A.(0,0) B.(0,1) C.(0,2) D.(0,3)
2.如图,OA,OB分别是线段MC,MD的垂直平分线,MD=5cm,MC=7cm,CD=10cm,一只小蚂蚁从点M出发爬到OA边上任意一点E,再爬到OB边上任意一点F,然后爬回M点处,则小蚂蚁爬行的路径最短可为( )A. 12cm B 10cm C. 7cm D. 5cm
例3:某中学八(12)班举行文艺晚会,桌子摆成如图所示两直排(图中的AO,BO),AO桌面上摆满了橘子,OB桌面上摆满了糖果,站在C处的学生小明先拿橘子再拿糖果,然后到D处座位上,请你帮助他设计一条行走路线,使其所走的总程最短.
先独立完成导学案互动探究3,再同桌相互交流,最后小组交流;
直线l上找一点C,使AC+BC的值最小.
作点B关于直线l的对称点B',连接AB' ,交直线l于C ,则点C即为所求。
通过轴对称把直线同侧的两点到直线上一点距离的和最短的问题转化为两点间距离最短问题.
在直线l1和直线l2上分别找点M,N,使△PMN的周长最小.
过点P分别作关于直线l1和l2的对称点P′,P",连接P′P′′分别交l1和l2于点M,N,则点M,N即为所求
通过轴对称把周长最小问题转化为两点间距离最短问题,△PMN周长的最小值为MP+MN+NP=P′P′′,依据是两点之间,线段最短.
通过轴对称把周长最小问题转化为两点间距离最短问题,四边形PQMM周长的最小值为MP+PQ+NQ+MN=P′Q′+PQ,依据是两点之间,线段最短.
在直线l1和直线l2上分别找点M,N,使四边形PQNM的周长最小.
分别作点P,Q关于直线l1和l2的对称点P′,Q′,连接P′Q′分别交l1和l2于点M,N,则点M,N即为所求.
知识点二:利用平移解决最短路径问题
问题2:(造桥选址问题)如图,A和B两地在一条河的两岸,现要在河上造一座桥MN,桥造在何处可使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)
由于河岸宽度是固定的,因此当AM+NB最小时,AM+MN+NB最小.这样,问题就进一步转化为:当点N在直线b的什么位置时,AM+NB最小? 能否通过图形的变化(轴对称、平移等),把这个问题转化为像前面的两点之间线段最短问题呢?
如图,假设桥建在M′N′处,将AM′沿与河岸垂直的方向平移,点M′移动到点N′,点A移动到点A′,则AA′=M′N′,AM′+N′B=A′N+NB.这样,问题就转化为:当点N在直线b的什么位置时,A′N+NB最小?
如图,在连接A′,B两点的线中,线段A′B最短.因此,线段A′B与直线b的交点N的位置即为所求,即在点N处造桥MN,所得路径AMNB是最短的.
你能证明AMNB最短吗?
在解决最短路径问题时,我们通常利用轴对称、平移等变化把已知问题转化为容易解决的问题,从而作出最短路径的选择.
知识点三:利用轴对称和垂线段最短解决最小值问题
例4:如图,在锐角三角形ABC中,AC=6,△ABC的面积为15.∠BAC的平分线交BC于点D,点M,N分别是AD和AB上的动点,则BM+MN的最小值是 .
BE的长就是BM+MN的最小值
1.如图,△ABC是等边三角形,高AD=3,点E是AB上的动点,点P是AD上的动点,则PE+PB的最小值为 .
2.在所给网格图(每小格均为边长是1的正方形)中完成下列各题(用直尺画图):(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;(2)在DE上画出点P,使PB1+PC最小;(3)在DE上画出点Q,使QA+QC最小
利用轴对称、平移变换将问题转化为容易解决的问题.
对自己说,你有什么收获? 对同学说,你有什么温馨提示? 对老师说,你还有什么困惑?
2021学年13.4课题学习 最短路径问题教学ppt课件: 这是一份2021学年13.4课题学习 最短路径问题教学ppt课件,共19页。PPT课件主要包含了导入--原题再现,题目解析,变式训练,中考链接,拓展提升,分析讲解,做对称,问题剖析,将军饮马的12种模型,最短路径--小结等内容,欢迎下载使用。
初中人教版13.4课题学习 最短路径问题课前预习课件ppt: 这是一份初中人教版13.4课题学习 最短路径问题课前预习课件ppt,共16页。
数学八年级上册13.4课题学习 最短路径问题试讲课教学课件ppt: 这是一份数学八年级上册13.4课题学习 最短路径问题试讲课教学课件ppt,共16页。PPT课件主要包含了将军饮马问题等内容,欢迎下载使用。













