初中数学人教版八年级上册12.1 全等三角形同步达标检测题

人教版2021年八年级上册第12章《全等三角形》单元训练卷

一．选择题

1．下列判断正确的是（　　）

A．形状相同的图形叫全等形 

B．图形的面积相等的图形叫全等形 

C．部分重合的两个图形全等 

D．两个能完全重合的图形是全等形

2．如图是两个全等三角形，则∠1的度数为（　　）

A．48° B．60° C．62° D．72°

3．在测量一个小口圆形容器的壁厚时，小明用“X型转动钳”按如图方法进行测量，其中OA＝OD，OB＝OC，测得AB＝5厘米，EF＝6厘米，圆形容器的壁厚是（　　）

A．5厘米 B．6厘米 C．2厘米 D．厘米

4．如图，已知三角形ABC与三角形DEF是全等形，则相等的线段有（　　）

A．1组 B．2组 C．3组 D．4组

5．已知：如图，点D，E分别在AC，AB上，AB＝AC，添加一个条件，不能判定△ABD≌△ACE的是（　　）

A．BD＝CE B．AD＝AE C．∠B＝∠C D．∠ADB＝∠AEC

6．已知，△ABC≌△DEF，且△ABC的周长为20，AB＝8，BC＝3，则DF等于（　　）

A．3 B．5 C．9 D．11

7．如图，直线l1、l2、l3分别表示三条相互交叉的公路，现要建立一个货物中转站，要求它到三条公路的距离相等，则可选择的地址有（　　）

A．一处 B．二处 C．三处 D．四处

8．如图，△ABC≌△AED，点D在BC上，若∠EAB＝42°，则∠DAC的度数是（　　）

A．48° B．44° C．42° D．38°

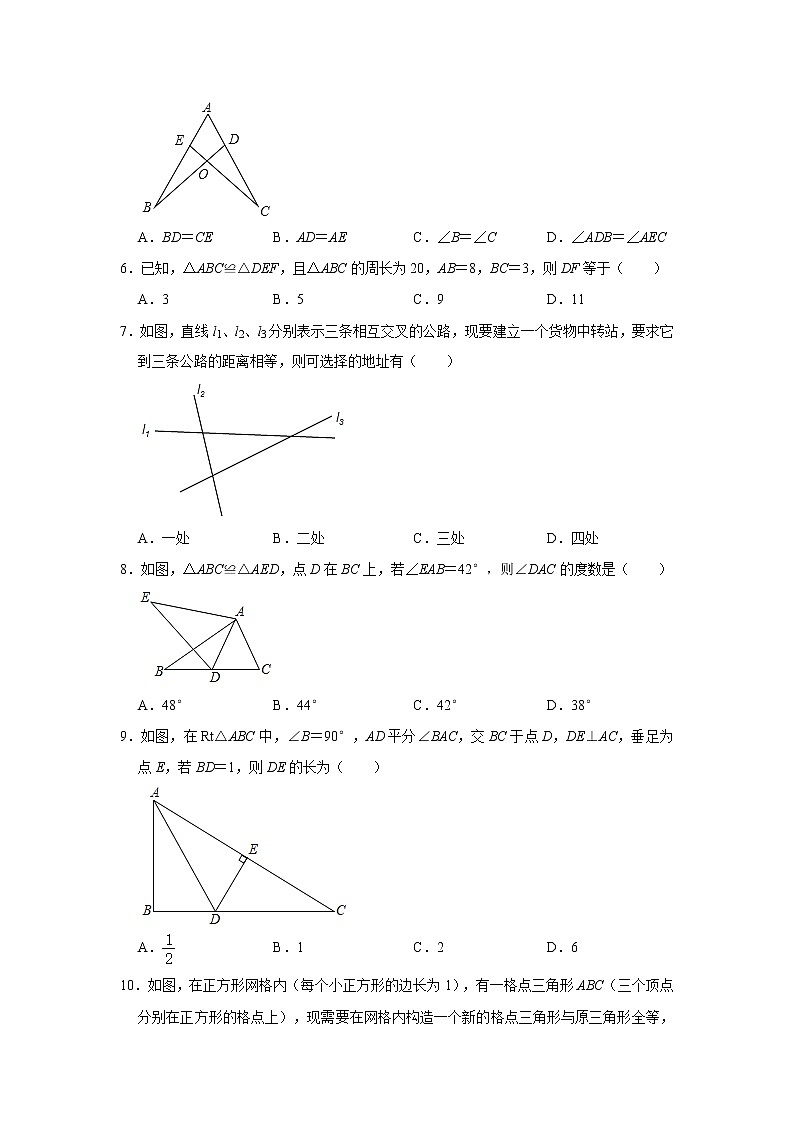
9．如图，在Rt△ABC中，∠B＝90°，AD平分∠BAC，交BC于点D，DE⊥AC，垂足为点E，若BD＝1，则DE的长为（　　）

A． B．1 C．2 D．6

10．如图，在正方形网格内（每个小正方形的边长为1），有一格点三角形ABC（三个顶点分别在正方形的格点上），现需要在网格内构造一个新的格点三角形与原三角形全等，且有一条边与原三角形的一条边重合，这样的三角形可以构造出（　　）

A．3个 B．4个 C．5个 D．6个

二．填空题

11．如图，要测量河岸相对的两点A、B之间的距离，已知AB垂直于河岸BF，现在BF上取两点C、D，使CD＝CB，过点D作BF的垂线ED，使点A、C、E在一条直线上，若ED＝65米，则AB的长是 　    　．

12．如图，在△ABC中，∠ACB＝90°，AD平分∠CAB交BC于点D，且BD＝2CD，BC＝9cm．则点D到AB的距离为 　    　．

13．如图，AC平分∠DCB，CB＝CD，DA的延长线交BC于点E，若∠BAE＝80°，则∠EAC的度数为　    　．

14．如图是由6个边长相等的正方形组合成的图形，∠1+∠2+∠3＝　     　．

15．如图，AB＝12m，CA⊥AB于A，DB⊥AB于B，且AC＝4m，P点从B向A运动，每分钟走1m，Q点从B向D运动，每分钟走2m，P、Q两点同时出发，运动 　 　分钟后，△CAP与△PQB全等．

16．已知，△ABC中，∠BAC＝120°，AD平分∠BAC，∠BDC＝60°，AB＝2，AC＝3，则AD的长是　 　 　．

三．解答题

17．如图，已知OA＝OC，OB＝OD，∠AOC＝∠BOD．

求证：△AOB≌△COD．

18．如图，已知AD＝AE，∠B＝∠C．求证：△ACD≌△ABE．

19．如图，点A、B、C、D在同一直线上，△ACE≌△DBF，AD＝8，BC＝2．

（1）求AC的长；

（2）求证：CE∥BF，AE∥DF．

20．如图，CD⊥AB于点D，BE⊥AC于点E，△ABE≌△ACD，∠C＝42°，AB＝9，AD＝6，G为AB延长线上一点．

（1）求∠EBG的度数．

（2）求CE的长．

21．如图，OC平分∠MON，P为OC上一点，PA⊥OM，PB⊥ON，垂足分别为A，B，连接AB，AB与OP交于点E．

（1）求证：△OPA≌△OPB；

（2）若AB＝6，求AE的长．

22．如图，在△ABC中，∠CAB＝60°，∠CAB的平分线AP与∠CBA的平分线BP相交于点P，连接CP．

（1）求证：CP平分∠ACB；

（2）若AP＝4，△ABC的周长为20，求△ABC的面积．

23．在Rt△ABC中，∠C＝90°，AC＝8cm，BC＝6cm，点D在AC上，且AD＝6cm，过点A作射线AE⊥AC（AE与BC在AC同侧），若动点P从点A出发，沿射线AE匀速运动，运动速度为1cm/s，设点P运动时间为t秒．连接PD、BD．

（1）如图①，当PD⊥BD时，求证：△PDA≌△DBC；

（2）如图②，当PD⊥AB于点F时，求此时t的值．

参考答案

一．选择题

1．解：A、如果形状相同而面积不同，则不是全等形，错；

B、如果面积相等，而形状不同，则不是全等形，错；

C、根据全等形概念，强调是完全重合，错．

D、正确．

故选：D．

2．解：∵∠B＝48°，∠C＝60°，

∴∠A＝180°﹣48°﹣60°＝72°，

∵两个三角形全等，

∴∠1＝∠A＝72°，

故选：D．

3．解：连接AB．

在△AOB和△DOC中，

，

∴△AOB≌△DOC（SAS），

∴AB＝CD＝5厘米，

∵EF＝6厘米，

∴圆柱形容器的壁厚是×（6﹣5）＝（厘米），

故选：D．

4．解：∵三角形ABC与三角形DEF是全等形，

∴AB＝DE，AC＝DF，BC＝EF，

∵BC＝EF即BE+EC＝CF+EC

∴BE＝CF

∴共有AB＝DE，AC＝DF，BC＝EF，BE＝CF4组．

故选：D．

5．解：已知条件中AB＝AC，∠A为公共角，

A．若添加BD＝CE，已知两边及一边所对的角，则不能证明△ABD≌△ACE，故A选项合题意．；

B．若添加AD＝AE，可利用SAS定理可证明△ABD≌△ACE，故B选项不合题意；

C．若添加∠B＝∠C，可利用ASA定理可证明△ABD≌△ACE，故C选项不合题意；

D．若添加∠ADB＝∠AEC，可利用AAS定理可证明△ABD≌△ACE，故D选项不合题意；

故选：A．

6．解：∵△ABC的周长为20，AB＝8，BC＝3，

∴AC＝20﹣3﹣8＝9，

∵△ABC≌△DEF，

∴DF＝AC＝9，

故选：C．

7．解：如图，可选择的地址有四处．

故选D．

8．解：∵△ABC≌△AED，

∴∠EAD＝∠BAC，

∴∠EAB＝∠DAC＝42°．

故选：C．

9．解：∵AD平分∠BAC交BC于点D，DE⊥AC，DB⊥AB，

∴DE＝DB＝1．

故选：B．

10．解：如图满足条件的三角形如图所示，有5个．

故选：C．

二．填空题

11．解：∵AB⊥BD，ED⊥AB，

∴∠ABC＝∠EDC＝90°，

在△ABC和△EDC中，

，

∴△ABC≌△EDC（ASA），

∴AB＝ED＝65（米）．

故答案为：65米．

12．解：过D点作DE⊥AB于E，如图，

∵AD平分∠CAB，DC⊥AC，DE⊥AB，

∴DE＝DC，

∵BD＝2CD，BC＝9cm，

∴CD＝BC＝3cm，

∴DE＝3cm，

即点D到AB的距离为3cm．

故答案为3cm．

13．解：∵AC平分∠DCB，

∴∠BCA＝∠DCA，

在△ABC和△ADC中，

，

∴△ABC≌△ADC（SAS），

∴∠B＝∠D，

∴∠B+∠BCA＝∠D+∠DCA，

∵∠EAC＝∠D+∠DCA，

∴∠B+∠BCA＝∠EAC，

∵∠B+∠BCA＝180°﹣∠BAC＝180°﹣∠BAE﹣∠EAC，

∴∠CAE＝180°﹣∠BAE﹣∠EAC，

∵∠BAE＝80°，

∴∠EAC＝50°，

故答案为：50°．

14．解：如图，

根据题意得DE＝BC，EC＝AB，GF＝GC，∠DEC＝∠ABC＝∠FGC＝90°，

∴△CGF为等腰直角三角形，

∴∠2＝45°，

在△ABC和△CED中，

，

∴△ABC≌△CED（SAS），

∴∠1＝∠DCE，

∵∠DCE+∠3＝90°，

∴∠1+∠3＝90°，

∴∠1+∠2+∠3＝90°+45°＝135°．

故答案为135°．

15．解：∵CA⊥AB于A，DB⊥AB于B，

∴∠A＝∠B＝90°，

设运动x分钟后△CAP与△PQB全等；

则BP＝xm，BQ＝2xm，则AP＝（12﹣x）m，

分两种情况：

①若BP＝AC，则x＝4，

AP＝12﹣4＝8，BQ＝8，AP＝BQ，

∴△CAP≌△PBQ；

②若BP＝AP，则12﹣x＝x，

解得：x＝6，BQ＝12≠AC，

此时△CAP与△PQB不全等；

综上所述：运动4分钟后△CAP与△PQB全等；

故答案为：4．

16．解：过点D作DH⊥AC于H，DG⊥AB，交AB的延长线于G，

∵AD平分∠BAC，DH⊥AC，DG⊥AB，

∴DH＝DG，

∵∠BAC＝120°，∠BDC＝60°，

∴∠C+∠ABD＝360°﹣120°﹣60°＝180°，

∵∠ABD+∠DBG＝180°，

∴∠C＝∠DBG，

在△DCH和△DBG中，

，

∴△DCH≌△DBG（AAS），

∴HC＝BG，

∵AD平分∠CAB，

∴∠CAD＝∠BAD，

在△ADH和△ADG中，

，

∴△ADH≌△ADG（AAS），

∴AH＝AG，

∴AC﹣CH＝AB+BG，

∴3﹣CH＝2+CH，

∴CH＝，

∴AH＝，

∵∠ADH＝30°，

∴AD＝2AH＝5，

故答案为：5．

三．解答题

17．证明：∵∠AOC＝∠BOD，

∴∠AOC﹣∠AOD＝∠BOD﹣∠AOD，

即∠COD＝∠AOB，

在△AOB和△COD中，

，

∴△AOB≌△COD（SAS）．

18．证明：在△ACD和△ABE中，

，

∴△ACD≌△ABE（AAS）．

19．解：（1）∵△ACE≌△DBF，

∴AC＝DB，

∵AC+BD＝AD+BC，

∴2AC＝AD+BC，

∵AD＝8，BC＝2，

∴2AC＝8+2＝10，

∴AC＝5；

（2）∵△ACE≌△DBF，

∴∠ECA＝∠FBD，∠A＝∠D，

∴CE∥BF，AE∥DF．

20．解：（1）∵△ABE≌△ACD，

∴∠EBA＝∠C＝42°，

∴∠EBG＝180°﹣42°＝138°；

（2）∵△ABE≌△ACD，

∴AC＝AB＝9，AE＝AD＝6，

∴CE＝AC﹣AE＝9﹣6＝3．

21．（1）证明：∵PA⊥OM，PB⊥ON，OC平分∠MON，

∴∠PAO＝∠PBO＝90°，PA＝PB，

在Rt△OPA和Rt△OPB中，

，

∴Rt△OPA≌Rt△OPB（HL）；

（2）解：由（1）知△OPA≌△OPB，

∴∠APE＝∠BPE，

又∵PA＝PB，

在△APE和△BPE中，

，

∴△APE≌△BPE（SAS），

∴AE＝BE，

∴AE＝AB，

∵AB＝6，

∴AE＝3．

22．（1）证明：过点P作PD⊥AB于D，作PE⊥BC于E，作PF⊥AC于F，

则PD，PE，PF分别是P到AB，BC，CA的距离，

∵AP平分∠CAB，BP平分∠ABC，

∴PD＝PF，PD＝PE，

∴PF＝PE，

∴CP平分∠ACB；

（2）解：∵∠CAB＝60°，

∴∠PAB＝30°，

在Rt△PAD中，PA＝4，

∴PD＝2，

∴S△ABC＝S△APB+S△BPC+S△CPA

＝AB•PD+BC•PE+CA•PF

＝（AB+BC+CA）•PD

＝×20×2

＝20．

23．（1）证明：如图①，∵PD⊥BD，

∴∠PDB＝90°，

∴∠BDC+∠PDA＝90°，

又∵∠C＝90°，

∴∠BDC+∠CBD＝90°，

∴∠PDA＝∠CBD，

又∵AE⊥AC，

∴∠PAD＝90°，

∴∠PAD＝∠C＝90°，

又∵BC＝6cm，AD＝6cm，

∴AD＝BC，

在△PAD和△DCB中，

，

∴△PDA≌△DBC（ASA）；

（2）解：如图②，∵PD⊥AB，

∴∠AFD＝∠AFP＝90°，

∴∠PAF+∠APF＝90°，

又∵AE⊥AC，

∴∠PAF+∠CAB＝90°，

∴∠APF＝∠CAB，

在△APD和△CAB中，

，

∴△APD≌△CAB（AAS），

∴AP＝AC，

∵AC＝8cm，

∴AP＝8cm，

∴t＝8．