






初中鲁教版 (五四制)1 对函数的再认识图片课件ppt
展开1.会根据实际问题求出函数的关系式;2.了解对应观点下的函数意义;3.会求简单的函数值。
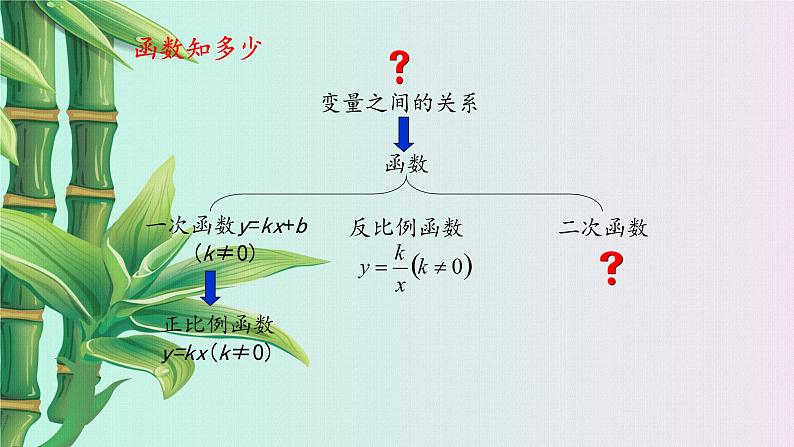
一次函数y=kx+b (k≠0)
正比例函数y=kx(k≠0)
(1)A、B两地之间的路程为900km,一辆汽车从A地到B地所需时间t(h)与汽车的平均速度v(km/h)之间的关系式是_____________ 。(2)矩形ABCD的面积为18cm2,其中一边BC长为acm,矩形ABCD的周长c(cm)与a(cm)的关系式是_____________。
c=2(a+18/a)
(3)某种书定价8元,若购书不超过10本,按原价付款;若一次购书10本以上,超过10本部分打八折。1.购买该种书6本需付款 元;2.购买该种书14本需付款 元;3.付款金额y元与购买该种书的本数x(本)之间的关系式是: y={
y=8x (x≤10)
y=80+8×80%(x-10) (x>10)
(1)自变量分别是什么?自变量可以取值的范围是什么?(2)对于自变量在它可以取值的范围内的每一个值,另一个变量是否都有唯一确定的值与它对应?(3)由此你对函数有了哪些进一步的认识?与同伴进行交流。
问题探究一:函数的意义
一般地,如果在一个变化过程中,有两个变量x和y,并且对于自变量x在某一范围内的每一个确定值,变量y都有唯一确定的值与它对应,那么我们称y是x的函数,其中x是自变量,y是因变量。
下列表达式是否为函数?(1)y=±x(2)y=x2(3)s=t3+2(4)y=x+2
下列图象能表示y是x的函数是( )
例1:如图,正方形ABCD的边长为2,点P为AD边上一点,设AP=x,四边形BCDP的面积为y,求y与x之间的函数关系式,并指出x的取值范围。
分析:S△APB+S四边形BCDP=S正方形ABCD,S△APB如何用x来表示?
S△APB+S四边形BCDP=S正方形ABCDS△APB=xS正方形ABCD=4所以S四边形BCDP=4-x 即y=4-x又因为P在AD边上,所以0
问题探究二:理解函数值,会求函数值
对于自变量x在可以取值范围内的一个确定的值α,函数y有唯一确定的对应值,这个对应值叫做 。如对于例2(1)中的函数y=3x+7,16就是当x =3时的函数值。
1.教科书随堂练习1、2。2.目前,全球淡水资源日益减少,提倡全社会节约用水。据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升。小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x分钟后,水龙头滴出y毫升的水,请写出y与x之间的函数关系式是( )。 A.y=0.05x B.y=5x C.y=100x D.y=0.05x+100
3.将完全相同的平行四边形和完全相同的菱形镶嵌成如图所示的图案。设菱形中较小角为x度,平行四边形中较大角为y度,则y与x的关系式是( )。
习题3.1,1、2题。
请你从下面的实例体会表示函数的方法:
(1)某届全国图书展销会于5月份举行。本届书市总收入约1800万元(包括零售和批发),其中零售收入约500万元,展销会期间的零售收入统计如下:
用表格表示函数的方法称为列表法
(2)如图是某气象站用自动温度记录仪扫描出的某一天气温变化情况的曲线。它直观地反映了温度T和时间t间的对应关系。根据图象信息,回答下列问题:①在这一天中,何时气温最高?何时气温最低?②气温T是时刻t的函数吗?它是用什么方法表示的?
用图象表示函数的方法称为图象法
表示函数的方法有哪几种?你能举例说明吗?与同伴进行交流。
用来表示函数关系的数学式子做函数表达式(或解析式),
函数还可以用表格和图象表示,分别称为列表法和图象法。
用数学式子表示函数的方法称为解析法。
你认为用解析法、列表法和图象法表示函数关系各有哪些优点?
解析法可以比较全面、完整、简洁地表示出变量之间的关系。 列表法可以清楚、直接地表示出变量之间的数值对应关系。 图象法可以直观地表示出函数的变化过程和变化趋势。
典型例题3 求下列函数的自变量的取值范围:
探究:如何求自变量的取值范围
根据函数解析式确定自变量的取值范围的规律
用总长为60m的篱笆围成矩形场地,求矩形的面积S(m2)与它的一边长x(m)之间的关系式,并求出x的取值范围。
那么,S与x之间的关系式为
如何确定函数自变量的取值范围呢?
函数自变量的取值范围,应使函数表达式有意义。在解决实际问题时,还必须考虑使实际问题有意义。
3.已知y关于x的函数图象如图所示,则当y>0时,自变量x的取值范围是( )。
函数的三种表示方法是:解析法、列表法、图象法
鲁教版 (五四制)九年级上册第三章 二次函数1 对函数的再认识精品课件ppt: 这是一份鲁教版 (五四制)九年级上册第三章 二次函数1 对函数的再认识精品课件ppt,文件包含鲁教版五四制数学九上《对函数的再认识2》课件pptx、鲁教版五四制数学九上《对函数的再认识2》教案doc等2份课件配套教学资源,其中PPT共14页, 欢迎下载使用。
鲁教版 (五四制)九年级上册1 对函数的再认识优质课课件ppt: 这是一份鲁教版 (五四制)九年级上册1 对函数的再认识优质课课件ppt,文件包含鲁教版五四制数学九上《对函数的再认识1》课件pptx、鲁教版五四制数学九上《对函数的再认识1》教案doc等2份课件配套教学资源,其中PPT共18页, 欢迎下载使用。
初中数学鲁教版 (五四制)九年级上册2 二次函数背景图ppt课件: 这是一份初中数学鲁教版 (五四制)九年级上册2 二次函数背景图ppt课件,共17页。PPT课件主要包含了教学目标,y3x,y2x-6,复习回顾,问题探究,新知讲解,课堂小结等内容,欢迎下载使用。













