2018-2019学年广东深圳福田区八上期末数学试卷

这是一份2018-2019学年广东深圳福田区八上期末数学试卷，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共12小题；共60分）
1. 下列实数中最大的是
A. −2B. 0C. 14D. 2

2. 下列几组数中，不能作为直角三角形三边的是
A. 1，2，3B. 7，24，25C. 4，5，6D. 35，45，1

3. 如图所示，直线 a，b，c，d 的位置如图所示，若 ∠1=115∘，∠2=115∘，∠3=124∘，则 ∠4 的度数为 ．
A. 56∘B. 60∘C. 65∘D. 66∘

4. 下列二次根式中，最简二次根式的是
A. 18B. 8C. 10D. 12

5. 已知点 M 向左平移 3 个单位长度后的坐标为 −1,2，则点 M 原来的坐标是
A. −4,2B. 2,2C. −1,3D. −1,−2

6. 在一次艺术作品制作比赛中，某小组八件作品的成绩（单位：分）分别是：7，9，8，9，8，10，9，7，下列说法不正确的是
A. 中位数是 8.5B. 平均数是 8.4C. 众数是 9D. 极差是 3

7. 以方程组 y=2x−4,3x+y=1 的解为坐标的点 x,y 在平面直角坐标系中的位置是
A. 第一象限B. 第二象限C. 第三象限D. 第四象限

8. 下列命题是假命题的是
A. 49 的平方根是 ±7
B. 点 M1,a 和点 N3,b 是一次函数 y=−2x+1 图象上的两点，则 a>b
C. 无限小数都是无理数
D. 点 −2,3 到 y 轴的距离是 2

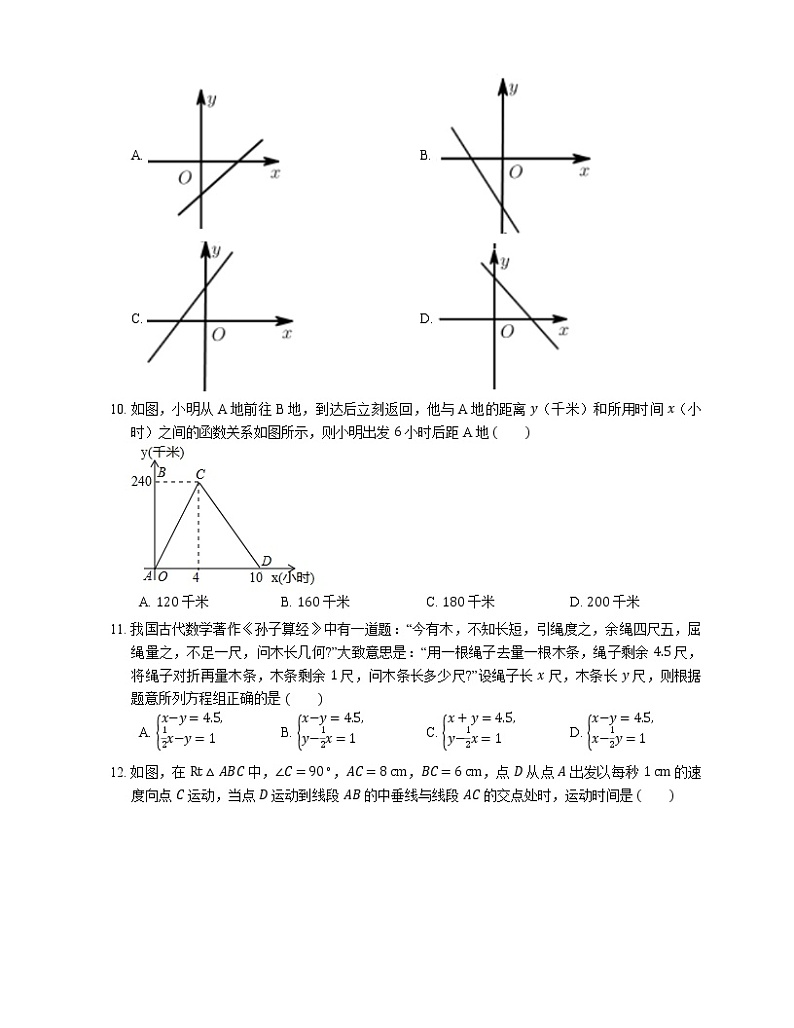
9. 一次函数 y=kx−kk<0 的图象大致是
A. B.
C. D.

10. 如图，小明从A地前往B地，到达后立刻返回，他与A地的距离 y（千米）和所用时间 x（小时）之间的函数关系如图所示，则小明出发 6 小时后距A地
A. 120 千米B. 160 千米C. 180 千米D. 200 千米

11. 我国古代数学著作《孙子算经》中有一道题：“今有木，不知长短，引绳度之，余绳四尺五，屈绳量之，不足一尺，问木长几何?”大致意思是：“用一根绳子去量一根木条，绳子剩余 4.5 尺，将绳子对折再量木条，木条剩余 1 尺，问木条长多少尺?”设绳子长 x 尺，木条长 y 尺，则根据题意所列方程组正确的是
A. x−y=4.5,12x−y=1B. x−y=4.5,y−12x=1C. x+y=4.5,y−12x=1D. x−y=4.5,x−12y=1

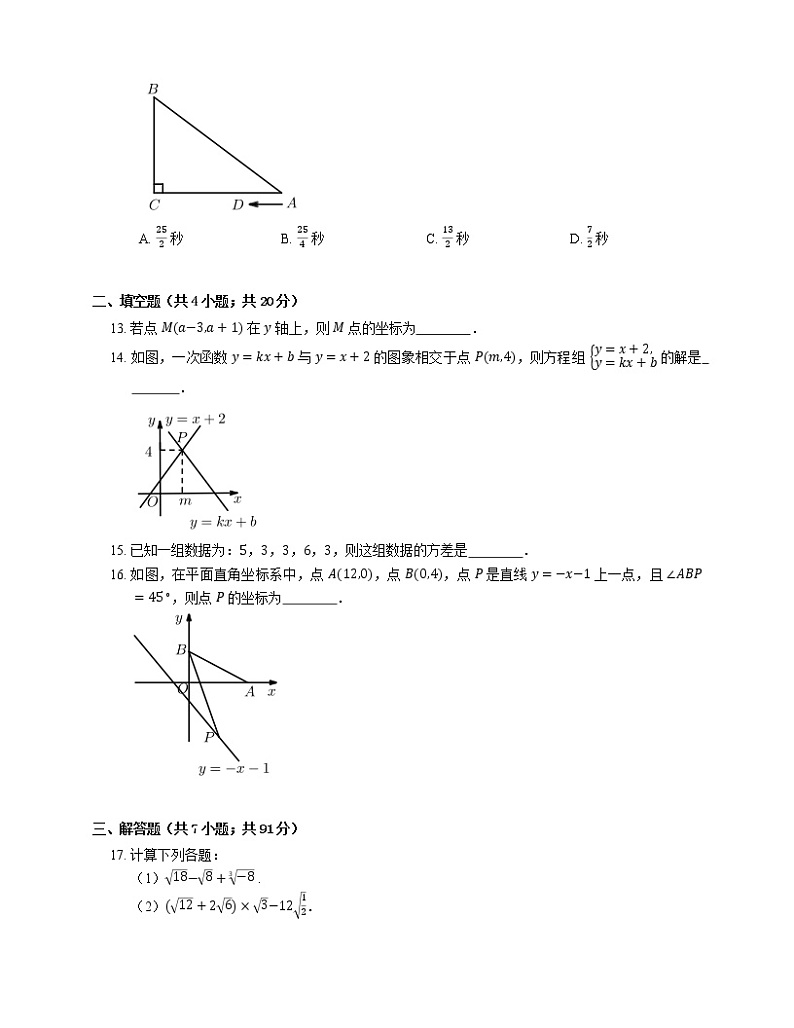
12. 如图，在 Rt△ABC 中，∠C=90∘，AC=8 cm，BC=6 cm，点 D 从点 A 出发以每秒 1 cm 的速度向点 C 运动，当点 D 运动到线段 AB 的中垂线与线段 AC 的交点处时，运动时间是
A. 252 秒B. 254 秒C. 132 秒D. 72 秒

二、填空题（共4小题；共20分）
13. 若点 Ma−3,a+1 在 y 轴上，则 M 点的坐标为 ．

14. 如图，一次函数 y=kx+b 与 y=x+2 的图象相交于点 Pm,4，则方程组 y=x+2,y=kx+b 的解是 ．

15. 已知一组数据为：5，3，3，6，3，则这组数据的方差是 ．

16. 如图，在平面直角坐标系中，点 A12,0，点 B0,4，点 P 是直线 y=−x−1 上一点，且 ∠ABP=45∘，则点 P 的坐标为 ．

三、解答题（共7小题；共91分）
17. 计算下列各题：
（1）18−8+3−8 .
（2）12+26×3−1212．

18. 解方程组：2x−3y=5,3x+y=2.

19. 4 月 23 日是世界读书日，习近平总书记说：“读书可以让人保持思维活力，让人得到智慧的启发，让人漱养浩然正气．”倡导读书活动，鼓励师生利用课余时间广泛阅读．期末，学校为了调查这学期学生课外阅读情况，随机抽样调查了一部分学生阅读课外书的本数，并将收集到的数据整理成如图的统计图．
（1）这次一共调查的学生人数是 人．
（2）所调查学生读书本数的众数是 本，中位数是 本．
（3）若该校有 800 名学生，请你估计该校学生这学期读书总数是多少本?

20. 如图，已知点 E 在线段 AD 上，点 P 在直线 CD 上，∠AEF=∠F，∠BAD=∠CPF．求证：∠ABD+∠BDC=180∘．

21. 某一天，水果经营户老张用 1600 元从水果批发市场批发猕猴桃和芒果共 50 千克，后再到水果市场去卖，已知猕猴桃和芒果当天的批发价和零售价如表所示：
品名猕猴桃芒果批发价元/千克2040零售价元/千克2650
（1）他购进的猕猴桃和芒果各多少千克?
（2）如果猕猴桃和芒果全部卖完，他能赚多少钱?

22. 如图所示，在平面直角坐标系中，已知 A0,1，B2,0，C4,3．
（1）在平面直角坐标系中画出 △ABC，则 △ABC 的面积是 ．
（2）若点 D 与点 C 关于 y 轴对称，则点 D 的坐标为 ．
（3）已知 P 为 x 轴上一点，若 △ABP 的面积为 4，求点 P 的坐标．

23. 如图 1，在平面直角坐标系中将 y=2x+1 向下平移 3 个单位长度得到直线 l1，直线 l1 与 x 轴交于点 C；直线 l2：y=x+2 与 x 轴、 y 轴交于 A，B 两点，且与直线 l1 交于点 D．
（1）填空：点 A 的坐标为 ，点 B 的坐标为 ．
（2）直线 l1 的表达式为 ．
（3）在直线 l1 上是否存在点 E，使 S△AOE=2S△ABO?若存在，则求出点 E 的坐标；若不存在，请说明理由．
（4）如图 2，点 P 为线段 AD 上一点（不含端点），连接 CP，一动点 H 从 C 出发，沿线段 CP 以每秒 1 个单位的速度运动到点 P，再沿线段 PD 以每秒 2 个单位的速度运动到点 D 后停止，求点 H 在整个运动过程中所用时间最少时点 P 的坐标．
答案
第一部分
1. D【解析】−2<0<14<2，即最大的是 2．
2. C【解析】A、 12+22=32，符合勾股定理的逆定理，故本选项不符合题意；
B、 72+242=252，符合勾股定理的逆定理，故本选项不符合题意；
C、 42+52≠62，不符合勾股定理的逆定理，故本选项符合题意；
D、 352+452=12，符合勾股定理的逆定理，故本选项不符合题意．
故选：C．
3. A【解析】如图，
因为 ∠1=115∘，∠2=115∘，
所以 ∠1=∠2，
所以 a∥b，
所以 ∠4=∠5，
因为 ∠3=124∘，
所以 ∠4=∠5=180∘−∠3=56∘．
4. C
5. B
【解析】根据题意知，点 M 原来的坐标为 −1+3,2，即 2,2．
6. B
7. D【解析】y=2x−4, ⋯⋯①3x+y=1. ⋯⋯②
把①代入②得：3x+2x−4=1，解得：x=1，
把 x=1 代入①得：y=−2，则 1,−2 位于第四象限．
8. C【解析】A、 49 的平方根是 ±7，是真命题，不符合题意；
B、点 M1,a 和点 N3,b 是一次函数 y=−2x+1 图象上的两点，则 a=−1，b=−5，a>b，是真命题，不符合题意；
C、无限小数都是无理数，是假命题，符合题意；
D、点 −2,3 到 y 轴的距离是 2，是真命题，不符合题意．
9. D【解析】因为 k<0，
所以 −k>0，
所以一次函数 y=kx−k 的图象经过第一、二、四象限．
10. B
【解析】设当 4≤x≤6 时，y 与 x 的函数关系式为 y=kx+b．
4k+b=240,10k+b=0, 得 k=−40,b=400,
即当 4≤x≤6 时，y 与 x 的函数关系式为 y=−40x+400，
当 x=6 时，y=−40×6+400=160，
即小明出发 6 小时后距A地 160 千米．
11. B
12. B【解析】如图所示：
∵ 在 Rt△ABC 中，∠C=90∘，AC=8 cm，BC=6 cm，
∴AB=AC2+BC2=10 cm
∵EDʹ 是 AB 的中垂线，
∴BE=5，
连接 BDʹ，
∴BDʹ=ADʹ，
在 Rt△CBDʹ 中，BDʹ2=CDʹ2+BC2，
即 ADʹ2=62+8−ADʹ2，解得：ADʹ=254，
∴ 当点 D 运动到线段 AB 的中垂线上时，运动时间为 254 秒．
第二部分
13. 0,4
【解析】∵ 点 Ma−3,a+1 在 y 轴上，
∴a−3=0，
解得：a=3，
所以，a+1=4，
所以，点 M 的坐标为 0,4．
故答案为：0,4．
14. x=2,y=4
【解析】∵y=x+2 的图象经过 Pm,4，
∴4=m+2，
∴m=2，
∴ 一次函数 y=kx+b 与 y=x+2 的图象相交于点 P2,4，
∴ 方程组 y=x+2,y=kx+b 的解是 x=2,y=4.
15. 1.6
【解析】这组数据的平均数是：5+3+3+6+3÷5=4，
则这组数据的方差是 S2=155−42+3×3−42+6−42=1.6．
16. 5,−6
【解析】如图所示，将线段 AB 绕点 B 顺时针旋转 90∘ 得到线段 BC，
则点 C 的坐标为 −4,−8，
由于旋转可知，△ABC 为等腰直角三角形，
令线段 AC 和线段 BP 交于点 M，则 M 为线段 AC 的中点，
∴ 点 M 的坐标为 4,−4，又 B 为 0,4，
设直线 BP 为 y=kx+b，将点 B 和点 M 代入可得 4k+b=−4,b=4,
解得 k=−2，b=4，可得直线 BP 为 y=−2x+4，
由于点 P 为直线 BP 和直线 y=−x−1 的交点，
则由 y=−2x+4,y=−x−1 解得 x=5,y=−6,
∴ 点 P 的坐标为 5,−6．
第三部分
17. （1） 原式=32−22−2=2−2.
（2） 原式=23+26×3−12×22=6+62−62=6.
18.
2x−3y=5, ⋯⋯①3x+y=2. ⋯⋯②
由②得
y=2−3x. ⋯⋯③
把③代入①，得
2x−32−3x=5.2x−6+9x=5.11x=11.x=1.
把 x=1 代入③中得
y=2−3×1=−1.
该方程组的解是
x=1,y=−1.
19. （1） 20
【解析】1+1+3+4+6+2+2+1=20．
（2） 4；4
【解析】众数是 4，中位数是 4．
（3） 每个人读书本数的平均数是：
x=120×1+2×1+3×3+4×6+5×4+6×2+7×2+8=4.5.
∴ 总数是：800×4.5=3600．
答：估计该校学生这学期读书总数约为 3600 本．
20. ∵∠AEF=∠F，
∴PF∥AD，
∴∠ADC=∠CPF，
又 ∵∠BAD=∠CPF，
∴∠BAD=∠ADC，
∴AB∥CD，
∴∠ABD+∠BDC=180∘．
21. （1） 设购进猕猴桃 x 千克，购进芒果 y 千克，
根据题意得：
x+y=50,20x+40y=1600.
解得：
x=20,y=30.
答：购进猕猴桃 20 千克，购进芒果 30 千克．
（2） 26×20+50×30−1600=420（元）．
答：如果猕猴桃和芒果全部卖完，他能赚 420 元钱．
22. （1） 画图如下：
4
【解析】如图所示：△ABC 的面积是：3×4−12×1×2−12×2×4−12×2×3=4．
（2） −4,3
（3） ∵P 为 x 轴上一点，△ABP 的面积为 4，
∴BP=8，
∴ 点 P 的横坐标为：2+8=10 或 2−8=−6，
故 P 点坐标为：10,0 或 −6,0．
23. （1） −2,0；0,2
【解析】直线 l2：y=x+2，令 y=0，则 x=−2，令 y=0，则 x=2．
（2） y=2x−2
【解析】y=2x+1 向下平移 3 个单位长度得到直线 l1，则直线 l1 的表达式为：y=2x−2．
（3） ∵S△AOE=2S△ABO，
∴yE=2OB=4，
将 yE=4 代入 l1 的表达式得：4=2x−2，解得：x=3，
将 yE=−4 代入 l1 的表达式得：−4=2x−2，解得：x=−1，
则点 E 的坐标为 3,4 或 −1,−4．
（4） 过点 P，C 分别作 y 轴的平行线，分别交过点 D 作 x 轴平行线于点 H，Hʹ，HʹC 交 BD 于点 Pʹ，
直线 l2：y=x+2，则 ∠ABO=45∘=∠HBD，PH=122PD，
点 H 在整个运动过程中所用时间 =PC1+PD2=PH+PC，
当 C，P，H 在一条直线上时，PH+PC 最小，即为 CHʹ=6，点 P 坐标 1,3，
故：点 H 在整个运动过程中所用最少时间为 6 秒，此时点 P 的坐标 1,3．