2018-2019学年广东深圳福田区深圳实验学校初中部七上期末数学试卷

这是一份2018-2019学年广东深圳福田区深圳实验学校初中部七上期末数学试卷，共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共12小题；共60分）
1. 在 2，12，−8，−2，0 中，互为相反数的是
A. 0 与 2B. 12 与 −2C. 2 与 −2D. 0 与 −8

2. 在 x2y，15，−8x+4y，43ab 四个代数式中，单项式有
A. 1 个B. 2 个C. 3 个D. 4 个

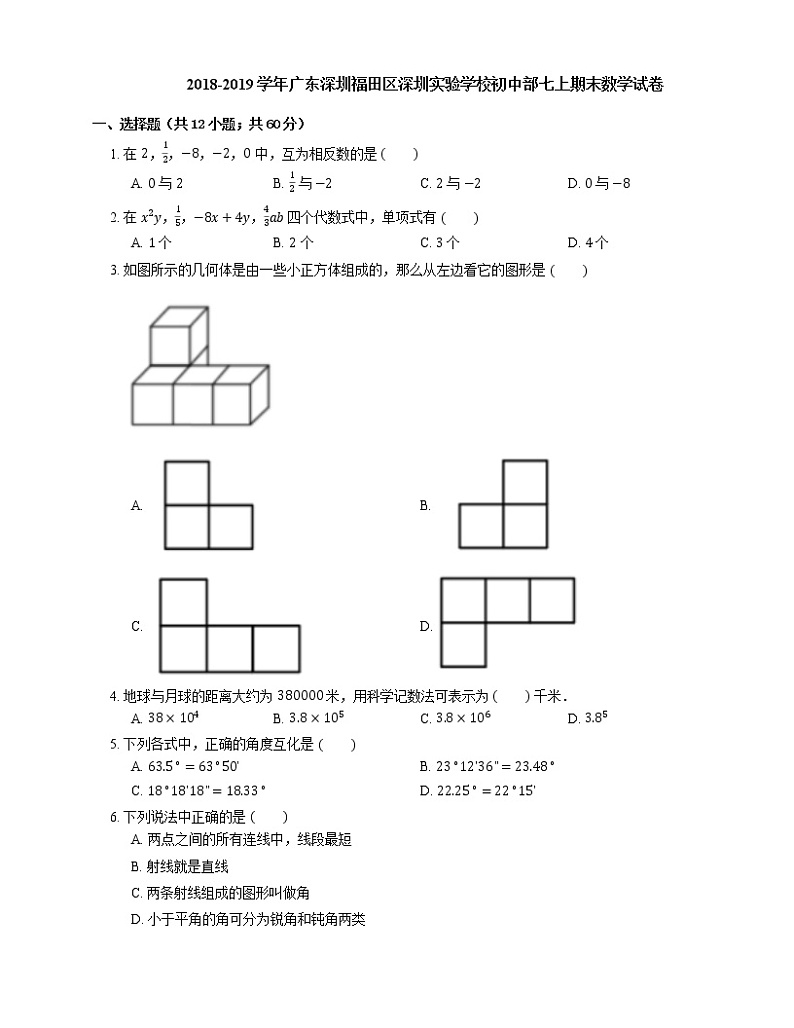
3. 如图所示的几何体是由一些小正方体组成的，那么从左边看它的图形是
A. B.
C. D.

4. 地球与月球的距离大约为 380000 米，用科学记数法可表示为 千米．
A. 38×104B. 3.8×105C. 3.8×106D. 3.85

5. 下列各式中，正确的角度互化是
A. 63.5∘=63∘50ʹB. 23∘12ʹ36ʺ=23.48∘
C. 18∘18ʹ18ʺ=18.33∘D. 22.25∘=22∘15ʹ

6. 下列说法中正确的是
A. 两点之间的所有连线中，线段最短
B. 射线就是直线
C. 两条射线组成的图形叫做角
D. 小于平角的角可分为锐角和钝角两类

7. 如图所示，有理数 a，b 在数轴上的位置，化简 ∣1+a∣+∣1−b∣ 的值为 ．
A. a+bB. a+b−2C. −a−bD. a−b+2

8. 如果关于 x 的方程 3x−5m=3 与方程 2x+10=2 的解相同，那么 m=
A. −2B. −3C. 3D. 1

9. 直线 a 上有 5 个不同的点 A，B，C，D，E，则该直线上共有 条线段．
A. 8B. 9C. 12D. 10

10. 点 C 在线段 AB 上，下列条件中不能确定点 C 是线段 AB 中点的是
A. AC=BCB. AC+BC=ABC. AB=2ACD. BC=12AB

11. 一款新型的太阳能热水器进价 2000 元，标价 3000 元，若商场要求以利润率不低于 5% 的售价打折出售，则设销售员出售此商品最低可打 x 折，由题意列方程，得
A. 3000x=20001−5%B. 3000x−20002000=5%
C. 3000⋅x10=2000⋅1−5%D. 3000⋅x10=2000⋅1+5%

12. 若 x 是不等于 1 的实数，我们把 11−x 称为 x 的差倒数，如 2 的差倒数是 11−2=−1，−1 的差倒数为 11−−1=12，现已知 x1=−13，x2 是 x1 的差倒数，x3 是 x2 的差倒数，x4 是 x3 的差倒数，⋯，依此类推，则 x2019 的值为
A. −13B. −1C. 34D. 4

二、填空题（共4小题；共20分）
13. 代数式 −32xy 的系数是 ．

14. 若 m2−2m=1，则 2m2−4m+2017 的值是 ．

15. 如果方程 m−1x∣m∣+2=0 是表示关于 x 的一元一次方程，那么 m 的取值是 ．

16. 下面每个表格中的四个数都是按相同规律填写的：
132726426396574128100⋯a21bx第 1 个第 2 个第 3 个第 4 个

三、解答题（共7小题；共91分）
17. 完成下列各题．
（1）计算：
① 22×−12+∣−4∣+−2．
② −22×15−−52÷5−5．
（2）解方程：
① 2x+18=−3x−2．
② 2x−35−2x+110=1．

18. 先化简，再求值：2a2−ab−3a2−ab，其中，a=−2，b=3．

19. 已知：A−2B=7a2−7ab，且 B=−4a2+6ab+7．
（1）求 A 等于多少?
（2）若 3x2ayb+1 与 −12x2ya+3 是同类项，求 A 的值．

20. 某文艺团体为“希望工程”募捐组织了一场义演，共售出 2000 张票，筹得票款 13600 元．已知学生票 5 元/张，成人票 8 元/张，问成人票与学生票各售出多少张?

21. 某校八年级学生全部参加“初二生物地理会考”，从中抽取了部分学生的生物考试成绩，将他们的成绩进行统计后分为 A，B，C，D四个等级，并将统计结果绘制成如下的统计图，请结合图中所给的信息解答下列问题：
（1）抽取了 名学生成绩．
（2）请把频数分布直方图补充完整．
（3）扇形统计图中 A等级所在的扇形的圆心角度数是 ．
（4）若 A，B，C 三个等级为合格，该校初二年级有 900 名学生，估计全年级生物合格的学生人数．

22. 如图，∠AOB 是平角，∠DOE=90∘，OC 平分 ∠DOB．
（1）若 ∠AOE=32∘，求 ∠BOC 的度数．
（2）若 OD 是 ∠AOC 的角平分线，求 ∠AOE 的度数．

23. 已知 a 是最大的负整数，b，c 满足 b−32+∣c+4∣=0，且 a，b，c 分别是点 A，B，C 在数轴上对应的数．
（1）点 A 表示的数为 ，点 B 表示的数为 ，点 C 表示的数为 ．
（2）若动点 P 从 C 出发沿数轴正方向运动，点 P 的速度是每秒 2 个单位长度，运动几秒后，点 P 到点 B 为 5 个单位长度?
（3）在数轴上找一点 M，使点 M 到 A，B，C 三点的距离之和等于 13，请写出所有点 M 对应的数，并写出求解过程．
答案
第一部分
1. C【解析】2 与 −2 互为相反数．
2. C【解析】在 x2y，15，−8x+4y，43ab 四个代数式中，单项式有 x2y，15，43ab 共 3 个．
3. A【解析】左视图为物体的左侧看过去的图形，所以应该选择A选项．
4. B【解析】380000=3.8×105
5. D
【解析】A：63.5∘=63∘30ʹ．
B：23∘12ʹ36ʺ=23.21∘．
C：18∘18ʹ18ʺ=18.305∘．
6. A【解析】A，两点之间的所有连线中，线段最短，选项正确；
B，射线是直线的一部分，选项错误；
C，有公共端点的两条射线组成的图形叫做角，选项错误；
D，小于平角的角可分为锐角，钝角，还应包含直角，选项错误．
7. A【解析】由图可知：−1 原式=∣1+a∣+∣1−b∣=1+a+b−1=a+b.
8. B【解析】方程 2x+10=2 的解为 x=−4，
∵ 方程 3x−5m=3 与方程 2x+10=2 的解相同，
∴ 方程 3x−5m=3 的解为 x=−4，
当 x=−4 时，−12−5m=3，
解得 m=−3．
9. D【解析】根据题意画图：
由图可知有 AB，AC，AD，AE，BC，BD，BE，CD，CE，DE，共 10 条．
10. B
11. D【解析】设销售员出售此商品最低可打 x 折，
根据题意得：3000⋅x10=20001+5%．
12. D【解析】由已知可得，x1=−13，x2=11−−13=34，x3=11−34=4，x4=11−4=−13，
可知每三个一个循环，2019÷3=673，故 x2019=4．
第二部分
13. −32
【解析】代数式 −32xy 的系数是：−32．
14. 2019
【解析】当 m2−2m=1 时，
2m2−4m+2017=2m2−2m+2017=2×1+2017=2+2017=2019.
15. −1
【解析】m−1x∣m∣+2=0 是关于 x 的一元一次方程，
∴∣m∣=1m−1≠0，
∴m=±1m≠1，
∴m=−1．
16. 301
【解析】观察可知：3a=21，解得：a=7，
∴b=14，
∴x=21×14+7=301．
第三部分
17. （1） ①
原式=4×−12+4−2=−2+4−2=0.
②
原式=4×15−25÷5−5=60−5−5=50.
（2） ①
2x+18=−3x−2,2x+3x=−2−18,5x=−20,x=−4.
②
2x−35−2x+110=1,22x−3−2x+1=10,4x−6−2x−1=10,4x−2x=10+6+1,2x=17,x=172.
18. 原式=2a2−2ab−3a2+3ab=−a2+ab，
当 a=−2，b=3 时，
原式=−−22+−2×3=−4−6=−10.
19. （1） ∵B=−4a2+6ab+7，
∴A=2B+7a2−7ab=2−4a2+6ab+7+7a2−7ab=−8a2+12ab+14+7a2−7ab=−a2+5ab+14.
（2） 由题意可知：2a=2，b+1=a+3，
即 a=1，b=3，
当 a=1，b=3 时，
原式=−1+5×1×3+14=28.
20. 设成人票售出 x 张，则学生票售出 2000−x 张，根据题意可得：8x+52000−x=13600，
解得：x=1200，
2000−x=2000−1200=800（张），
答：成人票售出 1200 张，学生票售出 800 张．
21. （1） 50
【解析】抽取的学生总数为：23÷46%=50（名）．
（2） D等级的学生有 50−10+23+12=5（名），补全频数分布直方图，如图所示：
（3） 72∘
【解析】A等级所在的扇形的圆心角度数 =1050×360∘=72∘．
（4） 根据题意得：9001−550=810（人）．
答：全年级生物合格的学生共约 810 人．
22. （1） ∠AOD=∠DOE−∠AOE=90∘−32∘=58∘，
∠BOD=∠AOB−∠AOD=180∘−58∘=122∘，
又 OC 平分 ∠BOD，
∴∠BOC=12∠BOD=12×122∘=61∘．
（2） ∵OC 平分 ∠BOD，OD 平分 ∠AOC，
∴∠BOC=∠DOC=∠AOD，
又 ∠BOC+∠DOC+∠AOD=180∘，
∴∠AOD=13×180∘=60∘，
∴∠AOE=∠DOE−∠AOD=90∘−60∘=30∘．
23. （1） −1；3；−4
【解析】∵a 是最大的负整数，
∴a=−1，
∵b−32≥0，∣c+4∣≥0，而 b−32+∣c+4∣=0，
∴b=3，c=−4．
故答案为：−1；3；−4．
（2） 设点 P 运动 t 秒时到点 B 为 5 个单位长度，分以下两种情况：
①点 P 在点 B 左边距离点 B5 个单位，则有：
2t+5=3−−4，
解得 t=1，
②点 P 在点 B 右边距离点 B5 个单位，则有：
2t−5=3−−4，
解得 t=6，
故当点 P 运动 1 秒或 6 秒后，点 P 到点 B 为 5 个单位长度．
（3） 点 B 与点 C 之间的任何一点时到 A，B，C 三点的距离之和都小于 13，
因此点 M 的位置只有以下两种情况，设点 M 所表示的数为 m，则：
①点 M 在点 C 左边时，可得：
−4−m−1−m+3−m=13，
解得 m=−5，
②点 M 在点 B 右边时，可得：
m+4+m+1+m−3=13，
解得 m=113，
故点 M 对应的数为 −5 或 113．