2018_2019学年广东省深圳市龙华区八上期末数学试卷

这是一份2018_2019学年广东省深圳市龙华区八上期末数学试卷，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共12小题；共60分）
1. 4 的算术平方根是
A. ±2B. 2C. −2D. ±16

2. 如图，已知 a∥b，∠1=75∘，则 ∠2 的度数是
A. 35∘B. 75∘C. 105∘D. 125∘

3. 下列各组数中，能作为直角三角形的三边长的是
A. 1，2，3B. 2，3，5C. 3，3，5D. 6，8，9

4. 下列各组数值是二元一次方程 2x−y=4 的解的是
A. x=3,y=2B. x=1,y=−1C. x=0,y=4D. x=0.5,y=3

5. 下列二次根式是最简二次根式的是
A. 12B. 8C. 10D. 16

6. 小明在八年级上学期期中测试中各学科得分如表：
单元语文数学英语物理历史生物地理分数85809280859585
则下列判断正确的是
A. 平均数是 85B. 众数是 85C. 中位数是 80D. 方差是 85

7. 初三（1）班的座位表如图所示，如果如图所示建立平面直角坐标系，并且“过道也占一个位置”，例如小王所对应的坐标为 3,2，小芳的为 5,1，小明的为 10,2，那么小李所对应的坐标是
A. 6,3B. 6,4C. 7,4D. 8,4

8. 如图，在数轴上，点 A 表示实数 3，AB=2，连接 OB，以 O 为圆心，OB 为半径作弧，交数轴于点 C，则点 C 表示的实数是
A. −4B. 3.5C. 10D. 13

9. 下列命题中，是真命题的是
A. 两直线平行，同旁内角相等
B. 三角形的一个外角等于两个内角的和
C. 9 是无理数
D. 平面直角坐标系内，点 A2,−3 关于 x 轴对称的点的坐标是 2,3

10. 放学后，小刚和同学边聊边往家走，突然想起今天是妈妈的生日，赶紧加快速度，跑步回家．小刚离家的距离 s（单位 m）和放学后的时间 t（单位 min）之间的关系如图所示，那么下列说法错误的是
A. 小刚边走边聊阶段的行走速度是 125 m/min
B. 小刚家离学校的距离是 1000 m
C. 小刚回到家时已放学 10 min
D. 小刚从学校回到家的平均速度是 100 m/min

11. 对于一次函数 y=kx−kk≠0，下列说法中正确的是
A. 当 k>0 时，该函数图象不经过第三象限
B. 函数值 y 随自变量 x 值的增大而增大
C. 当 k=2 时，该函数的图象与坐标轴围成的三角形的面积为 2
D. 该函数的图象一定经过点 1,0

12. 《九章算术》是我国古代第一部数学专著，其中有这样一道名题：“今有善行者行一百步，不善行者行六十步，今不善行者先行一百步，善行者追之，问几步及之?”意思是说：走路快的人走 100 步的时候，走路慢的才走了 60 步，走路慢的人先走 100 步，然后走路快的人去追赶，问走路快的人要走多少步才能追上?若设走路快的人要走 x 步才能追上走路慢的人，此时走路慢的人又走了 y 步，根据题意可列方程组为
A. x100=y60,x−y=100B. x60=y100,x−y=100C. x100=y60,x+y=100D. x60=y100,x+y=100

二、填空题（共4小题；共20分）
13. 比较大小：6 3（填：“>”或“<”或“=”）．

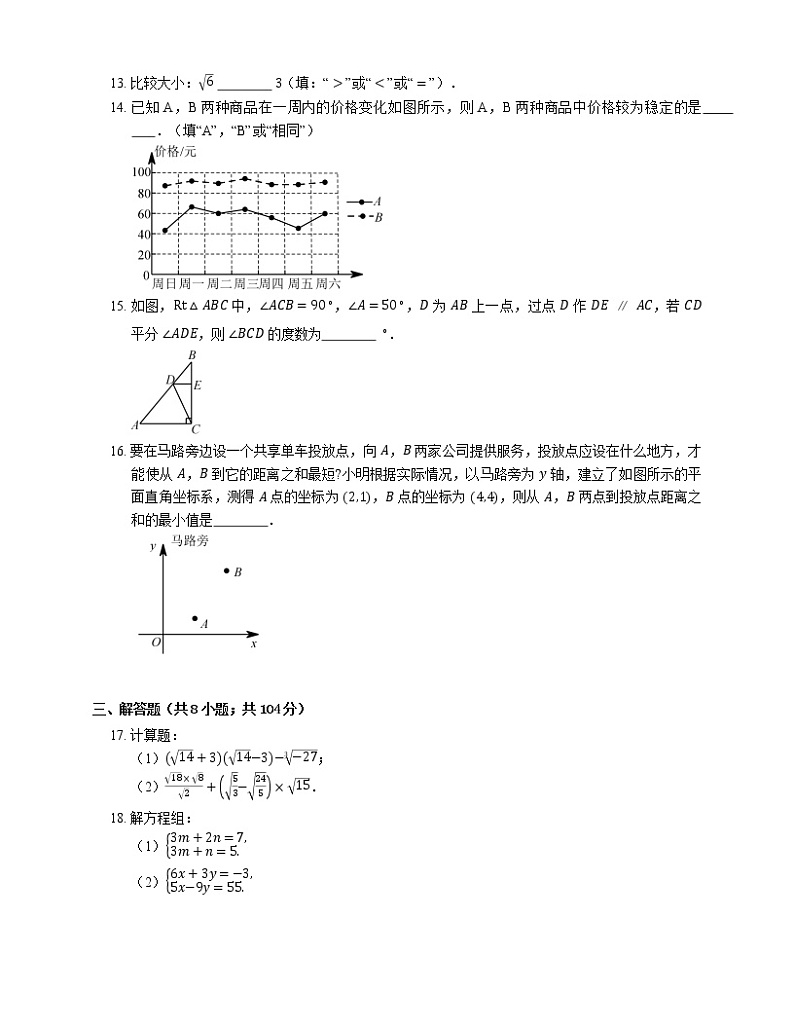
14. 已知A，B两种商品在一周内的价格变化如图所示，则A，B两种商品中价格较为稳定的是 ．（填“A”，“B”或“相同”）

15. 如图，Rt△ABC 中，∠ACB=90∘，∠A=50∘，D 为 AB 上一点，过点 D 作 DE∥AC，若 CD 平分 ∠ADE，则 ∠BCD 的度数为 ∘．

16. 要在马路旁边设一个共享单车投放点，向 A，B 两家公司提供服务，投放点应设在什么地方，才能使从 A，B 到它的距离之和最短?小明根据实际情况，以马路旁为 y 轴，建立了如图所示的平面直角坐标系，测得 A 点的坐标为 2,1，B 点的坐标为 4,4，则从 A，B 两点到投放点距离之和的最小值是 ．

三、解答题（共8小题；共104分）
17. 计算题：
（1）14+314−3−3−27；
（2）18×82+53−245×15．

18. 解方程组：
（1）3m+2n=7,3m+n=5.
（2）6x+3y=−3,5x−9y=55.

19. 随着新学校建成越来越多，绝大部分孩子已能就近入学，某数学学习兴趣小组对八年级（1）班学生上学的交通方式进行问卷调查，并将调查结果画出下列两个不完整的统计图（图 1 、图 2）．请根据图中的信息完成下列问题．
（1）该班参与本次问卷调查的学生共有 人；
（2）请补全图 1 中的条形统计图；
（3）在图 2 的扇形统计图中，“骑车”所在扇形的圆心角的度数是 度．

20. 如图，已知直线 l1∥l2∥l3，Rt△ABC 的直角顶点 C 在直线 l1 上，点 B 在直线 l2 上，点 A 在直线 l3 上，l2 与 AC 交于点 D，且 ∠BAC=25∘，∠BAE=25∘．
（1）求证：△ABD 是等腰三角形；
（2）求 ∠BCF 的度数．

21. 已知函数 y=2x−2 的图象如图所示．
（1）请在图所示的平面直角坐标系内，按画函数图象的基本步骤画出函数 y=12x+1 的图象；
（2）根据图象得方程组 y=2x−2,y=12x+1 的解是 ．

22. 已知甲、乙两家公司在销售某种品牌的新能源汽车时销售利润（万元）与销售量（台）之间的关系如图所示，射线 l1 反映的是甲公司销售利润与销售量的关系，折线 l2 反映的是乙公司销售利润与销售量的关系．
（1）甲公司每销售一台这种品牌汽车可获利 万元；如果乙公司没有售出这种品牌汽车，则该公司将亏损 万元；
（2）当乙公司销售量不少于 20 台时，求该公司的销售利润与销售量之间的函数关系式．

23. 某水果店购进苹果与橙子共 50 kg 机型销售，这两种水果的进价、标价如表所示，店主将这些水果按 8 折全部售出后，其获利 258 元，那么该水果点购进苹果和橙子分别多少 kg?
进价元/kg标价元/kg苹果615橙子512

24. 如图 1，已知函数 y=12x+3 与 x 轴交于点 A，与 y 轴交于点 B，点 C 与点 A 关于 y 轴对称．
（1）求直线 BC 的函数解析式；
（2）设点 M 是 x 轴上的一个动点，过点 M 作 y 轴的平行线，交直线 AB 于点 P，交直线 BC 于点 Q．
①若 △PQB 的面积为 94，求点 M 的坐标；
②连接 BM，如图 2，若 ∠BMP=∠BAC，求点 P 的坐标．
答案
第一部分
1. B【解析】∵22=4，
∴4 的算术平方根是 2．
2. C【解析】∵ 直线 l 直线 a，b 相交，且 a∥b，∠1=75∘，
∴∠3=∠1=75∘，
∴∠2=180∘−∠3=180∘−75∘=105∘．
3. B
4. A
5. C
6. B【解析】A、由平均数公式求得这组数据的平均数是 86，故选项错误；
B、这组数据中 85 出现了 3 次，出现的次数最多，所以这组数据的众数位 85，故此选项正确；
C、按照从小到大排列，正中间的数是 85，即中位数是 85，故选项错误；
D、 s2=17×3×86−852+2×86−802+92−862+95−862≈27.43，故方差大约是 27.43，故此选项错误．
7. C
8. D【解析】根据题意得：OC=OB=32+22=13．
9. D【解析】两直线平行，同旁内角互补，A是假命题；
三角形的一个外角等于与它不相邻的两个内角的和，B是假命题；
9=3 是有理数，C是假命题；
平面直角坐标系内，点 A2,−3 关于 x 轴对称的点的坐标是 2,3，D是真命题．
10. A
11. D【解析】A．当 k>0 时，−k<0，函数图象经过第一、三、四象限，故本选项错误；
B．当 k>0 时，y 随 x 的增大而增大，当 k<0 时，y 随 x 的增大而减小，故本选项错误；
C．当 k=2 时，则 y=2x−2，函数图象与 x 轴的交点为 1,0，与 y 轴的交点 0,−2，
所以函数的图象与坐标轴围成的三角形的面积 =12×2×1=1，故本选项错误；
D．把 x=1 代入 y=kx−k 得 y=k−k=0，则函数图象一定经过点 1,0，故本选项正确．
12. A【解析】设走路快的人要走 x 步才能追上走路慢的人，此时走路慢的人又走了 y 步，
根据题意，得 x100=y60,x−y=100.
第二部分
13. <
【解析】∵6<9，
∴6<3．
14. B
【解析】由图可知，B的商品中价格较为稳定，数据波动小．
15. 25
【解析】∵DE∥AC，CD 平分 ∠ADE，
∴∠ACD=∠CDE=∠CDA，
∴AD=AC，
又 ∵∠A=50∘，
∴∠ACD=65∘，
又 ∵∠ACB=90∘，
∴∠BCD=90∘−65∘=25∘．
16. 35
【解析】作 A 关于 y 轴的对称点 C，
则 C 的坐标是 −2,1．
设 BC 的解析式是 y=kx+b，
则 4k+b=4,−2k+b=1,
解得：k=12,b=2,
则 BC 的解析式是 y=12x+2．
令 x=0，解得：y=2，
则派送点的坐标是 0,2．
从 A，B 两点到投放点距离之和的最小值是 62+4−12=35．
第三部分
17. （1） 原式=142−32−−3=14−9+3=8.
（2） 原式=18×4+53×15−245×15=62+5−62=5.
18. （1）
3m+2n=7, ⋯⋯①3m+n=5. ⋯⋯②①−②
得：
n=2.
把 n=2 代入 ① 得：
3m+2×2=7.
所以
m=1.
所以原方程组的解为
m=1,n=2.
（2）
6x+3y=−3, ⋯⋯①5x−9y=55. ⋯⋯②①×3+②
得：
23x=46.
所以
x=2.
把 x=2 代入 ① 得：
12+3y=−3.
所以
y=−5.
所以原方程组的解为
x=2,y=−5.
19. （1） 50．
（2）
（3） 129.6
20. （1） ∵l2∥l3，
∴∠ABD=∠BAE=25∘，
∵∠BAC=25∘，
∴∠ABD=∠BAC，
∴△ABD 是等腰三角形．
（2） ∵∠BAC+∠ACB+∠ABC=180∘，∠BAC=25∘，∠ACB=90∘，
∴∠ABC=180∘−∠BAC−∠ACB=180∘−25∘−90∘=65∘，
∴∠CBD=∠ABC−∠ABD=65∘−25∘=40∘，
∵l1∥l2，
∴∠BCF=∠CBD=40∘．
21. （1） 列表得：
x0−2y10
描点；连线（图象如图所示）：
（2） x=2,y=2
22. （1） 0.75；5
（2） 设当乙公司销售量超过 20 台时，求该公司的销售利润与销售量之间的函数关系式为 y=kx+b，
由图象得 20k+b=5,40k+b=30,
解得：k=54,b=−20.
∴y=54x−20（其中 x>20）．
23. 设苹果购进了 x 千克，则橙子购进了 y 千克，
根据题意可得：
x+y=50,15×0.8x+12×0.8y=258+6x+5y,
解得：
x=20,y=30.
答：该水果点购进苹果和橙子分别 20 kg，30 kg．
24. （1） 对于 y=12x+3，由 x=0 得：y=3，
∴B0,3，
由 y=0 得：12x+3=0，解得 x=−6，
∴A−6,0，
∵ 点 C 与点 A 关于 y 轴对称，
∴C6,0，
设直线 BC 的函数解析式为 y=kx+b，
b=3,6k+b=0, 解得 k=−12,b=3,
∴ 直线 BC 的函数解析式为 y=−12x+3．
（2） ①设 Mm,0，则 Pm,12m+3，Qm,−12m+3，
如图 1，过点 B 作 BD⊥PQ 于点 D，
∴PQ=−12m+3−12m+3=m，BD=m，
∴S△PQB=12PQ⋅BD=12m2=94，解得 m=±322，
∴M322,0 或 M−322,0．
②如图 3，当点 M 在 y 轴的左侧时，
∵ 点 C 与点 A 关于 y 轴对称，
∴AB=BC，
∴∠BAC=∠BCA，
∵∠BMP=∠BAC，
∴∠BMP=∠BCA，
∵∠BMP+∠BMC=90∘，
∴∠BMC+∠BCA=90∘，
∴∠MBC=180∘−∠BMC+∠BCA=90∘，
∴BM2+BC2=MC2，
设 Mx,0，则 Px,12x+3，
∴BM2=OM2+OB2=x2+9，MC2=6−x2，BC2=OC2+OB2=62+32=45，
∴x2+9+45=6−x2，解得 x=−32，
∴P−32,94；
当点 M 在 y 轴的右侧时，如图 2，
同理可得 P32,154．
综上，点 P 的坐标为 −32,94 或 32,154．
【解析】②如图 3，当点 M 在 y 轴的左侧时，
∵ 点 C 与点 A 关于 y 轴对称，
∴AB=BC，
∴∠BAC=∠BCA，
∵∠BMP=∠BAC，
∴∠BMP=∠BCA，
∵∠BMP+∠BMC=90∘，
∴∠BMC+∠BCA=90∘，
∴∠MBC=180∘−∠BMC+∠BCA=90∘，
设直线 BM 为 y=k1x+b1，则有 k1×−12=−1，
∴k1=2，
∴ 直线 BM 为 y=2x+b1，将点 B0,3 代入得，b1=3，
∴ 直线 BM 为 y=2x+3，由 y=0 得 x=−32，
将 x=−32 代入 y=12x+3 得 y=94，
∴P−32,94；
当点 M 在 y 轴的右侧时，如图 2，同理可得 P32,154．
综上，点 P 的坐标为 −32,94 或 32,154．