2021学年第23章 图形的相似23.3 相似三角形3. 相似三角形的性质课堂检测
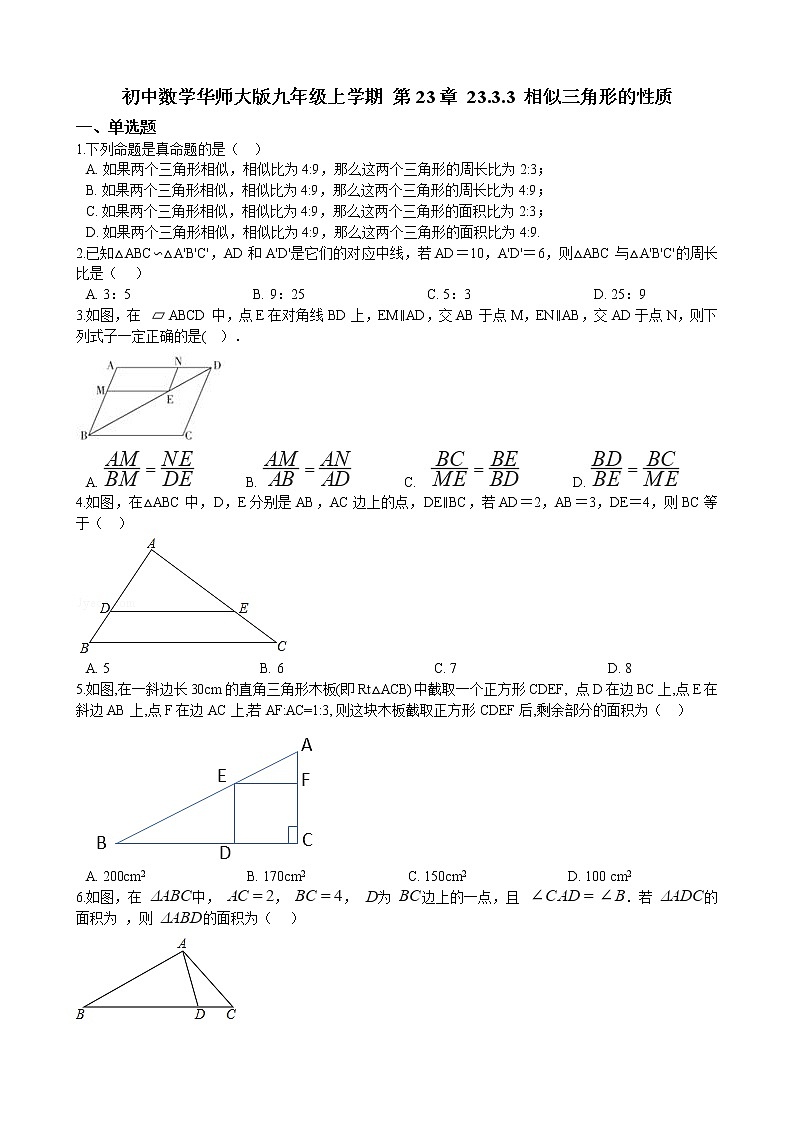
展开1.下列命题是真命题的是( )
A. 如果两个三角形相似,相似比为4:9,那么这两个三角形的周长比为2:3;
B. 如果两个三角形相似,相似比为4:9,那么这两个三角形的周长比为4:9;
C. 如果两个三角形相似,相似比为4:9,那么这两个三角形的面积比为2:3;
D. 如果两个三角形相似,相似比为4:9,那么这两个三角形的面积比为4:9.
2.已知△ABC∽△A'B'C',AD和A'D'是它们的对应中线,若AD=10,A'D'=6,则△ABC与△A'B'C'的周长比是( )
A. 3:5 B. 9:25 C. 5:3 D. 25:9
3.如图,在 ABCD中,点E在对角线BD上,EM∥AD,交AB于点M,EN∥AB,交AD于点N,则下列式子一定正确的是( ).
A. B. C. D.
4.如图,在△ABC中,D,E分别是AB,AC边上的点,DE∥BC,若AD=2,AB=3,DE=4,则BC等于( )
A. 5 B. 6 C. 7 D. 8
5.如图,在一斜边长30cm的直角三角形木板(即Rt△ACB)中截取一个正方形CDEF, 点D在边BC上,点E在斜边AB上,点F在边AC上,若AF:AC=1:3,则这块木板截取正方形CDEF后,剩余部分的面积为( )
A. 200cm2 B. 170cm2 C. 150cm2 D. 100 cm2
6.如图,在 中, , , 为 边上的一点,且 .若 的面积为 ,则 的面积为( )
A. B. C. D.
二、填空题
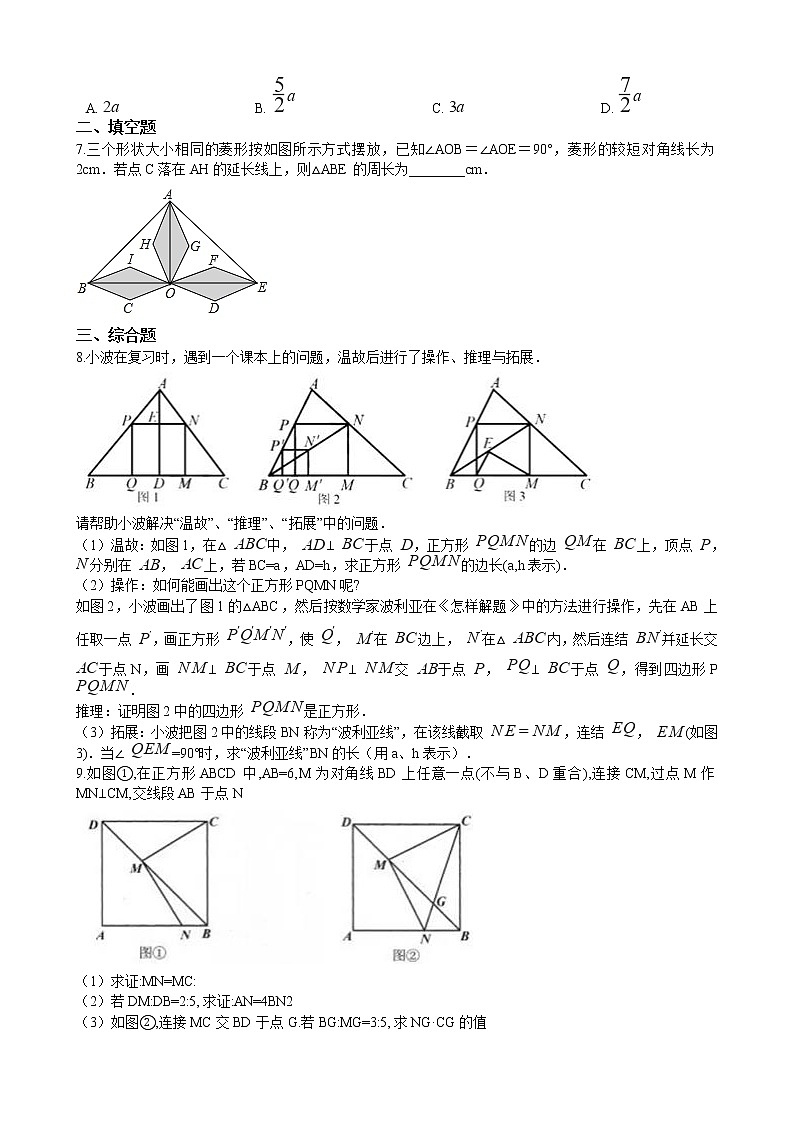
7.三个形状大小相同的菱形按如图所示方式摆放,已知∠AOB=∠AOE=90°,菱形的较短对角线长为2cm.若点C落在AH的延长线上,则△ABE的周长为________cm.
三、综合题
8.小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.
请帮助小波解决“温故”、“推理”、“拓展”中的问题.
(1)温故:如图1,在△ 中, ⊥ 于点 ,正方形 的边 在 上,顶点 , 分别在 , 上,若 BC=a,AD=h,求正方形 的边长(a,h表示).
(2)操作:如何能画出这个正方形PQMN呢?
如图2,小波画出了图1的△ABC,然后按数学家波利亚在《怎样解题》中的方法进行操作,先在AB上任取一点 ,画正方形 ,使 , 在 边上, 在△ 内,然后连结 并延长交 于点N,画 ⊥ 于点 , ⊥ 交 于点 , ⊥ 于点 ,得到四边形P .
推理:证明图2中的四边形 是正方形.
(3)拓展:小波把图2中的线段BN称为“波利亚线”,在该线截取 ,连结 , (如图3).当∠ =90°时,求“波利亚线”BN的长(用a、h表示).
9.如图①,在正方形ABCD中,AB=6,M为对角线BD上任意一点(不与B、D重合),连接CM,过点M作MN⊥CM,交线段AB于点N
(1)求证:MN=MC:
(2)若DM:DB=2:5,求证:AN=4BN2
(3)如图②,连接MC交BD于点G.若BG:MG=3:5,求NG·CG的值
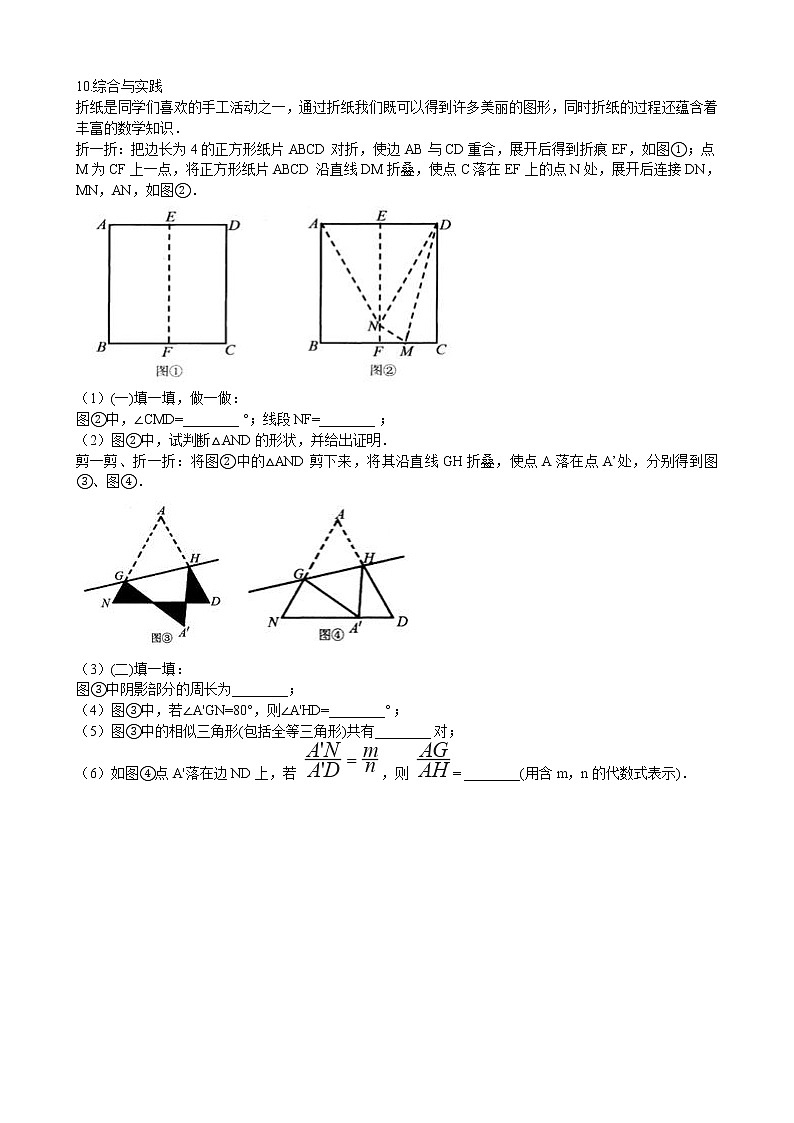
10.综合与实践
折纸是同学们喜欢的手工活动之一,通过折纸我们既可以得到许多美丽的图形,同时折纸的过程还蕴含着丰富的数学知识.
折一折:把边长为4的正方形纸片ABCD对折,使边AB与CD重合,展开后得到折痕EF,如图①;点M为CF上一点,将正方形纸片ABCD沿直线DM折叠,使点C落在EF上的点N处,展开后连接DN,MN,AN,如图②.
(1)(一)填一填,做一做:
图②中,∠CMD=________ °;线段NF=________ ;
(2)图②中,试判断△AND的形状,并给出证明.
剪一剪、折一折:将图②中的△AND剪下来,将其沿直线GH折叠,使点A落在点A’处,分别得到图③、图④.
(3)(二)填一填:
图③中阴影部分的周长为________;
(4)图③中,若∠A'GN=80°,则∠A'HD=________°;
(5)图③中的相似三角形(包括全等三角形)共有________ 对;
(6)如图④点A'落在边ND上,若 ,则 = ________(用含m,n的代数式表示).
答案解析部分
一、单选题
1. B
【解析】【解答】解: A:如果两个三角形相似,相似比为4:9,那么这两个三角形的周长比为4:9,故此答案错误,不符合题意;
B:如果两个三角形相似,相似比为4:9,那么这两个三角形的周长比为4:9, 故此答案正确,符合题意;
C:如果两个三角形相似,相似比为4:9,那么这两个三角形的面积比为16:81, 故此答案错误,不符合题意;
D:如果两个三角形相似,相似比为4:9,那么这两个三角形的面积比,14:81. 故此答案错误,不符合题意。
故答案为:B。
【分析】根据相似三角形周长的比等于相似比,面积的比等于相似比的平方,即可一一判断得出答案。
2. C
分析:解:∵△ABC∽△A'B'C',AD和A'D'是它们的对应中线,AD=10,A'D'=6,
∴△ABC与△A'B'C'的周长比=AD:A′D′=10:6=5:3.
故答案为:C.
【分析】根据相似三角形的周长之比、对应中线的比都等于相似比即可得出答案。
3. D
分析:解:∵ EM∥AD , EN∥AB
∴△DNE∽△DAB∽△EMB
∴
∵四边形ABCD是平行四边形
∴AD=BC
∴
故答案为:D
【分析】利用已知条件易证△DNE∽△DAB∽△EMB,利用相似三角形的性质,可证得, 再根据平行四边形的性质,可证得一定正确的结论。
4. B
分析:解:∵DE∥BC,
∴△ADE∽△ABC,
∴ = ,
即 = ,
解得:BC=6。
故答案为:B。
【分析】根据平行于三角形一边的直线截其它两边,所截的三角形原三角形相似得出△ADE∽△ABC,根据相似三角形对应边成比例得出 = ,根据比例式即可算出BC的长。
5. D
分析:解:设AF=k,则AC=3k,FC=2k, EF∥BC,则∠AEF=∠EBD,∴Rt△AEF∽Rt△EBD,AF:EF=ED:BD,
k:2k=2k:BD,∴BD=4k, BC=6k,由勾股定理得:AB2=AC2+BC2 ,AB2=15k2=300, ∴k2=20cm2, 所以S△ABC-S正方形CDEF=S△AEF+S△BDE=(4k×2k+2k×k)÷2=5k2=100cm2
故答案为:D
【分析】设AF=k, 根据三角形相似,把各边用k表示,统一量,在△ABC中利用勾股定理列式求出k2的值,把剩余部分的面积用k来表示,最后代入k2的值即可。
6. C
分析:∵ , ,
∴ ,
∴ ,即 ,
解得, 的面积为 ,
∴ 的面积为: ,
故答案为:C.
【分析】根据两角分别相等可证△ACD∽△BCA,利用相似三角形的面积比等于相似比的平方可得S△BCA=4S△ACD=4a,从而求出△ABD的面积.
二、填空题
7. 12+8
分析:解:连接AC交BD于K,
根据菱形的性质OA和HG互相垂直平分,又∵∠AOB=90°得HG∥KO,又OG∥KH,∴则四边形HKOG为平行四边形,则OK=HG=2。∠CDB+∠HDB=∠ADH+∠HDB=90°。又OH=OC,则△HOC为等腰直角△,∠CHO=45°,∵HG=KO=2,∠BOC=∠CAO,∠OCK=∠ACK,∴△OCK=△ACK, ,则BE=2OA= ,AB= ,则△ABE周长为BE+2AB= 。
在故答案为: 。
【分析】利用四边形HKOG是平行四边形得KO=2,由△COH是等腰直角三角形,得各边之比确定,本题关键是抓住A、H、C三点共线,找三角形相似,利用相似比可求OA的长,OA求出,∵△ABE是等腰直角三角形,则其他各边可求,得其周长。
三、综合题
8. (1)解:由正方形PQMN得PN∥BC,
∴△APN∽△ABC.
∴ ,即.
解得PN=
(2)证明:推理:由画法可得∠QMN=∠PNM=∠PQM=∠Q'M'N'=90°,
∴四边形PQMN为矩形,MN∥M'N'.
∴△BN'M'∽△BNM.
∴
同理可得
∴
:M'N'=P'N',∴MN=PN
∴四边形PQMN为正方形。
(3)解:过N作NR⊥EM于点R,
∵NE=NM,
∴∠NEM=∠NME,
∴ER=RM= EM,
又∵∠EQM+∠EMQ=∠EMQ+∠EMN=90°,
∴∠EQM=∠EMN,
又∠QEM=∠NRM=90°,NM=QM,
∴△EQM≌△RMN(AAS)
∴EQ=RM,
∴EQ= EM,
∵∠QEM=90°,
∴∠BEQ+∠NEM=90°,
∴BEQ=∠EMB,
又∵∠EBM=∠QBE,
∴△BEQ∽△BME,
∴ ,
设BQ=x,则BE=2x,BM=4x,
∴QM=BM-BQ=3x=MN=NE,
∴BN=BE+NE=5x,
∴BN= NM=
【解析】【分析】(1)温故:利用正方形的性质易证PN∥BC,就可证得△PAN∽△ABC,再利用相似三角形的性质,得出对应边成比例,建立关于PN的方程,解方程求出PN的长。
(2)推理:根据画法易证四边形PQMN是矩形,可得到MN∥M'N',易证△BMN和△BM'N',再利用相似三角形的性质,得出对应边成比例,同理可证△P'BN'∽△PBN,得出对应边成比例,利用中间比及M'N'=P'N',可证MN=PN,然后利用一组邻边相等的矩形是正方形,可证得结论。
(3) 拓展: 过N作NR⊥EM于点R, 根据已知条件去证明 △EQM≌△RMN,利用全等三角形的性质,可证得 EQ=RM,即可得到 EQ= EM ,再证明 △BEQ∽△BME,利用相似三角形的性质,得出对应边成比例,设BQ=x,用含x的代数式分别表示出BE、BM、QM、BN, 然后根据 BN= NM,就可求出“波利亚线”BN的长、
9. (1)解:如图,过M分别作ME∥AB交BC于点E,MF∥BC交AB于点F,
则四边形BEMF是平行四边形
∵四边形ABCD是正方形,
∴∠ABC=90°,∠ABD=∠CBD=∠BME=45°
∴ME= BE
∴平行四边形MEBF是正方形.
∴ME=MF
∵CM⊥MN,
∴∠CMN=90°
∵∠FME=90°
∴.∠CME=∠FMN
∴△MFN≌△MEC,
∴MN=MC
(2)证明:由(1)得:FM∥AD,EM∥CD
.
AF=24.CE=24.
△MFN≌△MEC
∴FN=EC=2.4
N=4.8,BN=6-4.8=1.2
AN=4BN
(3)解:把△DMC绕点C逆时针旋转90°得到△BHC,连接GH
∵△DMC≌△BHC,∠BCD=90°,
∴MC=HC,DM=BH,∠CDM=∠CBH,∠DCM=∠BCH=45°
∴∠MBH=90°,∠MCH=90°
MC=MN,MC⊥MN
∴△MNC是等腰直角三角形
∠MNC=45°
∴∠NCH=45°
∴△MCG≌△HCG
∴MG=HG
∵BG:MG=3:5,
∴设BG=3a,则MG=GH=5a
在Rt△BGH中,BH= =4a,则MD=4a
∵正方形ABCD的边长为6,
.BD=6
∴DM+MG+BG=12a=6
∴a=
∴BG= ,MG=
∵∠MGC=∠NGB,∠MNG=∠GBC=45°
∴△MGC∽△MGB.
∴
∴CG·NG=BG·MG≈
【解析】【分析】(1)如图,过M分别作ME∥AB交BC于点E,MF∥BC交AB于点F,先证四边形MEBF是正方形,可得ME=MF,根据同角的余角相等可得∠CME=∠FMN,根据“ASA”可证△MFN≌△MEC,利用全等三角形的对应边相等可得MN=MC.
(2)根据平行线分线段成比例定理可得, 据此可得AF=24.CE=24,利用全等三角形对应边相等可得FN=EC=2.4,从而求出AN=4.8,BN=6-4.8=1.2,据此得出结论.
(3)把△DMC绕点C逆时针旋转90°得到△BHC,连接GH,根据旋转的性质可得△MNC是等腰直角三角形,可得∠NCH=45°,根据“SAS”可证△MCG≌△HCG,可得MG=HG. 设BG=3a,则MG=GH=5a, 在Rt△BGH中,利用勾股定理求出BH的长,从而可得MD.利用正方形的性质可得BD=, 由DM+MG+BG=12a=6 , 求出a值,从而求出BG、MG的长.根据两角分别相等可证 △MGC∽△MGB,可得 , 继而得出结论.
10. (1)75;4-2
(2)解:△AND等边三角形
证明:由折叠可知DN=CD=AD
∵DE= AD∴DE= DN
∵EF⊥AD∴∠END=30°
∴∠ADN=60°
∴△ADN是等边三角形
(3)12
(4)40
(5)4
(6)
【解析】【分析】(1)根据折叠角和折叠边都相等,写出即可。
(2)根据折叠的性质,折叠边相等, 可判断三角形为等边三角形。
(3)根据图中的信息,利用周长公式,求得即可。
(4)根据角度关系的换算,可得出角的度数。
(5)根据全等三角形和相似三角形的判定定理可得出个数。
(6)根据题意,用m、n表示出线段的比即可。
初中数学华师大版九年级上册3. 相似三角形的性质优秀课时训练: 这是一份初中数学华师大版九年级上册3. 相似三角形的性质优秀课时训练,共29页。试卷主要包含了0分),【答案】D,【答案】C,【答案】B,【答案】A等内容,欢迎下载使用。
华师大版2.频率与概率课后作业题: 这是一份华师大版2.频率与概率课后作业题,共5页。试卷主要包含了单选题,填空题,综合题等内容,欢迎下载使用。
数学九年级上册24.1 测量同步测试题: 这是一份数学九年级上册24.1 测量同步测试题,共8页。试卷主要包含了单选题,填空题,解答题,综合题等内容,欢迎下载使用。













