初中数学华师大版九年级上册4. 相似三角形的应用课后练习题
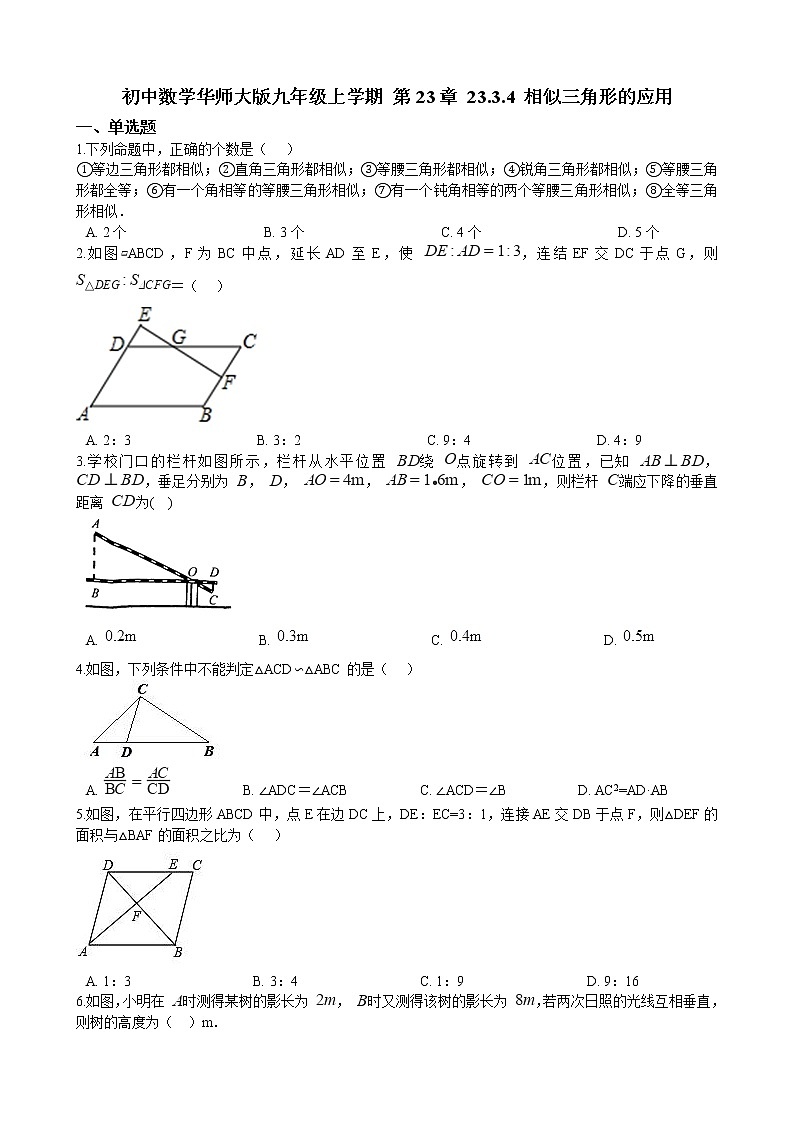
展开1.下列命题中,正确的个数是( )
①等边三角形都相似;②直角三角形都相似;③等腰三角形都相似;④锐角三角形都相似;⑤等腰三角形都全等;⑥有一个角相等的等腰三角形相似;⑦有一个钝角相等的两个等腰三角形相似;⑧全等三角形相似.
A. 2个 B. 3个 C. 4个 D. 5个
2.如图▱ABCD,F为BC中点,延长AD至E,使 ,连结EF交DC于点G,则 =( )
A. 2:3 B. 3:2 C. 9:4 D. 4:9
3.学校门口的栏杆如图所示,栏杆从水平位置 绕 点旋转到 位置,已知 , ,垂足分别为 , , , , ,则栏杆 端应下降的垂直距离 为( )
A. B. C. D.
4.如图,下列条件中不能判定△ACD∽△ABC的是( )
A. B. ∠ADC=∠ACB C. ∠ACD=∠B D. AC2=AD·AB
5.如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交DB于点F,则△DEF的面积与△BAF的面积之比为( )
A. 1:3 B. 3:4 C. 1:9 D. 9:16
6.如图,小明在 时测得某树的影长为 , 时又测得该树的影长为 ,若两次日照的光线互相垂直,则树的高度为( )m.
A. 2 B. 4 C. 6 D. 8
二、填空题
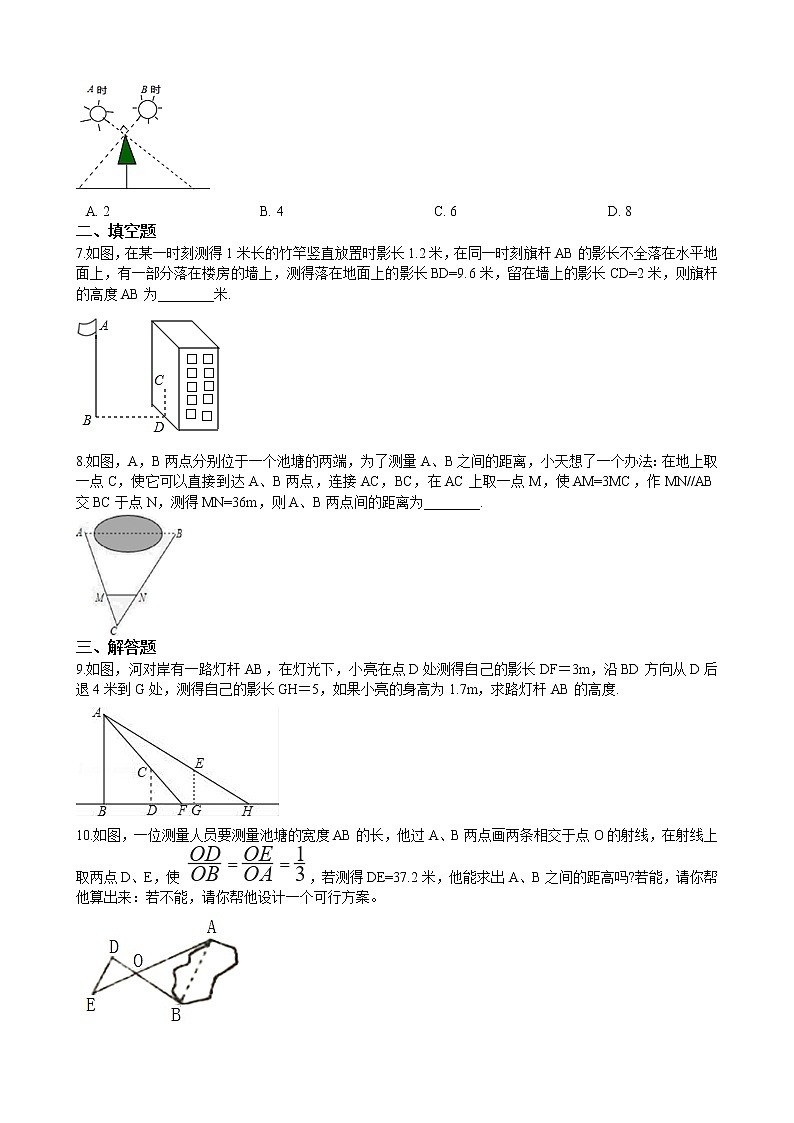
7.如图,在某一时刻测得1米长的竹竿竖直放置时影长1.2米,在同一时刻旗杆AB的影长不全落在水平地面上,有一部分落在楼房的墙上,测得落在地面上的影长BD=9.6米,留在墙上的影长CD=2米,则旗杆的高度AB为________米.
8.如图,A,B两点分别位于一个池塘的两端,为了测量A、B之间的距离,小天想了一个办法:在地上取一点C,使它可以直接到达A、B两点,连接AC,BC,在AC上取一点M,使AM=3MC,作MN//AB交BC于点N,测得MN=36m,则A、B两点间的距离为________.
三、解答题
9.如图,河对岸有一路灯杆AB,在灯光下,小亮在点D处测得自己的影长DF=3m,沿BD方向从D后退4米到G处,测得自己的影长GH=5,如果小亮的身高为1.7m,求路灯杆AB的高度.
10.如图,一位测量人员要测量池塘的宽度AB的长,他过A、B两点画两条相交于点O的射线,在射线上取两点D、E,使 ,若测得DE=37.2米,他能求出A、B之间的距高吗?若能,请你帮他算出来:若不能,请你帮他设计一个可行方案。
11.如图,在△ABC中,AB=4cm,BC=8cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,经几秒后,点P、B、Q构成的三角形△PBQ与△ABC相似?
四、综合题
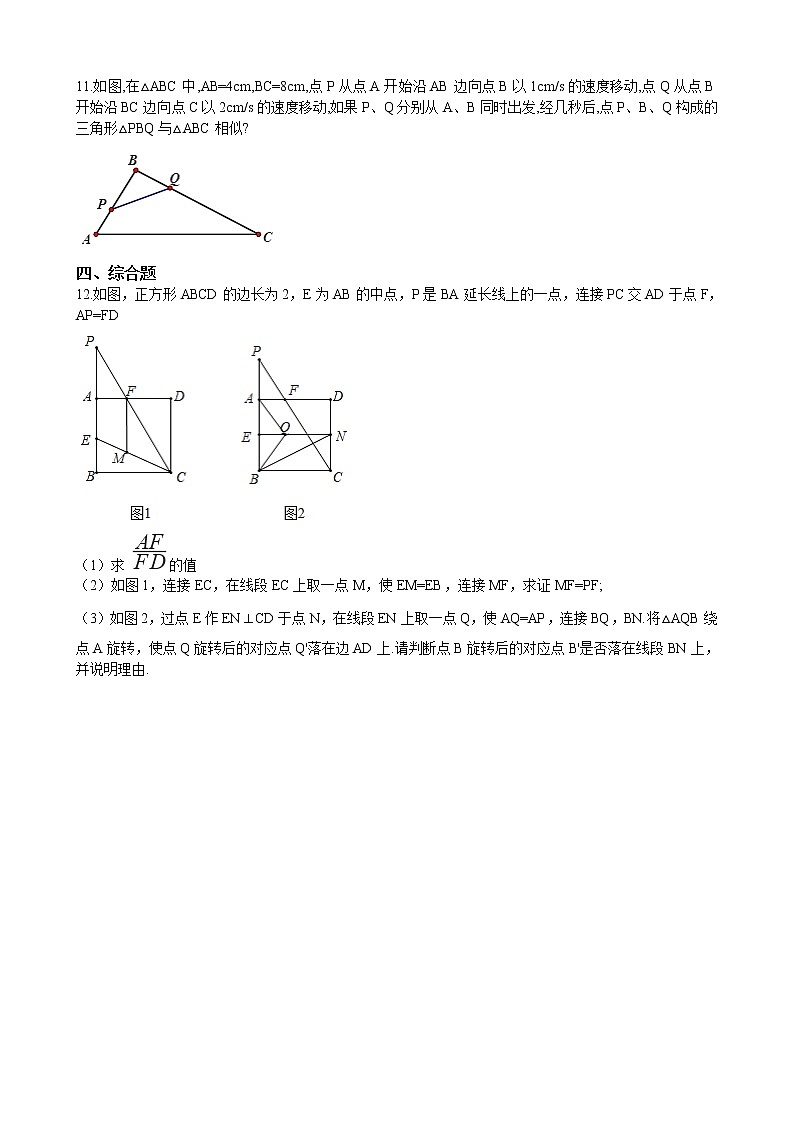
12.如图,正方形ABCD的边长为2,E为AB的中点,P是BA延长线上的一点,连接PC交AD于点F,AP=FD
(1)求 的值
(2)如图1,连接EC,在线段EC上取一点M,使EM=EB,连接MF,求证MF=PF;
(3)如图2,过点E作EN⊥CD于点N,在线段EN上取一点Q,使AQ=AP,连接BQ,BN.将△AQB绕点A旋转,使点Q旋转后的对应点Q'落在边AD上.请判断点B旋转后的对应点B'是否落在线段BN上,并说明理由.
答案解析部分
一、单选题
1. B
分析:解:①∵等边三角形的各角都是60°,∴等边三角形都相似;①正确;
②∵直角三角形的直角相等,但两个锐角不一定相等,∴直角三角形不一定相似;②错误;
③∵等腰三角形的顶角不一定相等,则底角也不一定相等,∴等腰三角形不一定相似;③错误;
④锐角三角形不一定都相似,④错误;
⑤等腰三角形不一定都全等; ⑤错误;
⑥有一个角相等的等腰三角形相似不一定相似:如30°,30°,120°的等腰三角形和30°,75°,75°的两个等腰三角形就不相似;⑥错误;
⑦有一个钝角相等的两个等腰三角形相似;因为钝角只能是顶角,所以底角也相等,所以相似,⑦正确;
⑧∵全等三角形是相似比等于1的情况,属于相似;∴全等三角形都相似.⑧正确.
综上,正确的结论有3个.
故答案为:B
【分析】根据相似三角形对应边成比例,对应角相等,进行选项的判定。所以①⑦⑧满足判定条件,正确。
2. D
分析:解:设 ,
∵ ,
∴ ,
∵四边形ABCD是平行四边形,
∴ , ,
∵点F是BC的中点,
∴ ,
∵ ,
∴ ,
∴ ,
故答案为:D.
【分析】设 ,仔细审题再结合平行四边形的性质可将CF表示出来,再根据相似三角形的判定易证 , 由相似三角形的性质中相似三角形面积的比等于相似比的平方,可求出结论
3. C
分析:∵ , ,
∴AB∥CD
∴△AOB∽△COD,
∴
∵AO=4m ,AB=1.6m ,CO=1m,
∴ .
故答案为:C.
【分析】根据同一平面内垂直于同一直线的两条直线互相平行得出AB∥CD,根据平行于三角形一边的直线截其它两边的延长线,所截得的三角形与原三角形相似得出△AOB∽△COD,根据相似三角形对应边成比例得出, 根据比例式即可算出CD的长。
4. A
分析:解:根据两角对应相等的两三角形相似,可知B、C均可以判定两三角形相似;根据两边对应成比例且夹角相等,可由AC2=AD·AB,∠A为公共角,可判定两三角形相似.
故答案为:A.
【分析】根据两个角相等的三角形相似,可推出B和C选项正确;根据三角形对应边成比例,且夹角相同,可证明D选项正确,所以A选项错误。
5. D
分析:解:∵四边形ABCD为平行四边形,
∴DC∥AB,
∴△DFE∽△BFA,
∵DE:EC=3:1,
∴DE:DC=3:4,
∴DE:AB=3:4,
∴S△DFE:S△BFA=9:16,
故答案为:D.
【分析】根据题意,易证△DFE∽△BFA,所以相似三角形对应边成比例,面积的比等于对应比的平方,即可求出正确答案。
6. B
分析:解:根据题意,作△EFC;
树高为CD,且∠ECF=90°,ED=2,FD=8;
∵∠E+∠ECD=∠E+∠CFD=90°
∴∠ECD=∠CFD
∴Rt△EDC∽Rt△FDC,
有 ;即DC2=ED•FD,
代入数据可得DC2=16,
DC=4;
故答案为:B.
【分析】根据“两角对应相等,两个三角形相似”判定Rt△EDC∽Rt△FDC,再根据相似三角形性质可得=,代入数据求得DC。
二、填空题
7. 10
分析:解:如图,
过点C作CE⊥AB于点E,可得四边形BDCE为矩形,
∴CE=CE=9.6米,BE=CD=2米,
由题意可得:,
∴AE=8(米),
∴AB=AE+BE=8+2=10(米).
故答案为:10.
【分析】根据三个角是直角的四边形是矩形,可得四边形BDCE为矩形,利用矩形的对边相等,可得CE=CE=9.6米,BE=CD=2米,利用“在同一时刻物高与影长的比相等”,可得, 从而求出AE的长,继而求出AB的长.
8. 144m
分析:解:∵MN∥AB,
∴△CMN∽△CAB,
∴ ,
∵AM=3MC,MN=36m,
∴ ,
AB=144m,
故答案为:144m.
【分析】利用MN∥AB可判定△CMN∽△CAB,然后利用相似三角形的相似比即可求解。
三、解答题
9. 解:∵CD⊥BF,AB⊥BF,
∴CD∥AB,
∴△CDF∽△ABF,
∴ = ,
同理可得 = ,
∴ = ,
∴ = ,
解得BD=6,
∴ = ,
解得AB=5.1.
答:路灯杆AB高5.1m.
【解析】【分析】根据垂直于同一条直线的两条直线平行可得CD∥AB, 由平行于三角形一边的直线截其它两边,所构成的三角形与原三角形相似可得△CDF∽△ABF, 利用相似三角形的对应边成比例可得= ,同理可得 = ,利用等量代换求出= ,把已知条件代入求出BD=6, 再根据 = 即可求路灯杆AB的高度.
10. 解:∵, ∠DOE=∠BOA,
∴△DOE∽△BOA,
∴,
∵ DE=37.2
∴,
∴AB=111.6.
答: A、B之间的距离为111.6米.
【解析】【分析】先根据两边成比例且夹角相等的两个三角形相似,可证△DOE∽△BOA,利用相似三角形的对应边成比例可得, 从而求出AB的长,从而得出答案.
11. 解:设经过t秒后,△PBQ与△ABC相似,
∵点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,
∴AP=t,BQ=2t,
∵AB=4,BC=8,
∴BP=AB-AP=4-t,
①当△PBQ∽△ABC时,
∴,
即,
解得:t=2;
②当△PBQ∽△CBA时,
∴,
即,
解得:t=;
综上所述:经过2秒或秒,△PBQ与△ABC相似.
【解析】【分析】根据题意可得AP=t,BQ=2t,BP=4-t,分情况讨论:①当△PBQ∽△ABC时,②当△PBQ∽△CBA时,根据相似三角形的性质分别列出方程,解之即可得出答案.
四、综合题
12. (1)解:设AP=x,则FD=x,AF=2-x
∵在正方形ABCD中,AB∥CD
∴
∴
∴.x2=4-2x
x2+2x-4=0
=20
∵x>0
∴x=
∴
(2)解:连接OP
∵PA=DF,AD=DC,∠PAD=∠ADC
∴ PAD≌ FDC
又∵EC= BE=ME= AB=1
∴MC= =FD
又∵PE=AP+AE= +1= =EC
∴∠EPC=∠ECP
又∵AB∥CD
∴∠EPC=∠DCF
∴∠PDA=∠ECP
∴ PFD∽ FMC(SAS)
∴MF=PF
(3)解:如图,在AD上取一点Q',使AQ'=AQ,在BN上取一点B',AB'=AB,连接B'Q',做B'G⊥AD交EN于点K,交AD于点G
∵tan∠NBE=2,AB=AB'=2
∴BB'=
∴B'N=BN=BB'= "ANB'KOANBE
∵ NB'K~ NBE
∴B'K= ;KN= ;
∴B'G= ;DG=
∴Q'G=3- - =
在Rt B'GQ'中,∠B'GQ'=90°,有B'Q=
而( -1)2≠
∴B'Q'≠( -1)2
∴B'Q'≠BQ,点B'不在BN上
【解析】【分析】(1)设AP=x,则FD=x,AF=2-x,由正方形性质得AB∥CD,再由平行线截线段成比例得 ,即 ,解之得x= -1,将x值代入 即可得 的值.(2)连结DP,根据全等三角形判定SAS得△PAD≌△FDC,由全等三角形性质得PA=FD= -1,在Rt△BEC中,由勾股定理求得EC长,从而可得MC=FD,由相似三角形判定得△PFD∽△FMC,根据相似三角形性质得 =1,由此可得PF=FM.(3)在AD上取一点Q´,使AQ´=AQ,在BN上取一点B´,AB´=AB,连结B´Q´,作B´G⊥AD交EN于点K,交AD于点G,根据锐角三角函数正切定义求得BB´=BN=B´N长,由相似三角形的性质求得B´K,KN,从而可得B´G,DG,Q´G长,在Rt△B´GQ´中,根据勾股定理求得B´Q´= ,而( -1)2≠ ,即B´Q´≠( -1)2 , 从而可得点B´不在BN上.
初中数学华师大版九年级上册4. 相似三角形的应用课后练习题: 这是一份初中数学华师大版九年级上册4. 相似三角形的应用课后练习题,文件包含相似三角形的应用-九年级数学上册尖子生同步培优题典解析版华师大版docx、相似三角形的应用-九年级数学上册尖子生同步培优题典原卷版华师大版docx等2份试卷配套教学资源,其中试卷共95页, 欢迎下载使用。
华师大版九年级上册4. 相似三角形的应用精品一课一练: 这是一份华师大版九年级上册4. 相似三角形的应用精品一课一练,共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
数学九年级上册第23章 图形的相似23.3 相似三角形4. 相似三角形的应用精品课时训练: 这是一份数学九年级上册第23章 图形的相似23.3 相似三角形4. 相似三角形的应用精品课时训练,共15页。试卷主要包含了0分),【答案】D,【答案】A,【答案】C,【答案】165,【答案】720等内容,欢迎下载使用。













