初中人教版14.1.1 同底数幂的乘法教案及反思

这是一份初中人教版14.1.1 同底数幂的乘法教案及反思，共6页。教案主要包含了提出问题，创设情境，探究问题，形成概念，练习巩固，小结与作业等内容，欢迎下载使用。
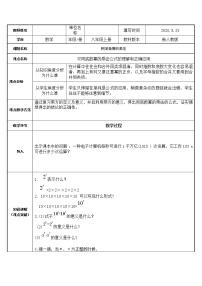
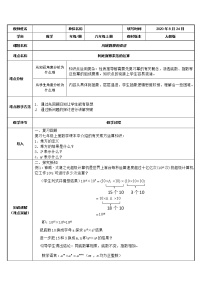
 学科数学年级/册八年级教材版本人教版课题名称第十四章 整式的乘法与因式分解14.1.1  同底数幂的乘法 教学目标理解同底数幂的乘法法则,运用同底数幂的乘法法则解决一些实际问题重难点分析重点分析同底数幂的乘法是建立在七年级上册单项式与多项式基础知识上，如果学生没有很好掌握七年级上册单项式与多项式的概念，那么同底数幂的乘法就不太好掌握。难点分析学生抽象逻辑思维较弱，不能够很好的从具体数字到字母的一个抽象化转变的过程，所以在学习过程中会有一定的难度。 教学方法 1.本课的主要教学任务是“同底数幂乘法的运算性质”：同底数幂相乘，底数不变，指数相加. 在课堂教学时，通过幂的意义引导学生得出这一性质，接着再引导学生深入探讨同底数幂运算，幂的底数可以是“任意有理数、单项式、多项式”，训练学生的整体思想． 教学环节教学过程新课导入一、提出问题，创设情境复习an的意义：an表示n个a相乘，我们把这种运算叫做乘方，乘方的结果叫做幂；a叫做底数，n是指数．(出示投影片 )                          知识讲解（难点突破）二、探究问题，形成概念(出示投影片）提出问题：(出示投影片)问提出问题：(出示投影片)问题：一种电子计算机每秒可进行1千万亿(1015)次运算，它工作103秒可进行多少次运算？[师]能否用我们学过的知识来解决这个问题呢？[生]运算次数＝运算速度×工作时间，所以计算机工作103秒可进行的运算次数为：1015×103.[师]1015×103如何计算呢？[生]根据乘方的意义可知1015×103＝(10×10×…×10)15个10×(10×10×10)＝(10×10×…×10)18个10＝1018.你发现了什么？注意观察计算前后底数和指数的关系，并能用自己的语言描述．[师]根据乘方的意义，同学们可以独立解决上述问题．[生](1)25×22＝(2×2×2×2×2)×(2×2)＝27＝25＋2.因为25表示5个2相乘，22表示2个2相乘，根据乘方的意义，同样道理可得a3·a2＝(a·a·a)(a·a)＝a5＝a3＋2.5m·5n＝(5×5·…·5),\(m个5))×(5×5·…·5),\（n个5))＝5m＋n.[生]我们可以发现下列规律：am·an等于什么(m，n都是正整数)？为什么？(1)这三个式子都是底数相同的幂相乘；(2)相乘结果的底数与原来底数相同，指数是原来两个幂的指数的和．2．议一议(出示投影片)[师生共析]am·an表示同底数幂的乘法．根据幂的意义可得：am·an＝(a×a·…·a)m个a·(a×a·…·a)n个a＝a·a·…·a(m＋n)个a＝am＋n于是有am·an＝am＋n(m，n都是正整数)，用语言来描述此法则即为：“同底数幂相乘，底数不变，指数相加”．[师]请同学们用自己的语言解释“同底数幂相乘，底数不变，指数相加”的道理，深刻理解同底数幂的乘法法则．[生]am表示m个a相乘，an表示n个a相乘，am·an表示m个a相乘再乘以n个a相乘，也就是说有(m＋n)个a相乘，根据乘方的意义可得am·an＝am＋n.[师]也就是说同底数幂相乘，底数不变，指数要降一级运算，变为相加    课堂练习（难点巩固）三、练习巩固典例精析出示投影片例1 计算：(1)x2·x5=__________________;（2）a·a6=__________________;（3）xm·x3m+1=__________________;（4）a·a6·a3=__________________;[例2]计算am·an·ap后，能找到什么规律？[师]我们先来看例1，是不是可以用同底数幂的乘法法则呢？[生1](1)，(2)，(4)可以直接用“ 同底数幂相乘，底数不变，指数相加”的法则．[生2](3)也可以，先算两个同底数幂相乘，将其结果再与第三个幂相乘，仍是同底数幂相乘，再用法则运算就可以了．[师]同学们分析得很好．请自己做一遍．每组出一名同学板演，看谁算得又准又快．生板演：(1)解：x2·x5＝x2＋5＝x7；(2)解：a·a6＝a1·a6＝a1＋6＝a7；(3)解：2×24×23＝21＋4·23＝25·23＝25＋3＝28；(4)解：xm·x3m＋1＝xm＋(3m＋1)＝x4m＋1.[师]接下来我们来看例2.受(3)的启发，能自己解决吗？与同伴交流一下解题方法．解法一：am·an·ap＝(am·an)·ap＝am＋n·ap＝am＋n＋p；解法二：：am·an·ap＝am·(an·ap)＝am·an＋p＝am＋n＋p；解法三：am·an·ap＝(a·a…a)m个a·(a·a…a)n个a·(a·a…a)p个a＝am＋n＋p归纳：解法一与解法二都直接应用了运算法则，同时还运用了乘法的结合律；解法三是直接应用乘方的意义．三种解法得出了同一结果．我们需要这种开拓思维的创新精神．[生]那我们就可以推断，不管是多少个幂相乘，只要是同底数幂相乘，就一定是底数不变，指数相加．[师]是的，能不能用符号表示出来呢？[生]am1·am2·am3·…amn＝am1＋m2＋m3＋…mn.[师]鼓励学生．那么例1中的第(3)题我们就可以直接应用法则运算了．2×24×23＝21＋4＋3＝28.三、随堂练习1．m14可以写成(　　)A．m7＋m7  B．m7·m7C．m2·m7  D．m·m142．若xm＝2，xn＝5，则xm＋n的值为(　　)A．7  B．10  C．25  D．523．计算：－22×(－2)2＝________；(－x)(－x2)(－x3)(－x4)＝________．4．计算：(1)(－3)2×(－3)5；(2)106·105·10；(3)x2·(－x)5；(4)(a＋b)2·(a＋b)6.   小结四、小结与作业小结：谈谈本节课的收获．[师]这节课我们学习了同底数幂的乘法的运算性质，请同学们谈一下有何新的收获和体会呢？[生]在探索同底数幂乘法的性质时，进一步体会了幂的意义，了解了同底数幂乘法的运算性质．[生]同底数幂的乘法的运算性质是底数不变，指数相加．应用这个性质时，我觉得应注意两点：一是必须是同底数幂的乘法才能运用这个性质；二是运用这个性质计算时一定是底数不变，指数相加，即am·an＝am＋n(m，n是正整数)．五、课后作业教材第96页练习1.2．