初中数学人教版七年级上册3.1.1 一元一次方程精品练习题习题课件ppt

这是一份初中数学人教版七年级上册3.1.1 一元一次方程精品练习题习题课件ppt，文件包含341利用一元一次方程解配套问题和工程问题课件pptx、341实际问题与一元一次方程1课后练习doc、341用一元一次方程解配套问题和工程问题教学设计教案docx等3份课件配套教学资源，其中PPT共34页， 欢迎下载使用。
解下面方程，并说一说解一元一次方程的一般步骤：
去分母（方程两边乘12），得
列方程解应用题的一般步骤： 设未知数、列方程、解方程、检验所得结果、确定答案；可简要地概括为“设、列、解、检、答”．
小学学过的列方程解应用题的步骤有哪些？
观察下图中出现成套使用的物品，试着发现生活中其他相似的例子。
今天我们一起探讨一下数学中这样的配套问题。
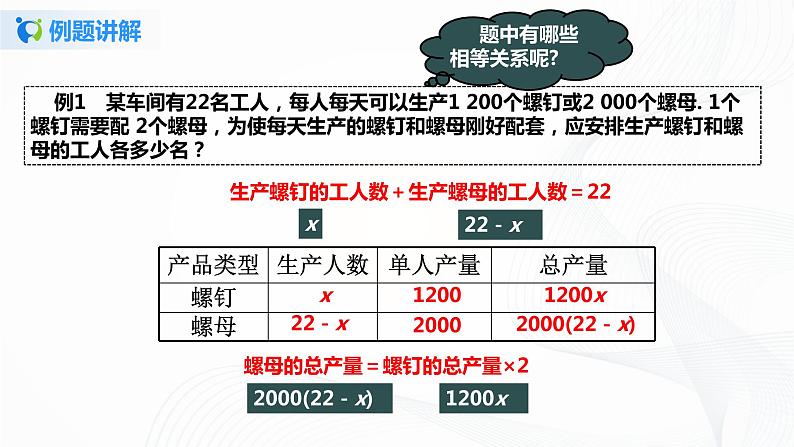
例1　某车间有22名工人，每人每天可以生产1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺母，为使每天生产的螺钉和螺母刚好配套，应安排生产螺钉和螺母的工人各多少名？
题中有哪些相等关系呢?
螺母的总产量＝螺钉的总产量×2
生产螺钉的工人数＋生产螺母的工人数＝22
解：设应安排x名工人生产螺钉，(22－x)名工人生产螺母，根据题意可列方程： 2 000(22－x)＝2×1 200x . 解得： x＝10. ∴ 22－x＝12.答：应安排10名工人生产螺钉，12名工人生产螺母.
配套问题解题思路： 1.利用配套问题中物品之间具有的数量关系作为列方程的依据； 2.利用配套问题中的套数不变作为列方程的依据．
练一练：1.学校购买40套课桌椅(一把椅子配一张桌子),总价为2800元,若每把椅子20元,则每张桌子多少元？设每张桌子x元,可列方程为( )A.40x+20=2800B.40x+40×20=2800C.40(x-20)=2800D.40x+20(40-x)=2800
2. 用铝片做听装饮料瓶，现有100张铝片，每张铝片可制瓶身16个或制瓶底45个，一个瓶身和两个瓶底可配成一套.设用x张铝片制瓶身，则下面所列方程正确的是(　　)A. 2×16x＝45(100－x) B. 16x＝45(100－x)C. 16x＝2×45(100－x) D. 16x＝45(50－x)
例2 整理一批图书，由一个人做要 40 h 完成. 现计划由一部分人先做 4 h，然后增加 2人与他们一起做8 h，完成这项工作. 假设这些人的工作效率相同，具体应先安排多少人工作？
提示：在工程问题中：工作量=人均效率×人数×时间；前一部分工作量＋后一部分工作量＝“1”
解：设先安排 x 人做4 h，
4x+8（x+2）＝40
4x+8x+16＝40
答：应先安排 2人做4 小时.
一项工作,甲队单独做要12天完成,乙队单独做要8天完成.现甲队先做3天后,乙队来支援,那么两队合做几天后完成这项工作的三分之二？
答：两队合做2天后完成任务的三分之二.
解：设两队合做x天后完成任务的三分之二,则
某工程甲单独完成要45天，乙单独完成要30天，若乙先单独干22天，剩下的由甲单独完成．问甲、乙一共用几天可以完成全部工作？若设甲、乙共用x天完成，则符合题意的方程是( )
一水池装有甲、乙、丙三个水管，甲、乙两管是注水管，丙管是排水管，单独开甲管6小时可注满水池，单独开乙管8小时可注满水池，单独开丙管12小时可把满水池的水排完．现在先打开甲、乙两管进水2小时，再打开丙管．问打开丙管几小时后便可将水池注满水？
解：设打开丙管x小时后便可将水池注满水，根据题意可列方程：
答：打开丙管2小时后便可将水池注满水.
工程问题解题思路：1. 1÷完成任务所需天数=每天完成这项任务的几分之一；2. 实际工作天数×每天完成这项任务的几分之一=实际完成这项工作的几分之几.
一元一次方程解决实际问题的基本过程如下：
一元一次方程的解 (x=a)
要点1　利用一元一次方程解配套问题1. 列一元一次方程解决实际问题的一般步骤是：分析问题中的 关系、设未知数、列方程、 、检验并写出答案.2. 产品配套问题的特点是“几个A配几个B”或“某个部件由几个A和几个B组成”等，题目的配套关系是列方程时的一个 关系.
要点1　1. 等量 解方程 2. 等量
要点2　利用一元一次方程解工程问题解决工程问题时，常把工作总量看成单位“ ”，基本关系式是：工作量＝ ×工作时间，相等关系是：各部分工作量的和＝ .
要点2　1 工作效率 工作总量
今天我们学习了哪些知识？
1.如何用一元一次方程解决实际问题？ 2.用一元一次方程解决实际问题一般包括哪些步骤.
1. 制一张桌子要用一个桌面和4条桌腿，1立方米木材可制作20个桌面，或者制作400条桌腿.现有12立方米木材，应安排多少立方米木材制作桌面才能使桌子配套(　　)A. 2　　 B. 6　　 C. 8　　 D. 10
2.八年级(1)班学生参加绿化劳动，在甲处有32人，乙处有22人，现根据需要，要从乙处抽调部分同学前往甲处，使甲处人数是乙处人数的2倍，问应从乙处抽调多少人前往甲处？设从乙处抽调x人前往甲处，可得正确方程是( ) A.32－x＝2(22－x) B.32＋x＝2(22＋x) C.32－x＝2(22＋x) D.32＋x＝2(22－x)
3. 某工厂男、女工人共70人，男工人调走10%，女工人调入6人，男、女工人数正好相等，则原来男、女工人数分别有(　　)40人，30人 B. 30人，40人 C. 35人，35人 D. 43人，27人
4.某工程甲单独完成要45天，乙单独完成要30天，若乙先单独干22天，剩下的由甲单独完成．问甲、乙一共用几天可以完成全部工作？若设甲、乙共用x天完成，则符合题意的方程是( )
5．教室里有40套课桌椅(一把椅子配一张桌子)，总价值2800元，每把椅子20元，则每张桌子多少元？设每张桌子x元，可列方程为( ) A.40x＋20＝2800 B.40x＋40×20＝2800 C.40(x－20)＝2800 D.40x＋20(40－x)＝2800
6. 某地为了打造风光带，将一段长为360m的河道整治任务交给甲、乙两个工程队先后接力完成，共用时20天，已知甲工程队每天整治24m，乙工程队每天整治16m，求甲、乙两个工程队分别整治了多长的河道.
7. 在手工制作课上，老师组织七年级(2)班的学生用硬纸制作圆柱形茶叶筒.七年级(2)班共有学生44人，其中男生人数比女生人数少2人，并且每名学生每小时剪筒身50个或剪筒底120个.(1)七年级(2)班有男生、女生各多少人？(2)要求一个筒身配两个筒底，为了使每小时剪出的筒身与筒底刚好配套，应该分配多少名学生剪筒身，多少名学生剪筒底？
解：(1)设七年级(2)班有女生x人，则男生(x－2)人，由题意，得x＋(x－2)＝44，解得x＝23，x－2＝21.　答：七年级(2)班有女生23人，男生21人.　(2)设分配a名学生剪筒身，则剪筒底的学生有(44－a)名由题意，得50a×2＝120(44－a)，解得a＝24，44－a＝20.　答：分配24名学生剪筒身，20名学生剪筒底.
8.一套仪器由一个A部件和三个B部件构成. 用1 m3钢材可以做40个A部件或240个B部件. 现要用6 m3钢材制作这种仪器，应用多少钢材做A部件，多少钢材做B部件，恰好配成这种仪器多少套？
解：设应用 x m3钢材做A部件，(6－x) m3 钢材做B部件. 依题意得： 3×40 x＝240 (6－x) . 解得： x＝4. 答：应用4 m3钢材做A部件，2 m3 钢材做B部件,配成这种仪器160套
9.一条地下管线由甲工程队单独铺设需要12天，由乙工程队单独铺设需要24天. 如果由这两个工程队从两端同时施工，要多少天可以铺好这条管线？
实际问题与一元一次方程
2.利用配套问题中的套数不变作为列方程的依据．
1.利用配套问题中物品之间具有的数量关系作为列方程的依据；
实际工作天数×每天完成这项任务的几分之一=实际完成这项工作的几分之几.
1÷完成任务所需天数=每天完成这项任务的几分之一；
数学问题(一元一次方程)
数学问题的解(一元一次方程的解)x＝a
解决实际问题的基本过程：